[Python] 실행 시간 측정하기 (measuring elapsed time in Python)
Python 분석과 프로그래밍/Python 데이터 전처리 2021. 11. 17. 20:58프로그래밍 코드를 짜다보면 수행 절차나 방법, 사용하는 메소드에 따라서 수행 시간이 차이가 나는 경우가 종종 있습니다. 그리고 성능이 중요해서 여러가지 방법을 테스트해보면서 가장 실행시간이 짧도록 튜닝하면서 최적화하기도 합니다.
이번 포스팅에서는 Python에서 코드를 실행시켰을 때 소요된 시간을 측정하는 2가지 방법을 소개하겠습니다.
(1) datetime.now() 메소드 이용해서 실행 시간 측정하기
(2) %timeit 로 실행 시간 측정하기

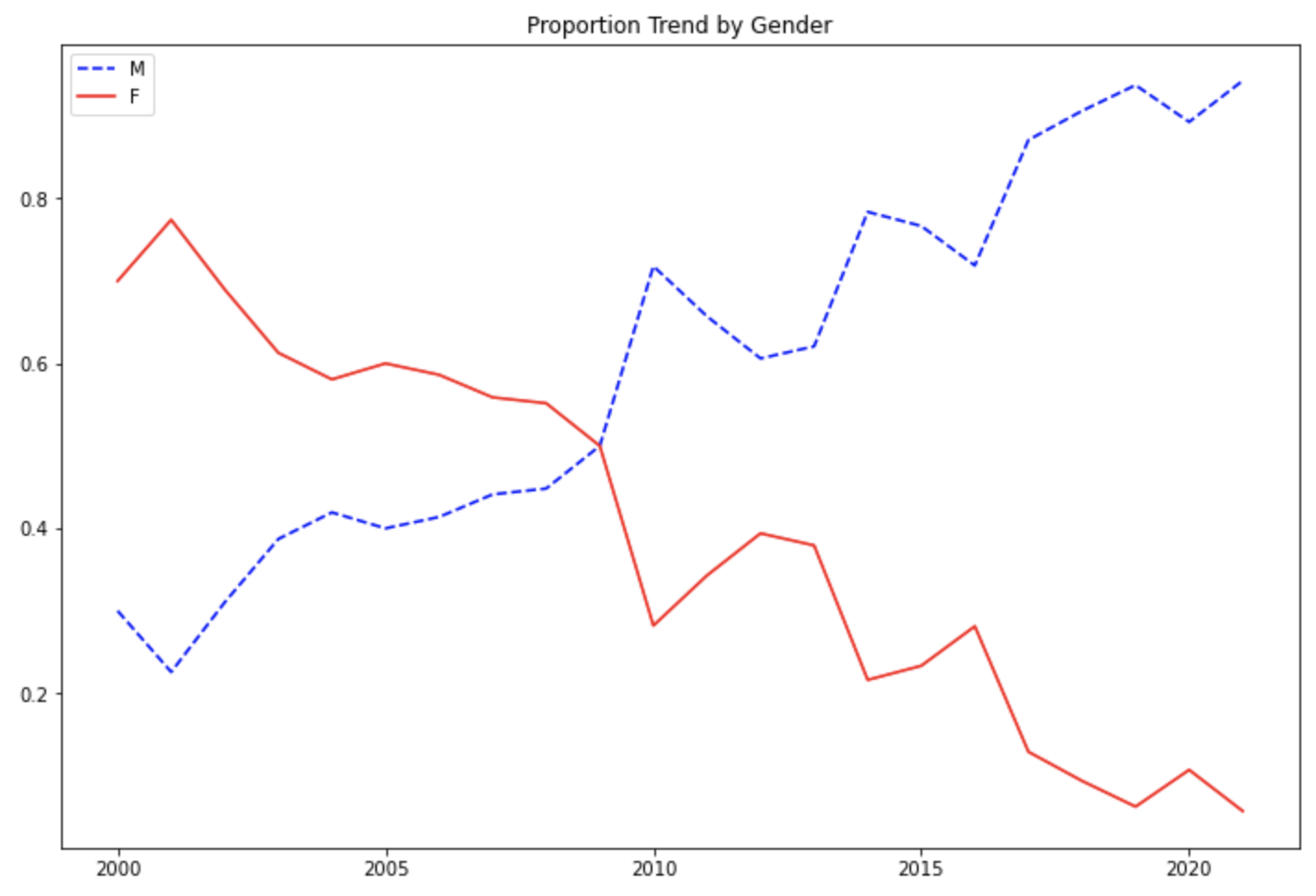
먼저, 예제로 사용할 샘플 데이터셋으로서, 1억개의 값을 가지는 xarr, yarr 의 두개의 배열(array)를 만들어 보겠습니다. 그리고 배열 내 각 1억개의 값 별로 True/False 의 조건값을 가지는 cond 라는 배열도 난수를 생성시켜서 만들어보겠습니다.
import numpy as np
## generating sample array with 100 million values
xarr = np.arange(100000000)
yarr = np.zeros(100000000)
cond = np.where(np.random.randn(100000000)>0, True, False)
cond[:10]
# [Out] array([False, True, True, False, False, True, True, True,
# True, True])
위에서 만든 1억개의 원소를 가지는 배열을 가지고 조건값으로 True/False 블리언 값 여부에 따라서 True 조건값 이면 xarr 배열 내 값을 가지고, False 조건값이면 yarr 배열 내 값을 가지는 새로운 배열을 만들어보겠습니다. 이때 (1) List Comprehension 방법과, (2) NumPy의 Vectorized Operations 방법 간 수행 시간을 측정해서 어떤 방법이 더 빠른지 성능을 비교해보겠습니다.
(물론, Vectorized Operations이 for loop 순환문을 사용하는 List Comprehension보다 훨~씬 빠릅니다! 눈으로 직접 확인해 보겠습니다. )
## Let's compare the elapsed time between 2 methods
## (list comprehension vs. vectorized operations)
## (1) List Comprehension
new_arr = [(x if c else y) for (x, y, c) in zip(xarr, yarr, cond)]
## (2) Vectorized Operations in NumPy
new_arr = np.where(cond, xarr, yarr)
(1) datetime.now() 메소드 이용해서 실행 시간 측정하기
datetime 모듈은 날짜, 시간, 시간대(time zone) 등을 다루는데 사용하는 모듈입니다 datetime.now() 메소드는 현재의 로컬 날짜와 시간을 반환합니다. 실행 시간을 측정할 코드 바로 앞에 start_time = datetime.now() 로 시작 날짜/시간을 측정해놓고, 실행할 코드가 끝난 다음 줄에 time_elapsed = datetime.now() - start_time 으로 '끝난 날짜/시간'에서 '시작 날짜/시간'을 빼주면 '코드 실행 시간'을 계산할 수 있습니다.
아래 결과를 비교해보면 알 수 있는 것처럼, for loop 순환문을 사용하는 List Comprehension 방법보다 NumPy의 Vectorized Operation이 약 38배 빠른 것으로 나오네요.
## (1) -- measuring the elapsed time using datetime
## (a) List Comprehension
from datetime import datetime
start_time = datetime.now()
list_comp_for_loop = [(x if c else y) for (x, y, c) in zip(xarr, yarr, cond)]
time_elapsed = datetime.now() - start_time
print('Time elapsed (hh:mm:ss.ms) {}'.format(time_elapsed))
# Time elapsed (hh:mm:ss.ms) 0:00:17.753036
np.array(list_comp_for_loop)[:10]
# array([0., 1., 2., 0., 0., 5., 6., 7., 8., 9.])
## (b) Vectorized Operations in NumPy
start_time = datetime.now()
np_where_vectorization = np.where(cond, xarr, yarr)
time_elapsed = datetime.now() - start_time
print('Time elapsed (hh:mm:ss.ms) {}'.format(time_elapsed))
# Time elapsed (hh:mm:ss.ms) 0:00:00.462215
np_where_vectorization[:10]
# array([0., 1., 2., 0., 0., 5., 6., 7., 8., 9.])
(2) %timeit 로 실행 시간 측정하기
다음으로 Python timeit 모듈을 사용해서 짧은 코드의 실행 시간을 측정해보겠습니다. timeit 모듈은 터미널의 command line 과 Python IDE 에서 호출 가능한 형태의 코드 둘 다 사용이 가능합니다.
아래에는 Jupyter Notebook에서 %timeit [small code snippets] 로 코드 수행 시간을 측정해본 예인데요, 여러번 수행을 해서 평균 수행 시간과 표준편차를 보여주는 특징이 있습니다.
## (2) measuring the elapsed time using timeit
## (a) List Comprehension
import timeit
%timeit list_comp_for_loop = [(x if c else y) for (x, y, c) in zip(xarr, yarr, cond)]
# 17.1 s ± 238 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
## (b) Vectorized Operations in NumPy
%timeit np_where_vectorization = np.where(cond, xarr, yarr)
# 468 ms ± 8.75 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
[Reference]
* Python datetime: https://docs.python.org/3/library/datetime.html
* Python timeit: "measuring the execution time of small code snippets"
: https://docs.python.org/3/library/timeit.html
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요!