[R] 칼럼을 역순으로 재정렬 하는 방법 (how to reverse the sequence of columns in R)
R 분석과 프로그래밍/R 데이터 전처리 2022. 12. 11. 22:12이번 포스팅에서는 R에서 칼럼의 순서를 역순으로 재정렬하는 3가지 방법을 소개하겠습니다.
(1) 위치 인덱싱 (position indexing)
(2) 수작업으로 칼럼 이름 인덱싱 (column name indexing manually)
(3) rev() 함수를 써서 역순 재정렬하여 칼럼 이름 인덱싱 (column name indexing using rev() function)
먼저 예제로 사용할 X1~X10의 10개의 칼럼으로 이루어진 간단한 DataFrame을 만들어보겠습니다.
## sample DataFrame with 10 columns
df <- data.frame(matrix(1:30, nrow=3))
print(df)
# X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
# 1 1 4 7 10 13 16 19 22 25 28
# 2 2 5 8 11 14 17 20 23 26 29
# 3 3 6 9 12 15 18 21 24 27 30
이제 X1~X5 까지는 순서를 역순으로 재정열하고, X6~X10은 원래의 순서를 그대로 유지하게끔 재정렬 해보겠습니다.
(before: X1, X2, X3, X4, X5, X6, X7, X8, X9, X10
after : X5, X4, X3, X2, X1, X6, X7, X8, X9, X10)
(1) 위치 인덱싱 (position indexing)
## X~X5를 역순으로 바꾸고, X6~X10은 그대로 두기
## (방법1) 위치(position) indexing
df2 <- df[c(5:1, # reverse
6:10)]
print(df2)
# X5 X4 X3 X2 X1 X6 X7 X8 X9 X10
# 1 13 10 7 4 1 16 19 22 25 28
# 2 14 11 8 5 2 17 20 23 26 29
# 3 15 12 9 6 3 18 21 24 27 30
(2) 수작업으로 칼럼 이름 인덱싱 (column name indexing manually)
## (방법2) 칼럼 이름으로 indexing
df3 <- df[c(paste0(rep("X", 5), 5:1), # reverse, manually
paste0(rep("X", 5), 6:10))]
print(df3)
# X5 X4 X3 X2 X1 X6 X7 X8 X9 X10
# 1 13 10 7 4 1 16 19 22 25 28
# 2 14 11 8 5 2 17 20 23 26 29
# 3 15 12 9 6 3 18 21 24 27 30
(3) rev() 함수를 써서 역순 재정렬하여 칼럼 이름 인덱싱 (column name indexing using rev() function)
## (방법3) 칼럼 이름으로 indexing, vec() 함수로 칼럼 이름 역순으로 재정렬
## column names
col_vec <- names(df)
print(col_vec)
# [1] "X1" "X2" "X3" "X4" "X5" "X6" "X7" "X8" "X9" "X10"
## reverse column names
rev(col_vec)
# [1] "X10" "X9" "X8" "X7" "X6" "X5" "X4" "X3" "X2" "X1"
df4 <- df[c(rev(col_vec[1:5]), # reverse, using rev() function
col_vec[6:10])]
print(df4)
# X5 X4 X3 X2 X1 X6 X7 X8 X9 X10
# 1 13 10 7 4 1 16 19 22 25 28
# 2 14 11 8 5 2 17 20 23 26 29
# 3 15 12 9 6 3 18 21 24 27 30
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요.
'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글
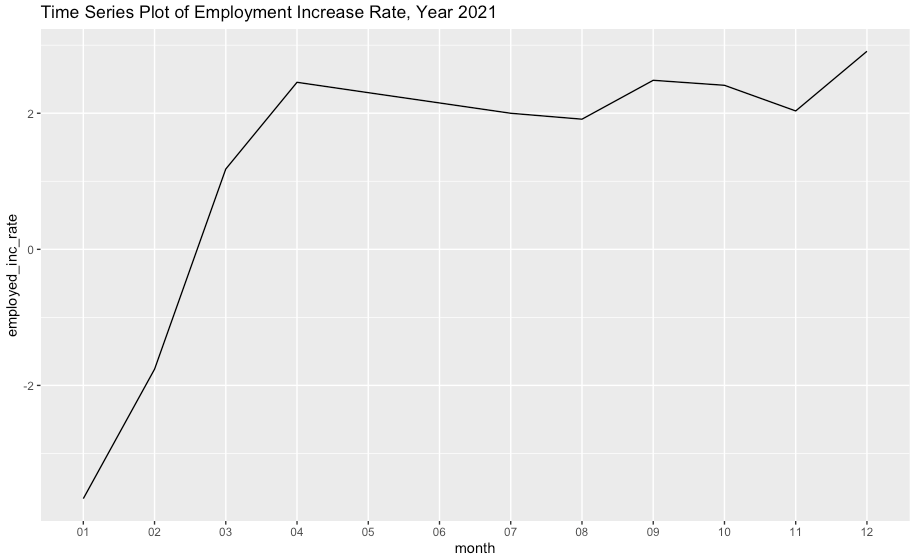
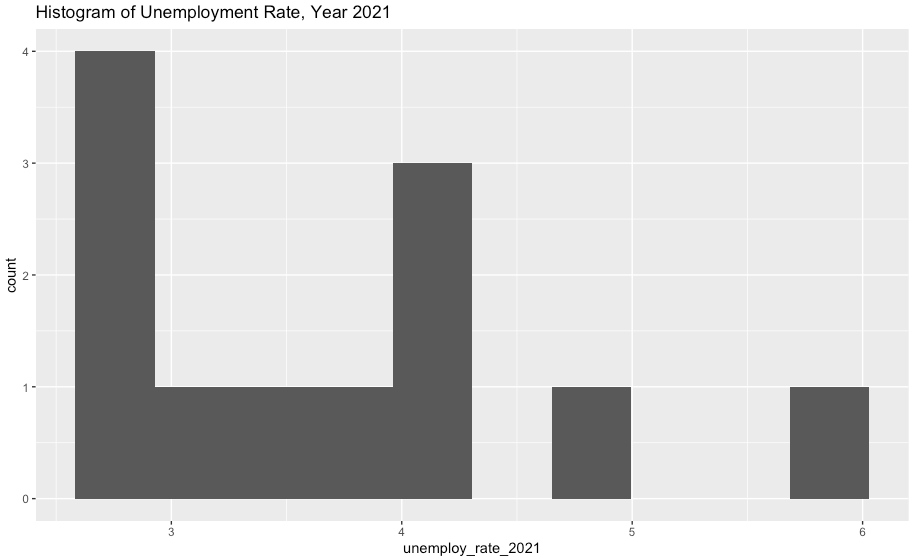
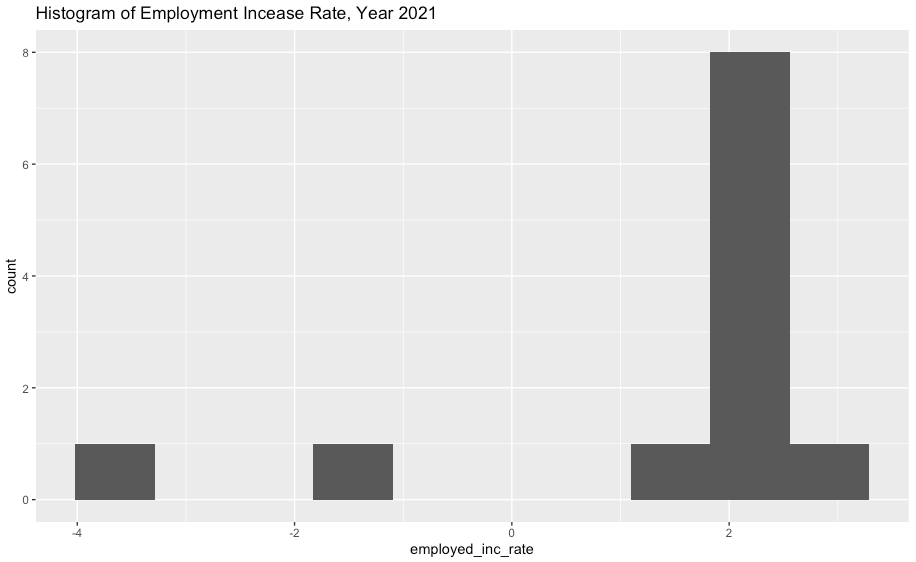
| [R] 실업률과 취업자수 데이터 전처리 및 시각화 (2) | 2022.10.10 |
|---|---|
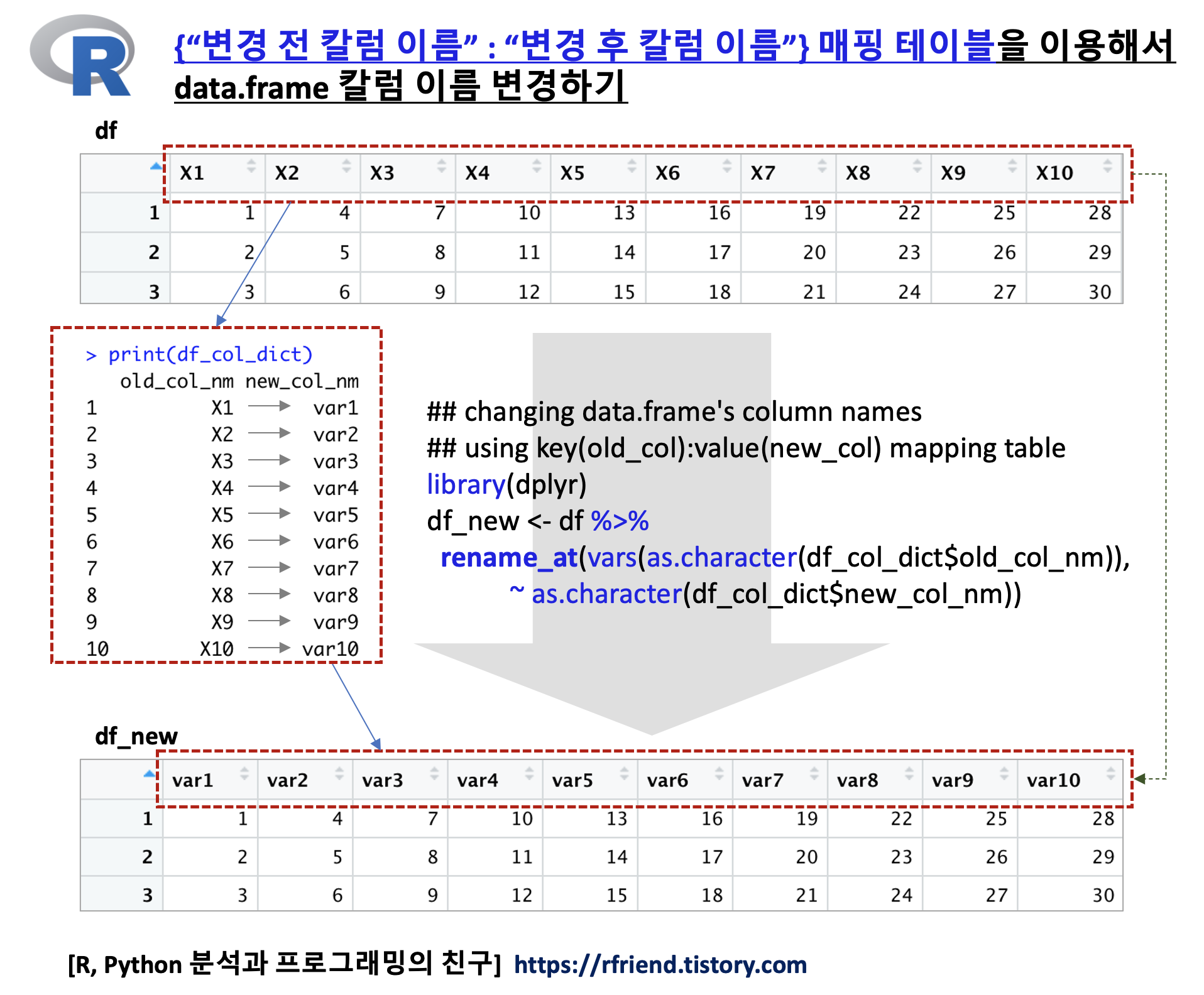
| [R] data.frame의 여러개 칼럼 이름을 old_col:new_col 의 매핑 테이블을 사용해서 변경하기 (13) | 2022.01.09 |
| [R data.table] 문자열 dcast 집계 함수 (1) 개수 (2) 콤마로 구분해서 붙여쓰기 (3) 첫번째 문자열만 가져오기 (0) | 2021.10.24 |
| [R] 시계열 데이터의 이동 평균, 누적 평균 구하기 (Average of time series using Rolling windows vs. Expanding windows) (4) | 2021.10.13 |
| [R data.table] 자동 인덱싱(Auto indexing)을 통한 빠른 탐색과 Subsetting (0) | 2021.02.11 |