이번 포스팅에서는 벡터(vector)의 정의와 연산에 대해서 알아보겠습니다.
벡터는 행렬과 함께 선형대수에서 많이 사용하는 개념이어서 꼭 이해하고 넘어가야 합니다. 벡터 개념과 연산은 중학교 수준의 수학 실력만 있으면 어렵지 않게 이해할 수 있으니 겁먹지 마시기 바랍니다. ^^
벡터(vector)는 여러 학문 분야에서 조금씩 다른 뜻으로 사용이 되고 있어서 혼선이 있을 수도 있는데요, 수학(mathemetics)과 컴퓨터 과학(computer science)에서 정의하는 벡터의 정의에 대해서만 살펴보겠습니다.
[ 수학과 컴퓨터과학에서 벡터의 정의 ]
|
[mathematics]
vector : a quantity possessing both magnitude and direction, represented by an arrow the direction of which indicates the direction of the quantity and the length of which is proportional to the magnitude.
* compare scalar : a quantity, such as time or temperature, that has magnitude but not direction
[computers]
vector : an array of data ordered such that individual items can be located with a single index or subscript
* source : http://dictionary.reference.com/browse/vector
|
수학(mathematics)이나 물리학에서는 벡터(vector)는 힘(magnitude)과 방향(direction)을 함께 가지고 있는 양을 말합니다. 화살표로 표현을 하는데요, 화살표의 길이는 힘(lennth of arrow = magnitude)을, 화살표의 방향은 힘의 방향(direction of arrow = direction)을 나타냅니다. 날아가는 야구공, 미사일 등이 벡터(vector)로 힘과 방향을 표현할 수 있겠습니다.
벡터는 보통 a, b, c, ... 처럼 소문자로 굵게(bold) 표기하거나 또는 a = [aj]와 같이 대괄호 안에 성분 표시를 합니다. (참고로, 행렬은 보통 A, B, C, ... 처럼 대문자로 굵게 표기하죠)
반면에, 스칼라(scalar)는 시간이나 온도와 같이 힘만 있고 방향은 없는(only magnitude, but not direction) 양을 말합니다. 특별한 가정이 없는 한 실수(real number)로 나타냅니다.
컴퓨터(computers) 분야에서는 벡터를 개별적인 요소들이 한개의 index나 subscript에 나열할 수 있는 데이터의 배열이라고 정의합니다.
[ 벡터의 정의 ]

벡터의 힘의 크기(magnitude of vector)는 아래 처럼 벡터의 양쪽 바깥쪽에 수직 막대를 한개 또는 두개(절대값 absolute와 혼돈하지 말라고)를 그어주는 것으로 표기합니다.
벡터의 힘의 크기는 유클리디안거리(Euclidean distance) 개념으로 계산합니다.
[ 벡터의 힘의 크기 (magnitude of vector) ]

벡터의 힘의 크기가 1인 벡터를 단위벡터(unit vector)라고 합니다.
[ 단위벡터 (unit vector) ]

열벡터(column vector)는 n by 1 행렬을 말하며, 행벡터(row vector)는 1 by n 행렬을 말합니다.
[ n by 1 열벡터(column vector)와 1 by n 행벡터(row vector) ]

특히 n by 1 벡터 전체로 이루어지는 집합을 R에 이중선을 추가해서

이라고 표기합니다.
선형대수 공부할 때, 최적화 선형계획법 공부할 때 자주 접하게 되는 표기법 중에 하나입니다.
[ 2 by 1, 3 by 1, n by 1 column vector ]

벡터(vector)는 아래와 같이 다양하게 해석할 수 있습니다. 벡터 [3, 5]를 예로 들어서 설명해보겠습니다.
- 해석 1 : 점 (4, 5)
- 해석 2 : 원점(0, 0)과 점(4, 5)를 이은 화살표
- 해석 3 : 원점(0, 0)에서 점(4, 5)까지 가는 화살표들의 합
- 해석 4 : 오른쪽으로 4, 위쪽으로 5만큼 이동하는 모든 화살표 (무수히 많음)
[ 벡터의 다양한 해석 ]

특히, 4번째 해석은 좀 의아할 수도 있는데요, 두 벡터의 크기와 방향이 같을 때, 즉 평행이동했을 때 서로 겹쳐지는 벡터를 '벡터의 상등(equality)'이라고 말하며, 무수히 많이 존재합니다.
행렬은 행벡터 또는 열벡터로 구성되며, 벡터는 행 또는 열이 1개인 행렬이라고 할 수 있습니다. 벡터의 계산은 행렬의 계산과 같습니다.
아래에 벡터끼리의 합, 차, 스칼라곱, 곱에 대한 예를 들어보겠습니다.
(1) 벡터의 합 (adding vectors)
벡터 a는 ax와 ay로 분할할 수 있습니다. 두 벡터 a와 b의 합은 a + b = (ax + bx, ay + by) 로 계산하게 됩니다.
아래에 벡터 a=[4, 5], 벡터 b=[3, 1]의 합 a+b를 예로 들어보았습니다.

R을 활용한 벡터의 합은 행렬의 합과 동일합니다. 벡터 a, b를 객체로 할당하고 + 하면 됩니다.
|
> ## adding vectors
>
> a <- c(4, 5)
> b <- c(3, 1)
>
> a
[1] 4 5
> b
[1] 3 1
>
> a+b
[1] 7 6 |
두개의 n by 1 열벡터 a와 b의 합은 아래와 같이 나타낼 수 있습니다.
[ 열 벡터a와 열 벡터b의 합(adding vectors) ]

(2) 벡터의 차 (substracting vectors)
벡터의 차는 같은 위치의 벡터의 성분끼리 빼주면 됩니다. 화살표로는 기존의 벡터의 방향을 반대로 돌려주는 것이 (-)해주는 의미가 되겠습니다. 벡터의 차는 두 점 사이의 거리를 계산할 때 요긴하게 사용할 수 있습니다.
두 벡터 a=[4, 5], b=[3, 1]의 차이를 아래에 예로 들어보았습니다.
[ 벡터의 차 (substracting vectors) ]

R로 벡터의 차를 구하는 것도 역시 행렬과 동일하게 두 벡터 객체에 (-) 해주면 됩니다.
|
> ## substracting vectors
> a <- c(4, 5)
> b <- c(3, 1)
>
> a
[1] 4 5
> b
[1] 3 1
>
> a-b
[1] 1 4
|
두 개의 m by 1 열벡터 a와 b의 차는 아래와 같이 나나탤 수 있습니다.
[ 열열터 a와 b의 차 (substracting vectors) ]

(3) 스칼라배 (multiplying a vector by a scalar)
위에서 스칼라를 힘만 있고 방향은 없는 양(a quantity that has only magnitude, but not direction)이라고 정의했었는데요, 벡터에 스칼라를 곱하는 것을 스칼라배라고 하고, 곱한 스칼라이 양만큼 벡터의 크기가 바뀌기 때문에 "벡터를 scaling한다"("scaling a vector")고도 합니다.
아래에 벡터 a=[2, 4]에 scalar 2, scalar 1/2 을 곱해보는 예제를 살펴보겠습니다. 방향은 똑같고 스칼라배한만큼 힘의 크기가 달라졌음을 알 수 있습니다.

아래에 위의 예제를 R로 스칼라배 연산해보았습니다.
|
> ## multiplying a vector by a scalar
> a <- c(2, 4)
>
> scala_1 <- c(2)
> scala_2 <- c(1/2)
>
> a*scala_1
[1] 4 8
>
> a*scala_2
[1] 1 2
|
n by 1 벡터a에 c스칼라배 하는 것은 아래와 같이 나타낼 수 있습니다.
[ 스칼라배 (multiplying a vector by a scala) ]

스칼라배는 행렬의 곱이 가지고 있는 특성을 고스란히 가지고 있습니다.
[ 행렬의 스칼라배 성질 (principle of multiplying a vector by a scala) ]

벡터의 곱(multiplying a vector by a vector, dot product, cross product)은 다음 포스팅에서 소개하도록 하겠습니다.
많은 도움이 되었기를 바랍니다.
행렬, 벡터 관련 포스팅은 아래 링크를 걸어놓았습니다.
☞ 행렬 기본 이해
☞ 특수한 형태의 행렬
☞ 가우스 소거법을 활용한 역행렬 계산
☞ 행렬의 기본 연산 (+, -, *, /, ^, %*%, colMeans(), rowMeans(), colSums(), rowSums())
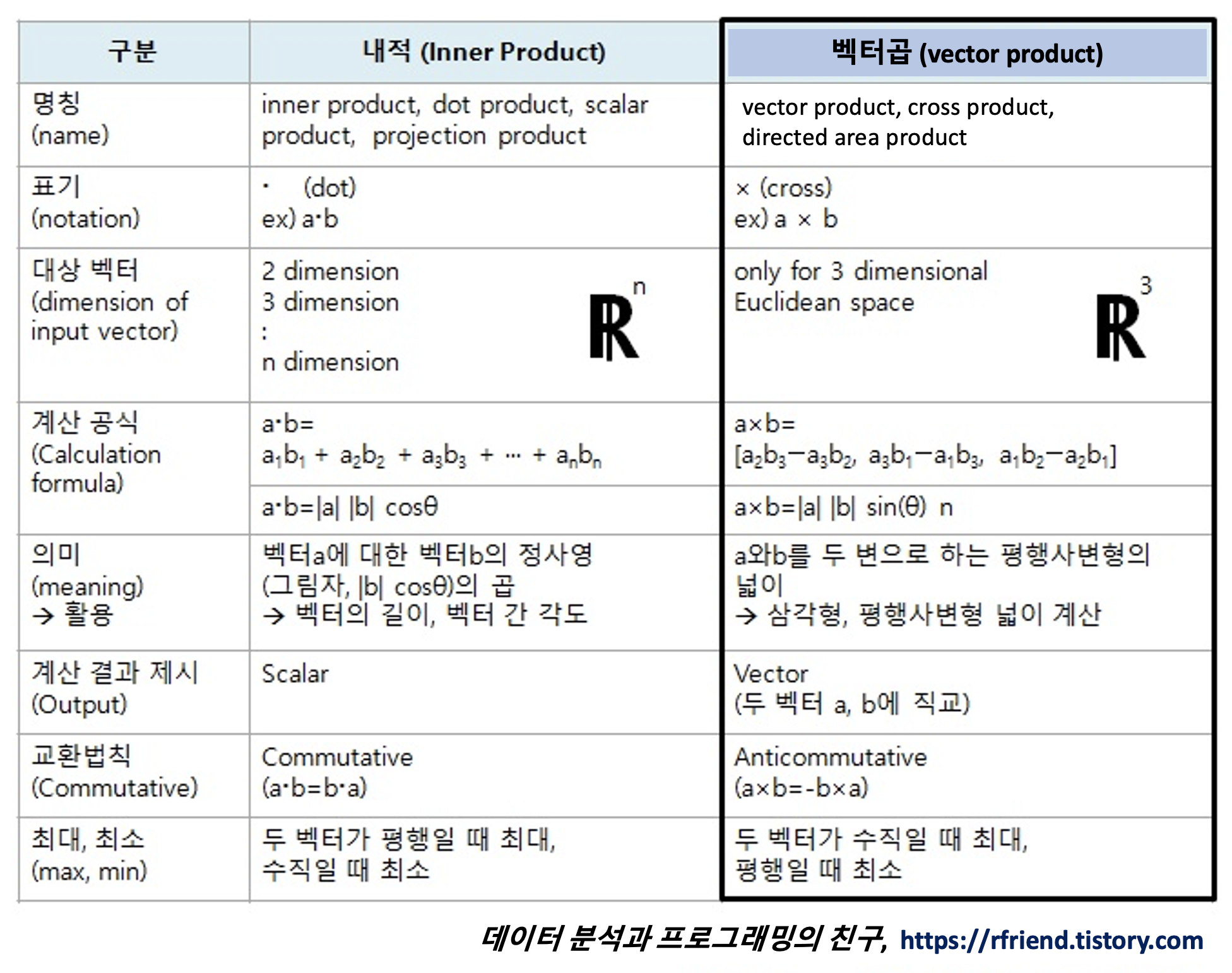
☞ 벡터의 곱 (1) 내적 (inner product, dot product, scalar product, projection product)
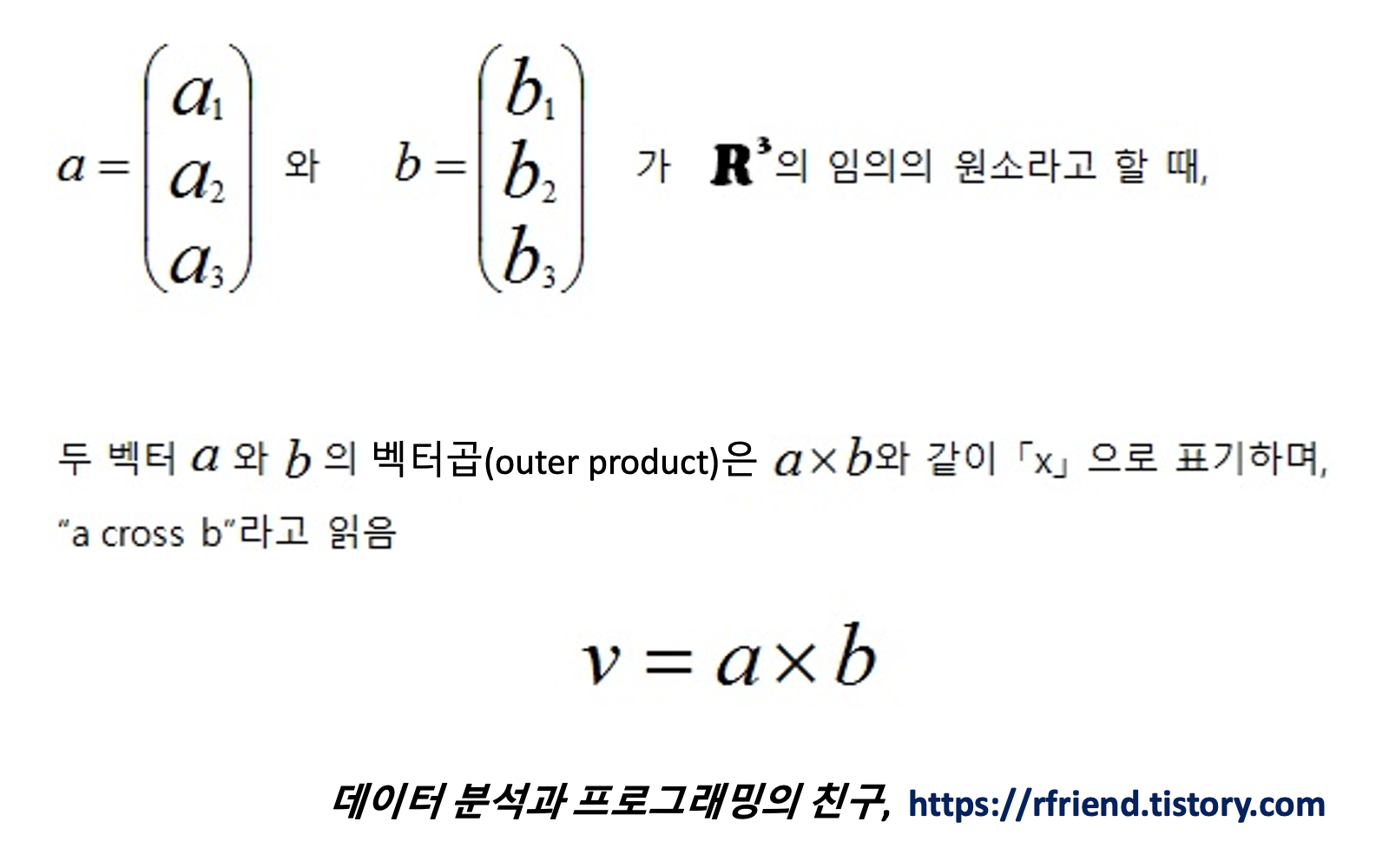
☞ 벡터의 곱 (2) 외적 (outer product, cross product, vector product, tensor product)
이번 포스팅이 도움이 되었다면 아래의 공감 ♡ 꾸욱~ 눌러주세요. ^^