기울기 소실 문제(Vanishing Gradient Problem)란 무엇이고, 어떻게 완화할 수 있나?
Deep Learning (TF, Keras, PyTorch)/PyTorch basics 2023. 12. 13. 15:48이번 포스팅에서는 심층 신경망을 훈련하는 과정에서 발생하는 문제 중의 하나로 기울기 소실 문제 (Vanishing Gradient Problem) 에 대해서 다루어보겠습니다.
1. 기울기 소실 문제은 무엇인가?
(What is the Vanishing Gradient Problem?)
2. 기울기 소실 문제에 기여하는 주요 요인은 무엇인가?
(What are the key factors contributing to the vanishing gradient problem?)
3. 기울기 소실 문제를 완화할 수 있는 방법은 무엇인가?
(How to mitigate the vanishing gradient problem?)
1. 기울기 소실 문제은 무엇인가?
(What is the Vanishing Gradient Problem?)
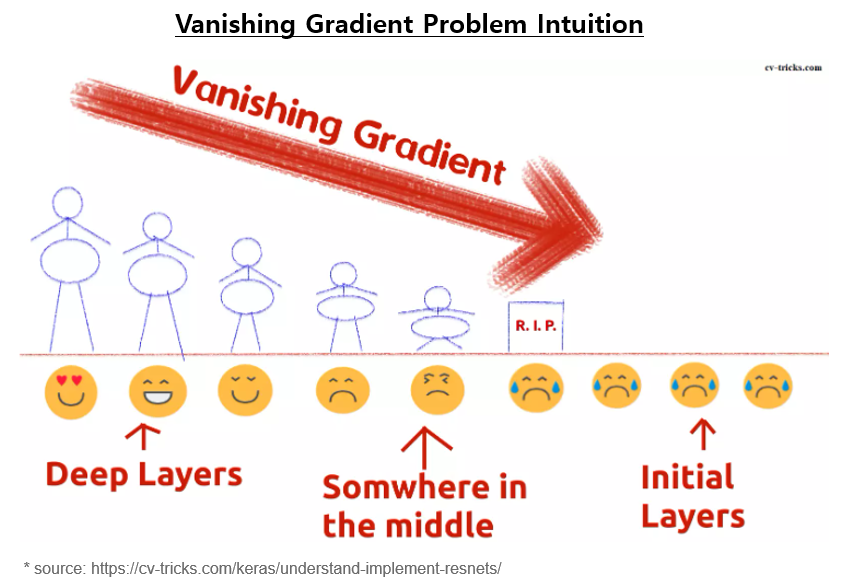
기울기 소실 문제 (Vanishing Gradient Problem)은 특히 많은 층을 갖는 심층 신경망을 훈련하는 과정에서 발생하는 어려움입니다. 이는 훈련 과정 중에 네트워크를 통해 그래디언트가 역전파될 때 손실 함수에 대한 가중치와 편향의 그래디언트가 극도로 작아지는 문제를 나타냅니다. 그래디언트가 거의 0에 가까워지면 네트워크의 가중치가 효과적으로 업데이트되지 않을 수 있으며, 네트워크는 데이터에서 학습하는 데 어려움을 겪을 수 있습니다.
기울기 소실 문제 (Vanishing Gradient Problem)는 특히 순환 신경망 (RNN)이나 심층 피드포워드 신경망(Deep Feedforward Neural Network)과 같은 심층 아키텍처에서 두드러지며, 오류의 역전파는 각 층의 업데이트에서 많은 작은 그래디언트 값을 서로 곱함으로써 기울기 소실로 이어집니다. 이 작은 값들의 곱셈은 기울기 소실을 초래하여 전체적으로 소실된 그래디언트를 초래할 수 있습니다.
2. 기울기 소실 문제에 기여하는 주요 요인은 무엇인가?
(What are the key factors contributing to the vanishing gradient problem?)
(1) 활성화 함수 (Activation Functions)
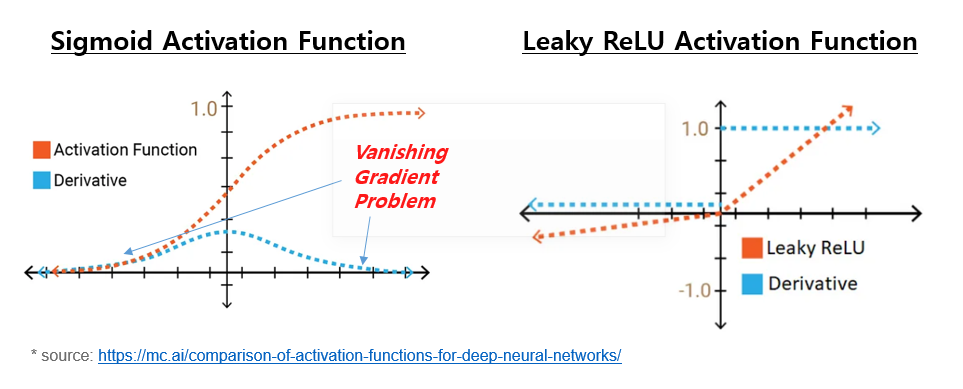
일부 활성화 함수, 특히 시그모이드(Sigmoid) 또는 쌍곡선 탄젠트 (Hyperbolic tangent, tanh)와 같은 함수는 극단적인 입력 값에 대해 포화됩니다. 이러한 영역에서 그래디언트는 거의 0에 가까워져 네트워크가 유용한 그래디언트를 역방향으로 전파하는 것을 어렵게 만듭니다.
(2) 네트워크의 깊이 (Depth of the network)
신경망의 층 수가 증가함에 따라 소실 그래디언트를 만날 확률도 높아집니다. 그래디언트는 여러 층을 통해 역전파되어야 하며, 각 층은 그래디언트가 소실되기에 추가 기회를 제공합니다.
(3) 가중치 초기화 (Weight Initialization)
가중치 초기화를 잘못 선택하면 기울기 소실 문제가 악화될 수 있습니다. 가중치가 너무 작게 초기화되면 그래디언트가 층을 통과할 때 소실될 수 있습니다.
(4) 네트워크 아키텍처 (Network Architecture)
순환 신경망(RNN)이나 심층 신경망(Deep Neural Network)과 같이 특정 아키텍처 선택은 소실 그래디언트 문제를 강화할 수 있습니다.
3. 기울기 소실 문제를 완화할 수 있는 방법은 무엇인가?
(How to mitigate the vanishing gradient problem?)
(1) 활성화 함수 (Activation Function)
해당 입력 범위에서 포화 문제가 없는 활성화 함수를 사용하십시오. ReLU(Rectified Linear Unit)는 양수 입력 값에 대해 포화되지 않는 일반적으로 사용되는 활성화 함수입니다.
## Use Activation Functions That Do Not Saturate like ReLU, using PyTorch
# define a simple nueral network
class SimpleNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNN, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU() # Rectified Linear Unit Activation Function
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
return x
# Usage
model = SimpleNN()
(2) 배치 정규화 (Batch Normalization)
배치 정규화는 미니 배치의 평균을 빼고 표준 편차로 나누어 신경망 층의 입력을 정규화함으로써 소실 그래디언트 문제를 완화합니다. 다음은 배치 정규화가 소실 그래디언트 문제에 대처하는 데 도움이 되는 방법입니다.
- 정규화 (Normailzation): 배치 정규화는 미니 배치의 평균을 빼고 표준 편차로 나누어 층의 입력을 정규화합니다. 이로써 다음 층의 입력이 대략적으로 0 주변에 집중되고 표준 편차가 약 1이 되도록 보장됩니다.
- 활성화 함수 안정화(Stablizing Activation Functions): 시그모이드 또는 tanh와 같은 특정 활성화 함수는 입력이 너무 크거나 작을 때 포화됩니다. 배치 정규화는 입력을 정규화하여 입력이 안정된 범위에 유지되도록 돕습니다. 이로써 기울기 소실 문제의 일반적인 원인인 활성화 함수의 포화를 방지합니다.
- 내부 공변량 변화 감소 (Reducing Internal Covariate Shift): 배치 정규화는 훈련 중에 층의 입력 분포가 변경되는 내부 공변량 변화를 감소시킵니다. 입력을 정규화함으로써 배치 정규화는 입력 분포의 변화를 완화시켜 최적화 과정을 안정화시킵니다.
- 더 높은 학습률 허용 (Allowing Higher Learning Rates): 배치 정규화는 더 높은 학습률을 사용할 수 있게 합니다. 높은 학습률은 최적화 알고리즘이 빠르게 수렴하는 데 도움을 줄 수 있습니다. 배치 정규화 없이 높은 학습률을 사용하면 소실 그래디언트 문제로 인해 발산하거나 수렴이 느려질 수 있습니다.
- 가중치 초기화에 대한 독립성 (Independence from Weight Initialization): 배치 정규화는 가중치 초기화 선택에 대한 민감성을 줄입니다. 배치 정규화가 없으면 나쁜 가중치 초기화가 소실 그래디언트 문제를 악화시킬 수 있습니다. 배치 정규화는 학습 동적을 초기화로부터 분리하여 훈련을 더 견고하게 만듭니다.
이러한 문제들을 해결함으로써 배치 정규화는 특히 기울기 소실 문제가 두드러지는 깊은 아키텍처에서 효과적으로 학습하도록 도와줍니다.
## Batch Normalization using PyTorch
## Batch Normalization
import torch
import torch.nn as nn
class SimpleNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(YourModel, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.bn1 = nn.BatchNorm1d(hidden_size) # Batch Normalization
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.bn1(x) # Batch Normalization
x = self.relu(x)
x= self.fc2(x)
return x
# Usage
model = SimpleNN()
(3) 가중치 초기화 (Weight Initialization)
신호 전파를 촉진하는 방식으로 초기 가중치를 설정하는 적절한 가중치 초기화 기술을 사용하십시오. 예를 들면, Xavier/ Glorot 초기화가 있습니다.
## Xavier Initialization using PyTorch
import torch.nn.init as init
class YourModel(nn.Module):
def __init__(self):
super(YourModel, self).__init__()
self.fc1 = nn.Linear(in_features, out_features)
# Initialize weights using Xavier/Glorot initialization
init.xavier_uniform_(self.fc1.weight)
# Usage
model = YourModel()
(4) 스킵 연결 (Skip Connections)
심층 신경망에서 스킵 연결(Skip Connections) 또는 잔차 연결(Residual Connections)은 정보를 층 간에 직접 흐르게 해 소실 그래디언트를 완화하는 데 도움이 됩니다. ResNet과 같은 아키텍처에서 사용됩니다.
기울기 소실 문제를 해결하는 것은 심층 신경망을 효과적으로 훈련시키기 위해 중요하며, 아키텍처 선택 및 다양한 기술의 조합이 그 영향을 완화하는 데 도움이 될 수 있습니다.
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요. :-)




