딥러닝에서 오차역전파법 (Backpropagation, Backward Propagation of Errors) 이란?
Deep Learning (TF, Keras, PyTorch)/PyTorch basics 2023. 12. 12. 23:57인공신경망이 인풋 데이터와 정답(label) 데이터를 가지고 학습을 한다고 했을 때, 신경망의 내부에서 무슨 일이 일어나고 있는지, 기계가 데이터를 가지고 학습을 하는 원리가 무엇인지 궁금하실거예요. 이번 포스팅은 바로 이 마법에 대한 소개 글입니다.
"오차역전파(Backpropagation)"은 "오차를 역방향으로 전파하는 방법 (backward propagation of errors)" 의 줄임말로서, 인공 신경망을 훈련시키기 위한 지도 학습 알고리즘으로 자주 사용됩니다. 이는 신경망이 오류에서 학습하고 시간이 지남에 따라 성능을 향상시킬 수 있도록 하는 훈련 과정에서 중요한 구성 요소입니다.
다음은 오차역전파 알고리즘이 학습하는 단계입니다.
1. 초기화 (Initialization)
2. 순방향 전파 (Forward Pass)
3. 오류 계산 (Calculate Error)
4. 역방향 전파 (Backward Pass, Backpropagation)
5. 경사 하강법 (Gradient Descent)
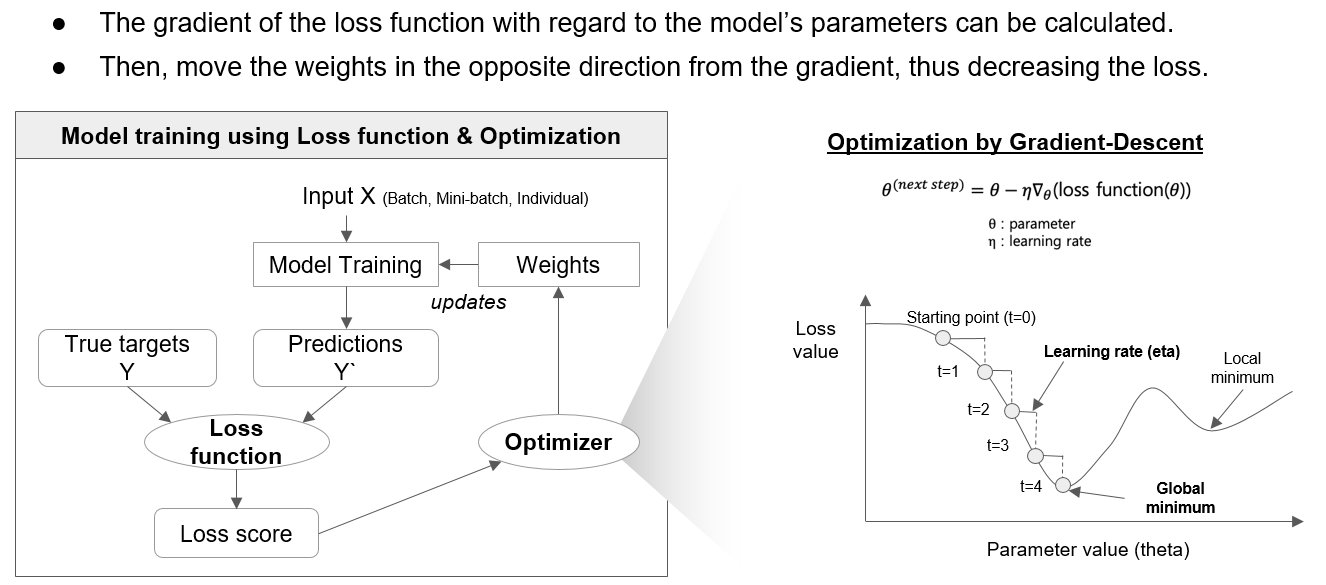
[ 손실함수와 경사하강법에 의한 최적화를 통한 모델 훈련 ]
1. 초기화 (Initialization)
신경망에서 초기화(Initialization)는 훈련이 시작되기 전에 네트워크의 가중치(Weights)와 편향(Biases)을 설정하는 과정을 나타냅니다. 올바른 초기화는 신경망의 성공적인 훈련에 중요하며 모델의 수렴 및 성능에 큰 영향을 미칠 수 있습니다.
신경망을 만들 때 그 가중치 및 편향을 일정한 값으로 초기화합니다. 이러한 초기 값의 선택은 네트워크가 얼마나 빨리 학습하며 올바른 해법으로 수렴하는지에 영향을 줄 수 있습니다. 부적절한 초기화는 수렴이 느리게 되거나 그라디언트가 소멸하거나 폭발하는 등의 문제를 초래할 수 있습니다.
가중치 초기화에는 여러 기법이 있으며, 일반적으로 사용되는 몇 가지 방법에는 다음이 포함됩니다.
(1) 랜덤 초기화(Random Initialization): 가중치에 무작위 값 할당하기. 이는 흔한 접근법으로, 가우시안(정규) 분포 또는 균일 분포를 사용하여 무작위 값 생성하는 방법을 사용할 수 있습니다.
(2) 자비에/글로럿 초기화(Xavier/Glorot Initialization): 이 방법은 시그모이드 및 쌍곡선 탄젠트(tanh) 활성화 함수와 잘 작동하도록 설계되었습니다. 가중치는 평균이 0이고 분산이 (1/ 입력 뉴런 수) 인 가우시안 분포에서 값들을 추출하여 초기화됩니다.
(3) He 초기화(He Initialization): "ReLU 초기화"로도 알려져 있으며, ReLU 활성화 함수를 사용하는 네트워크에 적합합니다. 가중치는 평균이 0이고 분산이 (2/ 입력 뉴런 수) 인 가우시안 분포에서 값들을 추출하여 초기화됩니다.
적절한 초기화 방법을 선택하는 것은 사용된 활성화 함수에 따라 다르며, 신경망을 효과적으로 훈련시키기 위한 중요한 측면입니다. 적절한 초기화 기술을 사용하면 훈련 중 발생하는 일반적인 문제를 완화하고 더 안정적이고 빠른 수렴에 기여할 수 있습니다.
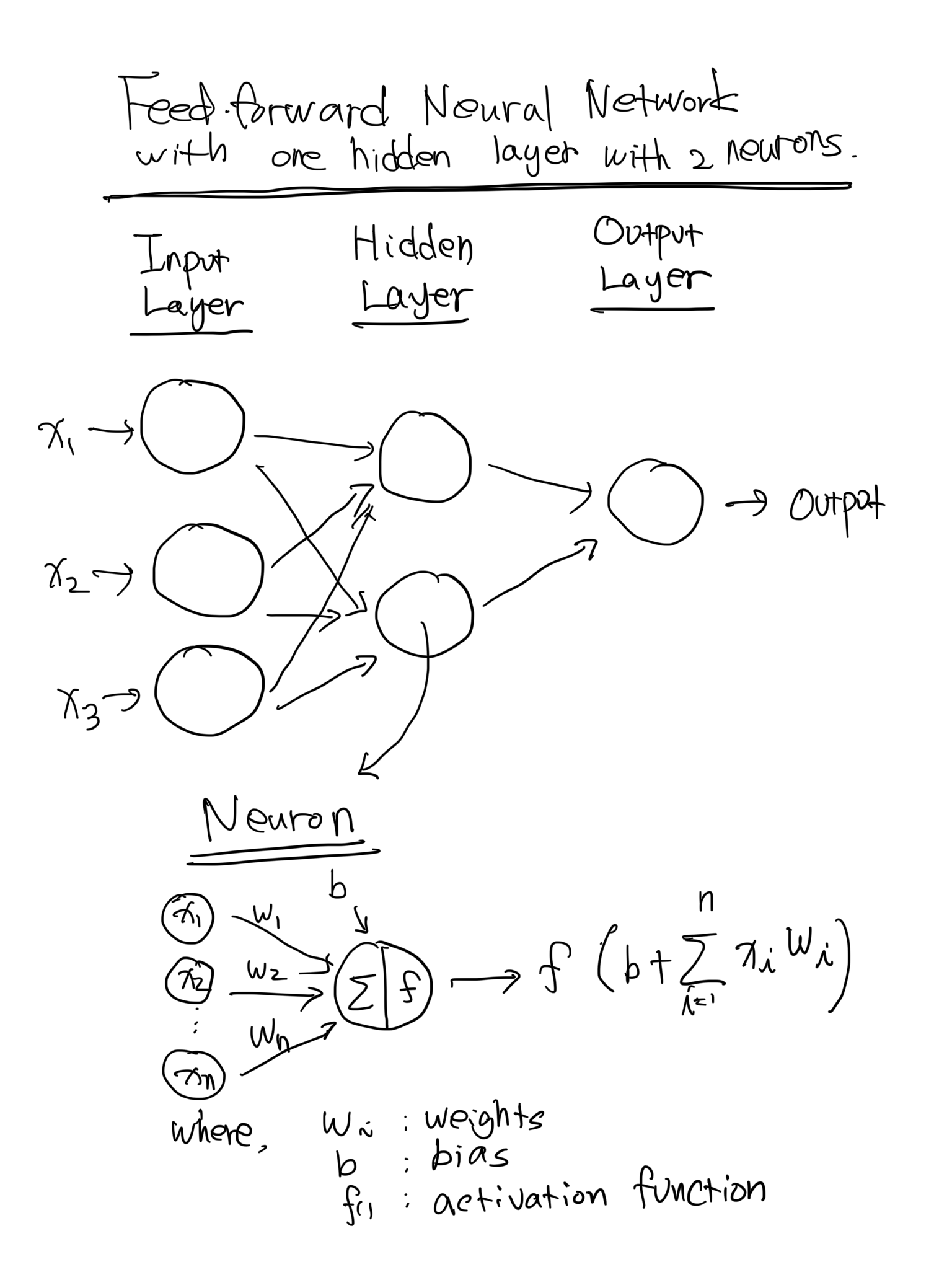
2. 순방향 전파 (Forward Pass)
신경망에서의 순전파(forward pass)는 입력 데이터를 네트워크를 통과시켜 출력을 생성하는 과정을 나타냅니다. 순전파 중에는 입력 데이터가 신경망의 각 층을 통과하고, 각각의 층에서 변환을 거쳐 최종 출력을 생성합니다.
순전파의 단계를 설명하면 다음과 같습니다.
(1) 입력 층(Input Layer): 데이터 입력, 즉 데이터 세트의 특징들이 신경망의 입력 층에 공급됩니다.
(2) 가중치와 편향(Weights and Biases): 인접한 층 사이의 각 뉴런 간에는 가중치가 할당됩니다. 이러한 가중치는 연결의 강도를 나타냅니다. 또한 각 뉴런은 편향(bias) 항을 갖습니다. 입력 데이터는 가중치로 곱해지고 편향이 결과에 더해집니다.
(3) 활성화 함수(Activation Function): 입력과 편향의 가중 합은 활성화 함수를 통과합니다. 이는 신경망에 비선형성을 도입하여 데이터의 복잡한 관계를 학습할 수 있도록 합니다. 일반적인 활성화 함수로는 ReLU(렐루), 시그모이드, tanh 등이 있습니다.
(4) 출력(Output): 활성화 함수의 결과는 해당 층의 출력이 되고, 이는 네트워크의 다음 층에 대한 입력으로 전달됩니다.
(5) 과정 반복(Repeating the process): 2~4단계는 각각의 이전 층에 대해 반복되어 네트워크의 모든 층을 통과합니다. 최종 출력은 일반적으로 출력 층(Output Layer)에서 생성됩니다.
순전파는 예측 단계에서 정보가 네트워크를 통과하는 방식입니다. 네트워크는 학습된 가중치와 편향을 사용하여 입력 데이터를 의미 있는 예측으로 변환합니다. 순전파의 출력은 실제 대상 값과 비교되며, 이 오차는 역전파(backpropagation) 단계에서 가중치와 편향을 업데이트하는 데 사용되어 네트워크가 시간이 지남에 따라 학습하고 성능을 향상시킬 수 있도록 합니다.
3. 오류 계산 (Calculate Error)
신경망의 출력은 손실 함수(loss function)를 사용하여 실제 목표 값(실제 값)과 비교됩니다. 이는 예측 값과 실제 출력 간의 차이를 측정합니다. 이 손실 함수를 최소화하는 것이 목표로, 이는 네트워크의 예측이 가능한 한 실제 값에 가까워지도록 합니다.
다양한 유형의 손실 함수가 있으며, 사용할 적절한 손실 함수의 선택은 해결하려는 문제의 성격에 따라 다릅니다. 일반적인 손실 함수에는 다음이 포함됩니다.
(1) 평균 제곱 오차 (Mean Squared Error, MSE): 회귀 문제(Regression problem)에 적합하며, 예측된 값과 실제 값 간의 평균 제곱 차이를 계산합니다.
(2) 이진 교차 엔트로피 손실 (Binary Cross-Entropy Loss): 이진 분류 문제(Binary classification problem)에 사용되며, 예측된 확률 분포와 실제 분포 간의 불일치를 측정합니다.
(3) 다중 클래스 교차 엔트로피 손실 (Categorical Cross-Entropy Loss): 다중 클래스 분류 문제(Multi-class classification problem)에 적합하며, 각 클래스에 대한 예측된 확률 분포와 실제 분포 간의 불일치를 측정합니다.
(4) 힌지 손실 (Hinge Loss): 서포트 벡터 머신(Support Vector Machine, SVM)에서 흔히 사용되며, 일부 분류 작업에서도 사용됩니다.
손실 함수의 선택은 학습 과정에 영향을 미치며, 주어진 작업의 특수한 요구사항과 특성과 일치하는 손실 함수를 선택하는 것이 중요합니다. 최적화 알고리즘은 훈련 중에 계산된 손실을 기반으로 모델 매개변수를 조정하여 시간이 지남에 따라 모델의 성능을 향상시키려고 노력합니다.
4. 역방향 전파 (Backward Pass, Backpropagation)
역전파(Backward Pass, Backpropagation)는 신경망을 훈련시키는 중요한 단계입니다. 입력 데이터가 네트워크를 통과하여 예측을 생성하는 순전파 이후에는 역전파를 사용하여 계산된 손실에 기초해 모델의 매개변수(가중치와 편향)를 업데이트합니다. 이 과정의 목표는 예측된 출력과 실제 목표 값 사이의 차이를 최소화하는 것입니다.
아래는 역전파 오류 전파 과정의 주요 단계입니다.
(1) 출력에 대한 손실의 그래디언트 계산 (Compute Gradient of the Loss with Respect to the Output) : 손실 함수의 그래디언트를 모델의 출력에 대해 계산합니다. 이 단계에서는 출력이 조정될 경우 손실이 얼마나 변하는지를 결정합니다.
(2) 네트워크를 통한 그래디언트 역전파 (Compute Gradient of the Loss with Respect to the Output) : 그래디언트를 네트워크의 층을 통해 역방향으로 전파합니다. 이는 미적분의 연쇄 법칙을 적용하여 각 층의 가중치와 편향에 대한 손실의 그래디언트를 계산하는 것을 포함합니다.
(3) 가중치와 편향 업데이트 (Update Weights and Biases) : 계산된 그래디언트를 사용하여 네트워크의 가중치와 편향을 업데이트합니다. 최적화 알고리즘인 확률적 경사 하강법(SGD) 또는 그 변형 중 하나는 손실을 줄이는 방향으로 매개변수를 조정합니다.
(4) 다중 반복에 대해 반복 (Repeat for Multiple Iterations (Epochs)) : 단계 1-3은 여러 번의 반복 또는 에폭에 대해 반복되며 각 반복에서는 훈련 샘플의 배치가 처리됩니다. 이 반복적인 프로세스를 통해 네트워크는 매개변수를 조정하여 시간이 지남에 따라 성능을 향상시킬 수 있습니다.
역전파의 수학적 세부 사항은 편미분(partial derivatives)과 연쇄 법칙(the chain rule)을 포함합니다. 구체적으로 그래디언트는 오류를 층을 통해 역방향으로 전파함으로써 계산되며, 가중치와 편향은 그래디언트의 반대 방향으로 업데이트됩니다.
[ The Chain Rule]

[ example: Partial Derivative of w1 with respect to E1 ]
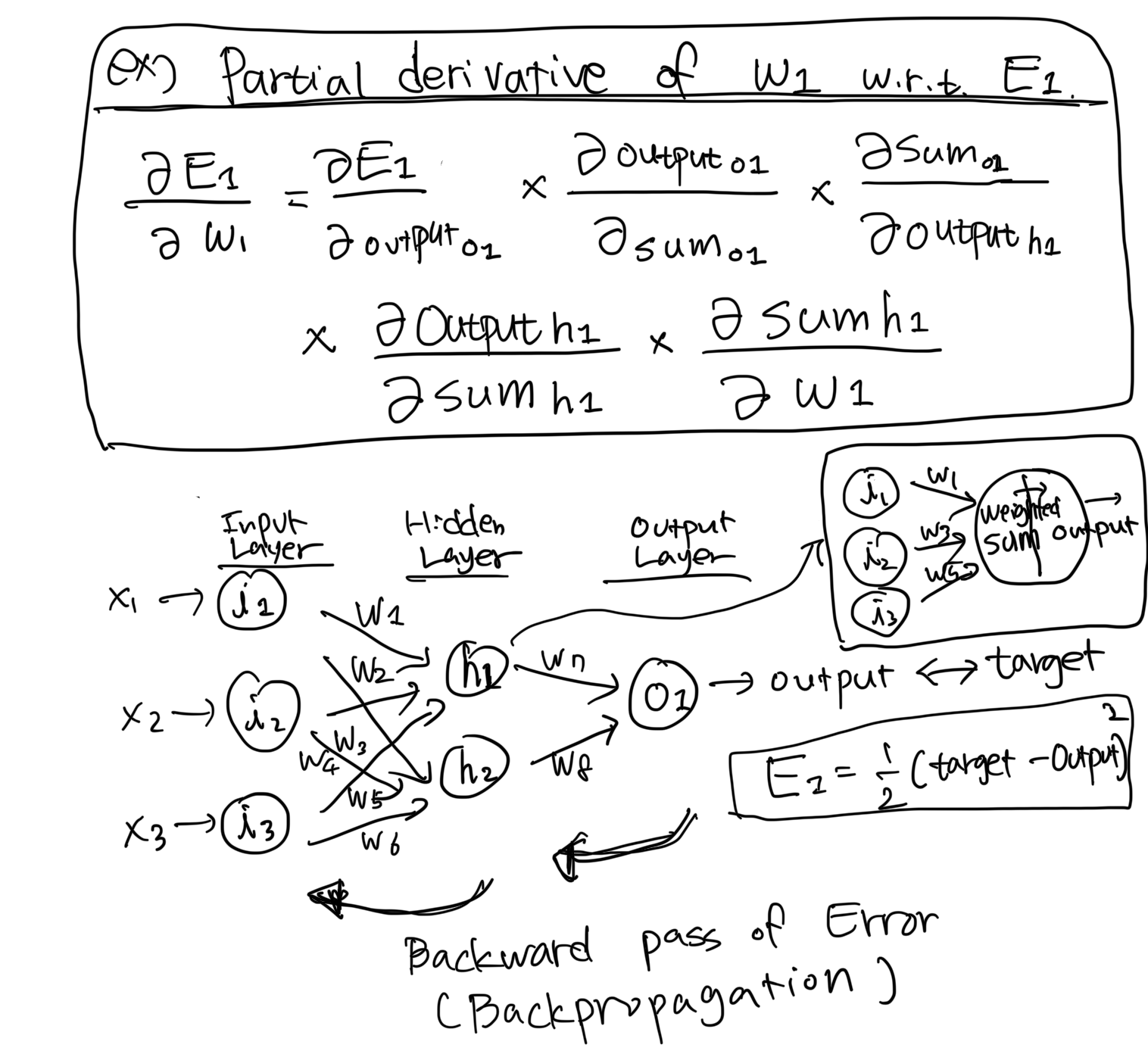
역전파는 신경망을 훈련시키는 데 기본 개념으로, 네트워크가 실수에서 학습하고 매개변수를 계속해서 조정할 수 있게 합니다. 이 반복적인 과정을 통해 모델은 새로운, 보지 않은 데이터에 대한 예측을 더 잘 수행하게 됩니다.
5. 경사 하강법 (Gradient Descent)
계산된 도함수는 손실을 줄이는 방향으로 가중치와 편향을 업데이트하는 데 사용됩니다.
이를 위해 일반적으로 경사 하강 최적화 알고리즘(Optimization by Gradient-Descent)이 사용되며, 학습률에 의해 스케일링된 기울기의 일부를 빼서 가중치와 편향을 조절합니다.

- Eta (η)는 학습율(the learning rate)로서, 학습율은 기계 학습 및 신경망 훈련에서 사용되는 하이퍼파라미터 중 하나로, 각 훈련 단계에서 모델의 가중치를 조정하는 정도를 나타냅니다. 즉, 학습율은 가중치 업데이트의 크기(step size)를 결정하는 매개변수입니다.
높은 학습율은 각 단계에서 더 큰 가중치 업데이트를 의미하며, 이는 모델이 빠르게 학습할 수 있게 할 수 있습니다. 그러나 너무 높은 학습율은 수렴을 방해하고 발산(explosion)할 수 있기 때문에 조심스럽게 선택되어야 합니다.
낮은 학습율은 더 안정적인 학습을 제공하지만, 수렴하는 데 더 많은 시간이 걸릴 수 있습니다. 또한, 지역 최솟값(local optima)에서 빠져나오기 어려울 수 있습니다.
적절한 학습율을 선택하는 것은 모델의 성능과 수렴 속도에 큰 영향을 미칩니다. 학습율은 하이퍼파라미터 튜닝 과정에서 조정되며, 실험을 통해 최적의 값을 찾는 것이 일반적입니다. 일반적으로는 0.1, 0.01, 0.001과 같은 값을 시도하며 Cross-validation을 통해 모델의 성능을 평가하여 최적의 학습율을 결정합니다.
다음은 오차역전파법을 설명하기 위해 가상으로 만든, 각 레이어 별로 input size = 3, hidden size 1 = 3, hidden size 2 = 3, output size = 1 의 모델 아키텍처를 가지는 아주 간단한 PyTorch 예시가 되겠습니다. MSE 를 손실함수로 하고, Adam optimizer를 사용하였습니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
# Define the neural network architecture with hyperparameters
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size_1, hidden_size_2, output_size):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size_1)
self.bn1 = nn.BatchNorm1d(hidden_size_1)
self.fc2 = nn.Linear(hidden_size_1, hidden_size_2)
self.bn2 = nn.BatchNorm1d(hidden_size_2)
self.fc3 = nn.Linear(hidden_size_2, output_size)
def forward(self, x):
x = F.relu(self.bn1(self.fc1(x)))
x = F.relu(self.bn2(self.fc2(x)))
x = self.fc3(x)
return x
# Set Hyperparameters
input_size = 3
hidden_size_1 = 6
hidden_size_2 = 3
output_size = 1
epochs = 100
learning_rate = 0.001
# Initiate the network
model = SimpleNet(input_size, hidden_size_1, hidden_size_2, output_size)
print(model)
# SimpleNet(
# (fc1): Linear(in_features=3, out_features=6, bias=True)
# (bn1): BatchNorm1d(6, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
# (fc2): Linear(in_features=6, out_features=3, bias=True)
# (bn2): BatchNorm1d(3, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
# (fc3): Linear(in_features=3, out_features=1, bias=True)
# )
GPU 를 사용할 수 있으면 Device를 "cuda"로, CPU를 사용할 수 있으면 Device를 "cpu"로 설정해줍니다. 아래 예에서는 Tesla V100 16G GPU를 사용하므로 "cuda"로 Device를 설정해주었습니다.
# Check for CUDA availability
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
# cuda
#### when you run at Jupyter Notebook, add '!' at the beginning.
! nvidia-smi -L
# GPU 0: Tesla V100-SXM2-16GB (UUID: GPU-d445249d-b63e-5e62-abd1-7646bb409870)
Loss 함수는 MSE (Mean Squared Error) 로 설정하였고, Optimizer는 Adam 으로 설정해주었습니다.
모델 훈련에 사용할 데이터셋을 난수를 발생시켜서 생성하고, 위에서 지정한 Device 에 모델의 파라미터와 버퍼, 그리고 데이터를 이동시켰습니다 (modeo.to(device), torch.randn((100, input_size)).to(device)).
# Move the model's parameters and buffers to the specified device.
model.to(device)
# Set Loss and Optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# Generate dummy input and target data, move the data to the specified device
inputs = torch.randn((100, input_size)).to(device)
targets = torch.randn((100, output_size)).to(device)
Epochs = 100 만큼 for loop 순환문을 사용해서 반복하면서 모델을 훈련 시킵니다. Forward pass, Calculate loss, Backward pass, Update weights (Optimize) 의 과정을 반복합니다.
# Training phase
model.train() # training mode
for epoch in range(epochs):
# Forward pass
output = model(inputs)
loss = criterion(output, targets) # calculate loss
# Backward pass and optimize
optimizer.zero_grad() # clear previous gradients
loss.backward() # compute gradients, backward pass
optimizer.step() # update weights
# Print training statistics
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# Epoch [10/100], Loss: 0.9778
# Epoch [20/100], Loss: 0.9476
# Epoch [30/100], Loss: 0.9217
# Epoch [40/100], Loss: 0.9000
# Epoch [50/100], Loss: 0.8826
# Epoch [60/100], Loss: 0.8674
# Epoch [70/100], Loss: 0.8534
# Epoch [80/100], Loss: 0.8423
# Epoch [90/100], Loss: 0.8329
# Epoch [100/100], Loss: 0.8229
위에서 훈련한 모델에 가상으로 만든 1개의 샘플 데이터를 인풋으로 넣어서 예측을 해보겠습니다. 배치가 아니가 단 1개의 샘플 데이터만 사용하기 때문에 model.eval() 을 해주었습니다. (만약 model.eval() 을 추가해주지 않으면, ValueError: Expected more than 1 value per channel when training, got input size torch.Size([1, 2]) 가 발생합니다.)
# Example of using the trained model
test_input = torch.randn((1, input_size)).to(device)
model.eval() # evaluation mode
with torch.no_grad():
predicted_output = model(test_input)
print("Test Input:", test_input)
print("Predicted Output:", predicted_output.item())
# Test Input: tensor([[ 0.3862, 0.1250, -0.3322]], device='cuda:0')
# Predicted Output: -0.00717635452747345
위에서 학습이 완료된 인공신경망 모델의 레이어 이름과 파라미터별 가중치, 편향에 접근해서 확인해보도록 하겠습니다.
## (1) Access to the names and parameters in the trained model
for name, param in model.named_parameters():
print(name)
print(param)
print("-----" * 15)
# fc1.weight
# Parameter containing:
# tensor([[-0.0542, -0.5121, 0.3793],
# [-0.5354, -0.1862, 0.4207],
# [ 0.3339, -0.0813, -0.2598],
# [ 0.5527, -0.3505, -0.4357],
# [-0.0351, -0.0992, 0.1252],
# [-0.2110, 0.0713, -0.2545]], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# fc1.bias
# Parameter containing:
# tensor([ 0.5726, 0.1125, 0.4138, -0.1896, 0.1353, -0.0372], device='cuda:0',
# requires_grad=True)
# ---------------------------------------------------------------------------
# bn1.weight
# Parameter containing:
# tensor([0.9044, 0.9735, 1.0557, 0.9440, 1.0983, 1.0414], device='cuda:0',
# requires_grad=True)
# ---------------------------------------------------------------------------
# bn1.bias
# Parameter containing:
# tensor([-0.1062, 0.0177, 0.0283, -0.0527, 0.0059, -0.0117], device='cuda:0',
# requires_grad=True)
# ---------------------------------------------------------------------------
# fc2.weight
# Parameter containing:
# tensor([[-0.3057, 0.0730, 0.2711, 0.0770, 0.0497, 0.4484],
# [-0.3078, 0.0153, 0.1769, 0.2855, -0.4853, 0.2110],
# [-0.3342, -0.2749, 0.3440, -0.2844, 0.0763, -0.1959]],
# device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# fc2.bias
# Parameter containing:
# tensor([-0.0536, -0.3275, 0.0371], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# bn2.weight
# Parameter containing:
# tensor([1.0843, 0.9524, 0.9426], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# bn2.bias
# Parameter containing:
# tensor([-0.0564, 0.0576, -0.0848], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# fc3.weight
# Parameter containing:
# tensor([[-0.4607, 0.4394, -0.1971]], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
# fc3.bias
# Parameter containing:
# tensor([-0.0125], device='cuda:0', requires_grad=True)
# ---------------------------------------------------------------------------
## (2) Access to the weights and biases in the trained model
print("[ Model FC1 Weights ]")
print(model.fc1.weight.cpu().detach().numpy())
print("-----" * 10)
print("[ Model FC2 Weights ]")
print(model.fc2.weight.cpu().detach().numpy())
# [ Model FC1 Weights ]
# [[-0.05423066 -0.51214963 0.37927148]
# [-0.53538287 -0.18618222 0.42071185]
# [ 0.33391565 -0.08127454 -0.2597795 ]
# [ 0.55268896 -0.3505293 -0.4356556 ]
# [-0.03507916 -0.09922788 0.1251672 ]
# [-0.21096292 0.07126608 -0.25446963]]
# --------------------------------------------------
# [ Model FC2 Weights ]
# [[-0.30573702 0.07304495 0.27107015 0.07700069 0.04968859 0.44840544]
# [-0.3078182 0.01533379 0.17685111 0.28549835 -0.485255 0.21100621]
# [-0.33416617 -0.27492833 0.3440289 -0.28436708 0.07630474 -0.19592032]]
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요. :-)

'Deep Learning (TF, Keras, PyTorch) > PyTorch basics' 카테고리의 다른 글
| [PyTorch] 원소 간 곱 vs. 행렬곱 (element-wise product vs. matrix multiplication) (0) | 2023.12.16 |
|---|---|
| 기울기 소실 문제(Vanishing Gradient Problem)란 무엇이고, 어떻게 완화할 수 있나? (0) | 2023.12.13 |
| [PyTorch] torchvision.datasets 모듈에 내장되어 있는 데이터 가져와서 시각화하기 (0) | 2023.02.26 |
| [PyTorch] 텐서 나누기 (splitting a PyTorch tensor into multiple tensors) (0) | 2023.02.23 |
| [PyTorch] 텐서 합치기 (concat, stack) (0) | 2023.02.21 |



