[Python] 분류 모델 성능 평가 지표 (evaluation metrics for classification model)
Python 분석과 프로그래밍/Python 기계학습 2023. 1. 23. 20:35이번 포스팅에서는 분류 모델 (classification model) 의 성능을 비교 평가할 수 있는 지표(evaluation metrics)들에 대해서 소개하겠습니다.
(1) 혼돈 매트릭스 (Confusion Matrix)
(2) 혼돈 매트릭스 기반 분류 모델 성능 평가 지표
- 정확도 (Accuracy)
- 재현율 (Recall rate), 민감도 (Sensitivity)
- 특이도 (Specificity)
- 정밀도 (Precision)
- F-1 점수 (F-1 Score)
(3) 정밀도와 재현율의 상충 관계 (Precision/ Recall Trade-off)
(4) 분류 확률 기반 ROC Curve, AUC (Area Under the ROC Curve)
(5) Python 을 이용한 분류 모델 성능 평가 (다음번 포스팅)
(1) 혼돈 매트릭스 (Confusion Matrix)
먼저 범주의 정답(Y, Label)을 알고 있는 데이터의 실제 값 (Actual) 과 분류 모델을 통해 분류한 예측 값 (Predicted) 을 평가하여 아래와 같은 표의 형태로 객체의 수를 셉니다. Positive 는 '1'/ 'Success'/ 'Pass'/ 'Live' 등에 해당하며, Negative 는 '0'/ 'Fail'/ 'Non Pass'/ 'Dead' 등을 의미합니다.
TP (True Positive), FP (False Positive), FN (False Negative), TN (True Negative) 는 아래의 표를 보면 의미가 더 명확할거예요. (P와 N은 예측치를 의미하며, 이걸 실제 값과 비교했을 때 맞혔으면 True, 틀렸으면 False 로 표기한 것임)
책에 따라서 '실제 값 (Actual)'과 '예측 값 (Predicted)' 의 축이 다른 경우도 있으니 가로 축과 세로 축이 무엇을 의미하는지 꼭 확인이 필요합니다.

(2) 혼돈 매트릭스 기반 분류 모델 성능 평가 지표
모든 관측치의 개수를 N (= TP + TN + FP + FN) 이라고 하면,
- 정확도 (Accuracy) = (TP + TN) / N
- 재현율 (recall rate), 민감도 (Sensitivity) = TP / (TP + FN)
- 특이도 (Specificity) = TN / (FP + TN)
- 정밀도 (Precision) = TP / (TP + FP)
- F1 점수 (F1 Score) = 1 / (1/Precision + 1/Recall)
의 수식을 이용해서 구할 수 있습니다.
F-1 점수 (F-1 Score)는 정밀도와 재현율의 조화평균(harmonic mean, 역수의 산술평균의 역수)으로서, 정밀도와 재현율이 균형있게 둘 다 높을 때 F-1 점수도 높게 나타납니다. 정밀도와 재현율이 모두 중요한 경우에는 F-1 점수를 사용해서 모델을 평가하면 됩니다.

(3) 정밀도와 재현율의 상충 관계 (Precision/ Recall Trade-off)
정밀도(Precision)와 재현율(Recall rate)은 분류 예측을 위한 의사결정 기준점(decision threshold)을 얼마로 하느냐에 따라 달라집니다. (의사결정 기준점에 따라 혼돈 매트릭스의 4사분면의 각 숫자가 달라짐)
정밀도와 재현율은 상충 관계에 있어서, 마치 시소 게임처럼 정밀도가 높아지면 재현율이 낮아지고, 반대로 재현율이 높아지면 정밀도는 낮아집니다. 이 상충관계를 잘 이해해야 왜 이렇게 많은 분류 모델 성과평가 지표가 존재하고 필요한지 이해할 수 있습니다.
보통은 '양성(Positive, 1)' 으로 분류할 확률이 의사결정 기준점 '0.5' 보다 크면 '양성 (Positive, 1)' 로 분류하고, '0.5' 보다 같거나 작으면 '음성 (Negative, 0)' 으로 분류를 합니다. (아래 그림의 (2)번 케이스)
만약 '실제 양성' (Actual Positive) 을 더 많이 잡아내고 싶으면 (실제 음성을 양성으로 오분류할 비용을 감수하고서라도), 의사결정 기준점을 내려주면 됩니다. (아래 그림의 (1)번 케이스) 그러면 재현율(Recall rate)은 올라가고, 정밀도(Precision) 은 낮아집니다.
만약 '예측한 양성'이 실제로도 양성인 비율 (즉, 정밀도, Precision)을 높이고 싶으면 의사결정 기준점을 올려주면 됩니다. (아래 그림의 (3)번 케이스). 그러면 정밀도(Precision)은 올라가고, 재현율(Recall rate)은 내려가게 됩니다.
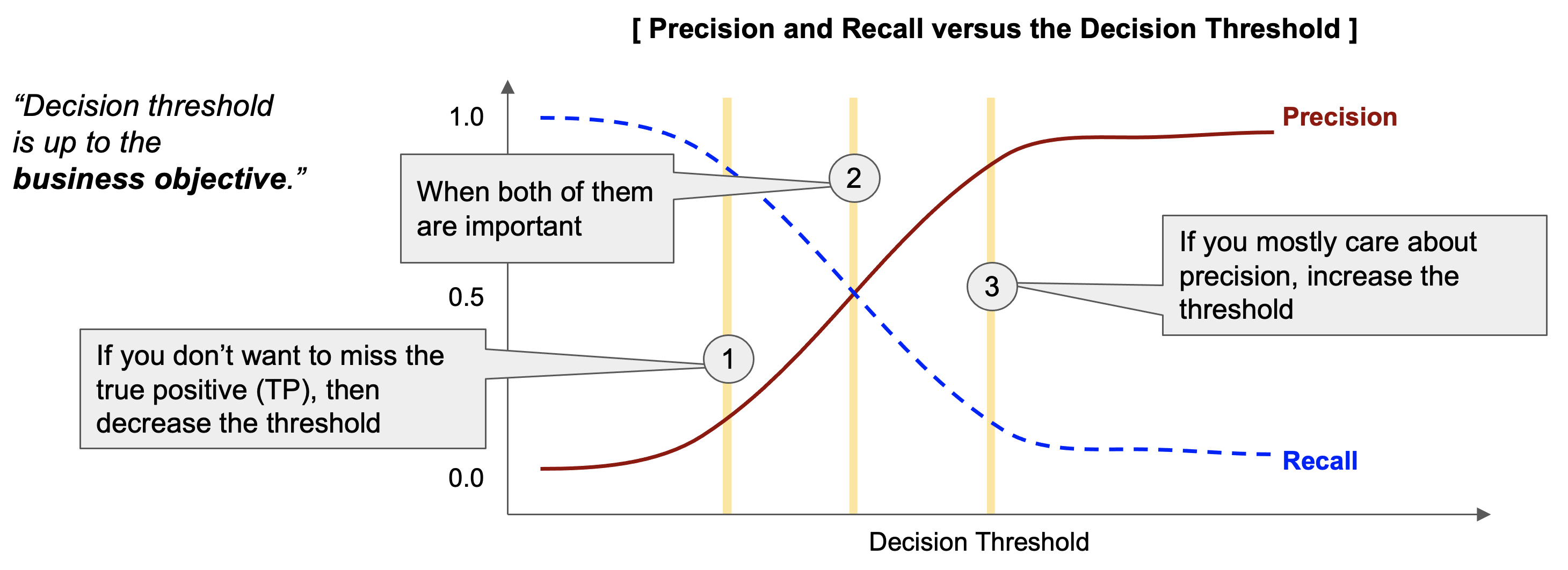
의사결정 기준점을 변경하고 싶다면 비즈니스 목적 상 재현율과 정밀도 중에서 무엇이 더 중요한 지표인지, 실제 양성을 놓쳤을 때의 비용과 예측한 양성이 실제로는 음성이었을 때의 비용 중에서 무엇이 더 끔찍한 것인지를 생각해보면 됩니다.
가령, 만약 코로나 진단 키트의 분류 모델이라면 '실제 양성 (즉, 코로나 감염)' 인 환자가 '음성'으로 오분류 되어 자가격리 대상에서 제외되고 지역사회에 코로나를 전파하는 비용이 '실제 음성 (즉, 코로나 미감염)' 인 사람을 '양성'으로 오분류했을 때보다 비용이 더 크다고 할 수 있으므로 (1) 번 케이스처럼 의사결정 기준점을 내려서 재현율(Recall rate)을 올리는게 유리합니다.
반면, 유튜브에서 영유아용 컨텐츠 적격 여부를 판단하는 분류모델을 만든다고 했을 때는, 일단 분류모델이 '영유아용 적격 판단 (Positive)' 을 내련 영상 컨텐츠는 성인물/폭력물/욕설 등의 영유아용 부적격 컨텐츠가 절대로 포함되어 있으면 안됩니다. 이럴경우 일부 실제 영유아용 적격 컨텐츠가 '부적격'으로 오분류되는 비용을 감수하고서라도 (3)번 케이스처럼 의사결정 기준점을 올려서 정밀도를 높게 해주는 것이 유리합니다.
그리고, 극도로 불균형한 데이터셋 (extremely imbalanced dataset) 의 경우 정확도(Accuracy) 지표는 모델을 평가하는 지표로 부적절합니다. 이때는 비즈니스 목적에 맞게 재현율과 정밀도 중에서 선택해서 사용하는 것이 필요합니다. (양성이 희소한 경우 모델이 모두 음성이라고 예측해도 정확도 지표는 매우 높게 나옴. 하지만 우리는 희소한 양성을 잘 찾아내는 모델을 원하지 모두가 다 음성이라고 예측하는 쓸모없는 모델을 원하지는 않음.)
(4) 분류 확률 기반 ROC Curve, AUC (Area Under the ROC Curve)
ROC 곡선(Receiver Operating Characteristic Curve)은 모든 분류 의사결정 기준값(decision threshold)에서 분류 모델의 성능을 보여주는 그래프입니다. X축은 False Positive Rate, Y축은 True Positive Rate 으로 하여 모든 의사결정 기준값 (Positive 일 확률) 별로 혼돈 매트릭스를 구하고, 여기에서 재현율과 특이도를 구해서 TPR과 FPR을 구하고, 이를 선으로 연결해주면 됩니다.
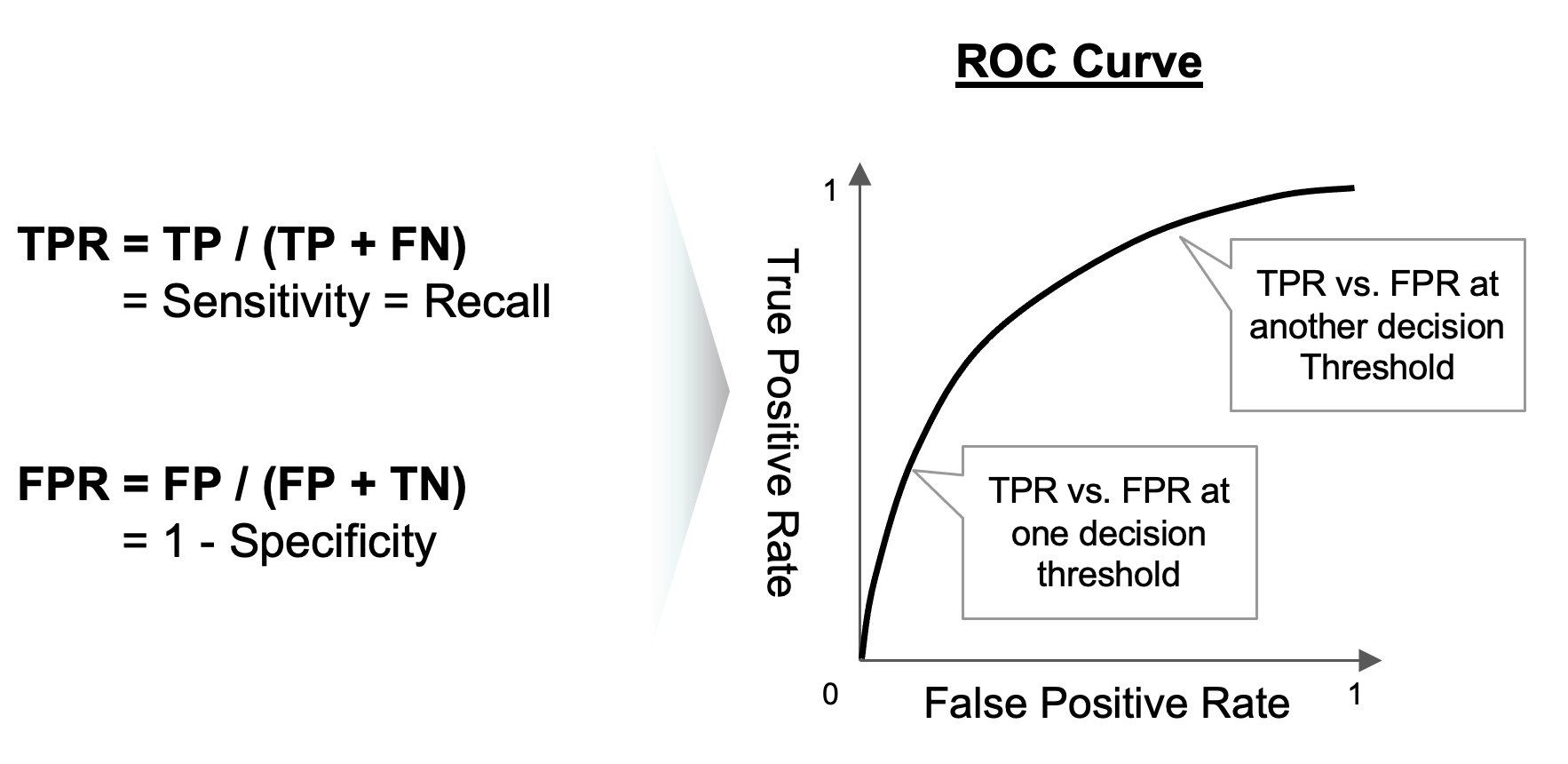
ROC 곡선은 45도 대각선이 무작위로 추측하여 분류했을 때를 의미하며, ROC 곡선이 좌측 상단으로 붙으면 붙을 수록 분류 모델의 성능이 더 좋다고 해석합니다. (False Positive Rate 보다 True Positive Rate이 상대적으로 더 높을 수록 더 좋은 분류 모델임)
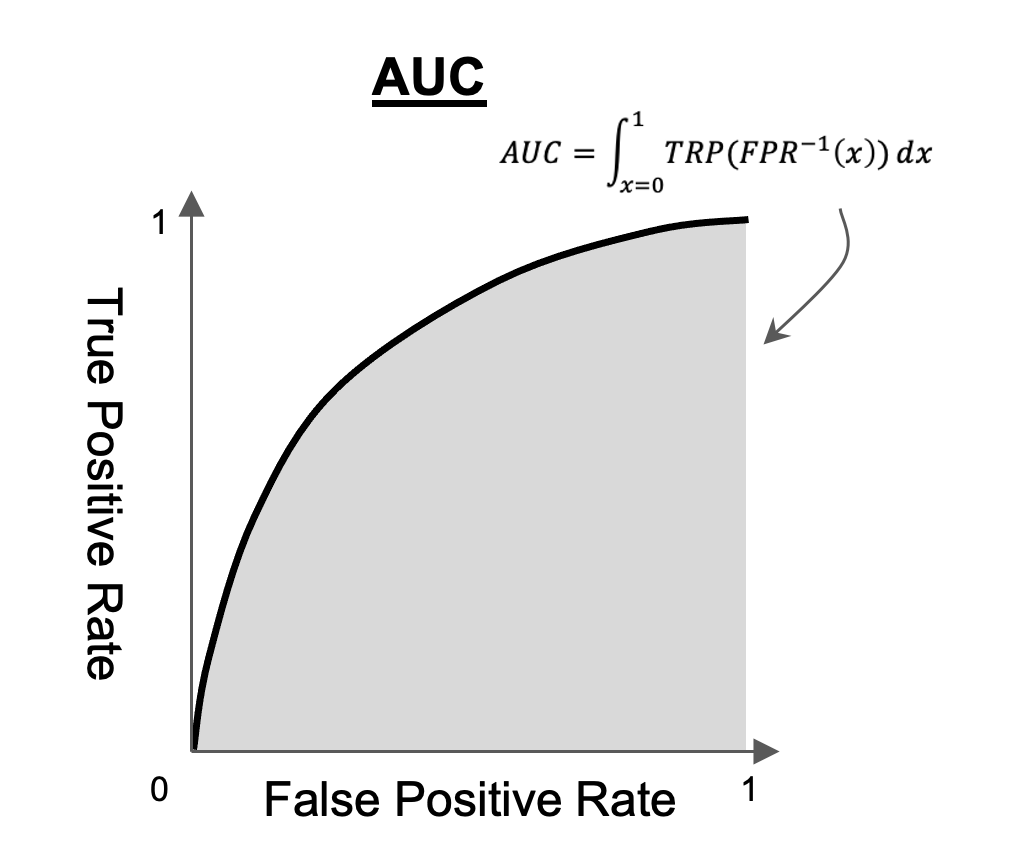
AUC (Area Under the ROC Curve) 점수는 위의 ROC 곡선의 아랫 부분을 적분하여 하나의 수치로 분류 모델의 성능을 표현한 것입니다. AUC 점수가 높으면 높을 수록 더 좋은 분류 모델입니다.
ROC 곡선과 AUC 모두 분류 모델이 '양성일 확률(probability)'을 반환할 때만 계산이 가능합니다.
(즉, 모델이 분류할 범주(category, class)로 예측값을 반환하면 ROC 곡선, AUC 계산 불가)
다음번 포스팅에서는 Python을 이용한 분류모델 성능 평가를 해보겠습니다.
(https://rfriend.tistory.com/772)
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)












