R, Python 분석과 프로그래밍의 친구 (by R Friend)

기계학습에서 Regularization 은 Penalization, Constraing method, Shrinkage methods 라고도 하는데요, "규제하다", "벌점을 주다", "제약을 가하다", "축소시키다" 등의 억압을 가하는 의미를 가지고 있습니다. 

보통 Regularization을 "정규화"라고 번역하는 경우가 많던데요, Normalization 도 "정규화"라고 번역을 하곤 해서 개념이 서로 혼동되기 쉬운 면이 있어서요, 이번 포스팅에서는 그냥 Regularization 을 그대로 사용하겠습니다. 굳이 번역하라면 "규제화"나 "벌점화", "(가중치) 축소화" 등으로 번역할 수 있을 거 같습니다.

이번 포스팅에서는 Regularization 이 무엇이며 왜 사용하는지에 대해 알아보겠습니다. 또한 Regularization 기술 및 그 사용 방법에 대해 소개할 것입니다. 

1. 기계 학습에서의 Regularization 은 무엇이고 왜 사용하는가? 
2. L1 Regularization (LASSO Regression)
3. L2 Regularization (Ridge Regression

4. Cross-validation을 이용한 Tuning Parameter Gamma 최적값 찾기
5. Python을 이용한 LASSO 예제 (w/ Hyper-parameter tuning)

1. 기계 학습에서의 Regularization 은 무엇이고 왜 사용하는가? 

Regularization 은 기계 학습에서 과적합(Overfitting)을 방지하기 위한 기술 중 하나로, 모델이 훈련 데이터에 지나치게 적합화되는 것을 막기 위해 사용됩니다. 과적합은 모델이 훈련 데이터의 잡음과 이상치까지 학습하여 새로운, 보지 못한 데이터에 대해 일반화하기 어렵게 만드는 현상입니다. 이러한 상황에서 모델은 훈련 데이터를 외우기보다는 기본적인 패턴을 학습하는 것이 중요합니다.

Regularization은 모델이 학습하는 파라미터의 계수 (coefficient estimages) 값에 제약을 가해서 '0'으로 가깝게 축소를 하거나 또는 정확하게 '0'으로 축소를 시킴으로써 계수 추정치의 분산을 줄이고(reducing the variance of the coefficients estimates) 모델의 복잡성을 제어하여 과적합을 피하게 해주는 효과가 있습니다. (대신에 Bias 는 늘어나는 비용을 지불하게 됩니다. 세상에 공짜가 없어요..>.<;). 

Regularization = Loss Function + Penalty

선형회귀모형을 예로 들어서 설명하면, Regularization 은 Penalty 항을 무엇을 사용하느냐에 따라

(1) L1 Regularization(LASSO), (2) L2 Regularization(Ridge), (3) ElasticNet 으로 구분할 수 있습니다. 

Tuning parameter Lambda(λ)는 모델에 적용되는 규제의 전반적인 강도를 제어하는 규제 강도 하이퍼파라미터입니다. 람다(λ) 값이 높아지면 더 강한 패널티가 적용되어 더 희소한 모델과 작은 계수 값이 생성됩니다. 

Elastic Net에 있는 Mix ratio 알파(α) (책에 따라 Alpha 대신 Gamma( γ )가 혼용되서 사용됨. Scikit-Learn 모듈에는 알파(α)  로 표기) 는 Elastic Net에서 L1 및 L2 패널티 항의 조합을 결정하는 하이퍼파라미터입니다. 

  - 알파(α)가 0이면 Elastic Net은 Ridge 회귀 (L2 Regularization)와 동일합니다.
  - 알파(α)가 1이면 Elastic Net은 Lasso 회귀 (L1 Regularization)와 동일합니다.
  - 알파(α)가 0과 1 사이의 값을 가지면 Elastic Net은 L1 및 L2 Regularization을 결합합니다.

요약하면, Elastic Net은 알파(α) 매개변수를 통해 L1 및 L2 Regularization을 조합하고, Regularization의 전반적인 강도는 람다(λ) 매개변수로 제어됩니다.

2. L1 Regularization (LASSO Regression*)

LASSO 회귀 또는 L1 Regularization은 모델의 목적 함수에 Penalty 항을 통합하는 선형 회귀 방법입니다. LASSO 회귀의 목표는 과적합을 방지하고 모델이 사용하는 특징의 일부만 사용하도록 유도하여 실질적으로 변수 선택(Feature Selection)을 수행하는 것입니다.

표준 선형 회귀 목적 함수는 예측 값과 실제 값 간의 제곱 차이의 합을 최소화하는 것입니다. 그러나 LASSO 회귀에서는 이 목적 함수에 회귀계수의 절대값의 합이 페널티 항으로 추가되어 수정된 목적 함수는 다음과 같습니다. 즉, 기존의 RSS(Residual Sum of Squares) 에 L1 penalty term(회귀계수의 절대값의 합) 이 더해진 손실함수를 최소로 하는 회계계수 Beta 추정치를 찾는 것입니다. 람다(λ)는 규제하는 강도를 조절하는 매개변수입니다. 

이 목적함수 식을 선형계획법(Linear Planning) 의 제약조건(constraints, subject to)을 가지는 식으로 변경해서 다시 써보면 아래의 왼쪽 수식과 같습니다. 

* Robert Tibshirani, “Regression Shrinkage and Selection via the Lasso” (1996), Journal of the Royal Statistical Society

페널티 항은 모델에서 일부 특징 가중치를 정확히 0로 축소(shrinks to exactly zero)함으로써 모델 내에서 희소성(sparsity)을 촉진합니다. 이는 모델이 가장 관련성이 높은 특징의 하위 집합을 선택하도록 하고 다른 특징(feature selection)을 무시하도록 만듭니다. 

위의 오른쪽 그림은 튜닝 파라미터 람다를 점점 크게 했을 때 변수별 회귀계수의 값이 어느 순간 정확히 0으로 축소되는 것을 알 수 있습니다. 

LASSO 회귀는 특히 많은 특징이 존재하며 일부가 무관하거나 중복될 수 있는 상황에서 유용합니다. 희소성을 촉진함으로써 LASSO는 특징 선택(Feature Selection)을 도와주며 해석 가능하고 잠재적으로 간단한 모델을 만듭니다. 

요약하면, LASSO 회귀는 L1 Regularization을 사용한 선형 회귀 기술로, 과적합을 방지하고 모델의 특징 가중치에 희소성을 촉진하여 더 나은 일반화 성능을 달성합니다.

3. L2 Regularization (Ridge Regression)

Ridge 회귀 또는 L2 Regularization은 모델의 목적 함수에 패널티 항을 통합하는 선형 회귀 기술입니다. Ridge 회귀의 주요 목적은 선형 회귀 비용 함수의 제곱 계수 합에 페널티 항을 추가함으로써 과적합(Overfitting)을 방지하는 것입니다.

표준 선형 회귀 목적 함수는 예측 값과 실제 값 간의 제곱 차이의 합을 최소화하는 것입니다. 릿지 회귀에서는 이 목적 함수에 페널티 항이 추가되어 수정된 목적은 다음과 같습니다. 

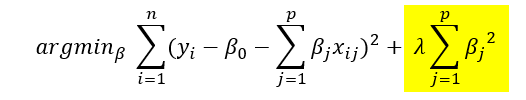
위의 목적함수식을 선형계획법의 제약조건을 가지는 식으로 변경하면 아래와 같습니다. 

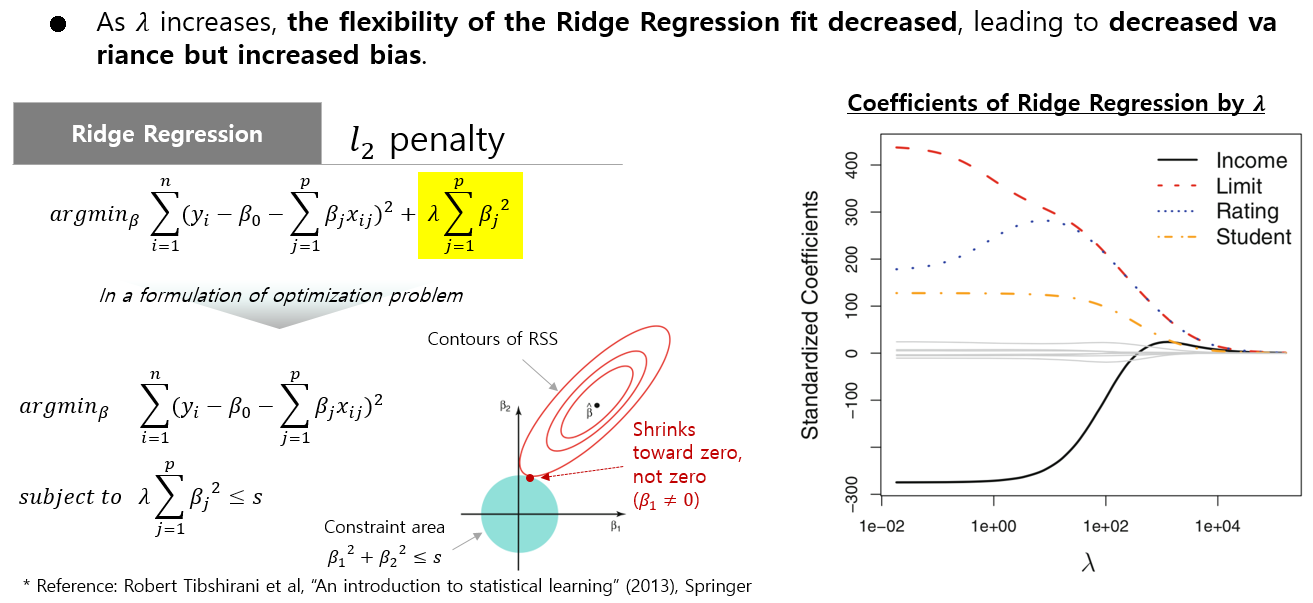
페널티 항은 모델에게 계수를 제로에 가깝게 축소하도록 유도하지만 거의 0으로 만들지는 않습니다.(not exactly zero). 이는 모델이 너무 복잡해지고 훈련 데이터에 과적합되는 것을 방지하는 데 도움이 됩니다.

릿지 회귀는 특징 간에 다중공선성이 있는 경우에 특히 유용하며, 이는 일부 특징이 높은 상관관계를 가질 때 발생합니다. 이러한 경우 릿지 회귀의 정규화 항은 계수를 안정화하고 큰 가중치 값을 피하는 데 도움이 됩니다. 

요약하면, 릿지 회귀는 L2 Regularization을 사용한 선형 회귀 기술로, 제곱 계수의 합에 페널티 항을 추가함으로써 오버피팅을 방지합니다. 이는 훈련 데이터를 잘 맞추는 동시에 모델을 간단하게 유지하고 더 일반적으로 만들기 위한 균형을 제공합니다. 

4. Cross-validation을 이용한 Tuning Parameter Lambda, Mix ratio Gamma 최적값 찾기

Regularization의 강도를 조절하는 튜닝 파라미터 람다(λ)와 Elastic Net 에서 L1, L2 Regularization의 비율을 조절하는 알파(α)는 데이터로 부터 학습될 수 없고 분석가가 지정해줘야 하는 하이퍼-파라미터(Hyper-parameter) 입니다. 

분석 툴에서 제공하는 기본 값을 람다(λ), 알파(α)의 값으로 해도 되지만, 최적의 람다(λ)와 알파(α)를 찾기 위해서는 Cross-validation 기법을 사용합니다. 

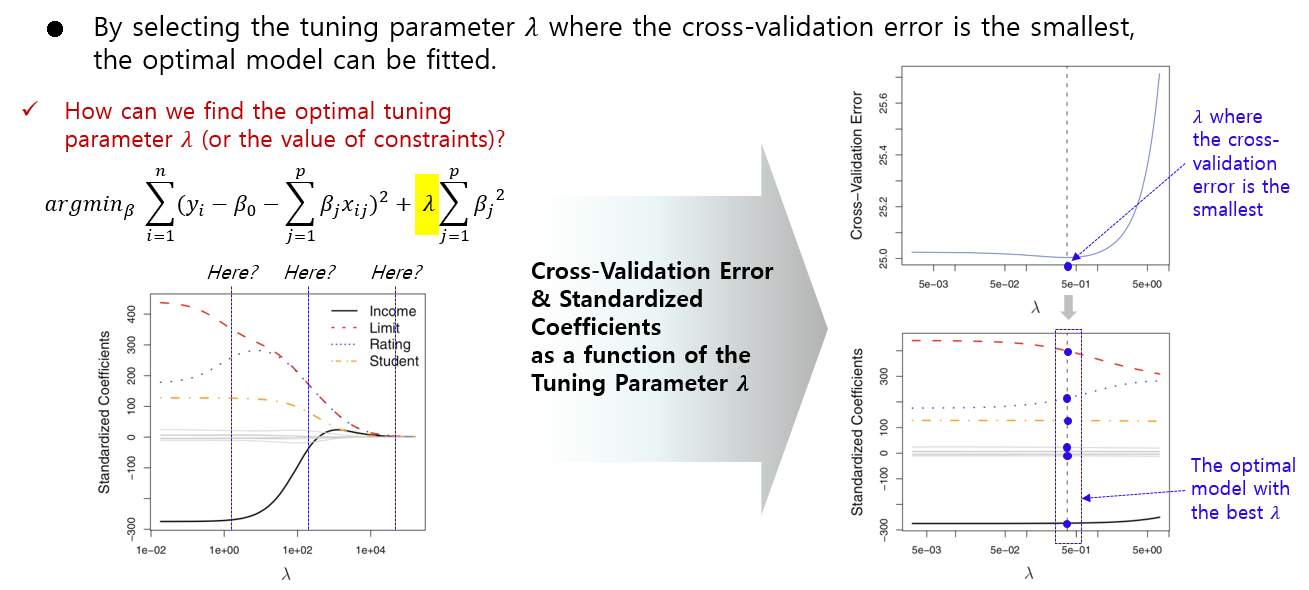
교차 검증(Cross-validation)은 예측 모델의 성능을 평가하고 과적합의 위험을 줄이기 위한 통계적 기술로, 데이터 집합을 여러 하위 집합으로 나누고 모델을 이러한 하위 집합 중 일부로 훈련하고 나머지로 성능을 평가하는 과정을 포함합니다. 주요 아이디어는 훈련 및 테스트에 서로 다른 하위 집합을 사용하여 모델의 성능에 대한 더 견고한 추정을 얻는 것입니다.

가장 일반적인 교차 검증 형식은 k-겹 교차 검증(k-fold cross-validation)으로, 데이터 집합을 k개의 동일한 크기의 폴드로 나눕니다. 모델은 k번 훈련되며 각 훈련에서 k-1개의 폴드를 사용하고 나머지 폴드를 테스트에 사용합니다. 이 프로세스는 k번 반복되며 각 반복에서 다른 폴드가 테스트에 사용됩니다. 성능 메트릭(예: 정확도, 평균 제곱 오차)은 k번의 반복을 통해 평균화되어 모델의 성능을 더 신뢰할 수 있는 추정으로 제공됩니다.

교차 검증은 특히 하이퍼파라미터 튜닝에 유용하며, 이는 머신 러닝 모델에 대한 최적의 하이퍼파라미터 세트를 찾는 목표입니다. 단일 훈련-테스트 분할을 의존하는 대신 교차 검증을 사용하면 모델의 성능을 여러 훈련-테스트 분할에서 평가할 수 있습니다. 이는 데이터가 특정 랜덤 분할에 따라 평가되는 것에 대한 편향을 줄이는 데 도움이 됩니다.

다음은 하이퍼파라미터 튜닝을 위해 교차 검증을 사용하는 단계별 프로세스입니다:

(1) 데이터 분할: 데이터 집합을 훈련 및 테스트 세트로 나눕니다. 훈련 세트는 k-겹으로 나뉩니다.
(2) 하이퍼파라미터 선택: 튜닝하려는 하이퍼파라미터를 지정합니다.
(3) 하이퍼파라미터 그리드 생성: 튜닝할 하이퍼파라미터 값의 그리드를 정의합니다. 이는 주로 그리드 서치(grid search) 또는 랜덤 서치(random search) 기법을 사용하여 수행됩니다.
(4) 교차 검증 수행: 각 하이퍼파라미터 조합에 대해 k-겹 교차 검증을 수행합니다. k-1개의 폴드를 사용하여 모델을 훈련하고 나머지 폴드를 테스트합니다. 이러한 프로세스를 k번 반복하여 각 반복에서 다른 폴드를 테스트로 사용합니다.
(5) 최적의 하이퍼파라미터 선택: k 폴드를 통해 얻은 성능 중 가장 좋은 평균 성능을 가진 하이퍼파라미터 세트를 선택합니다.
(6) 최종 모델 훈련: 선택된 하이퍼파라미터를 사용하여 전체 훈련 세트에서 최종 모델을 훈련합니다.

교차 검증을 사용하여 하이퍼파라미터 튜닝을 수행하면 데이터의 여러 하위 집합에서 어떤 하이퍼파라미터가 잘 작동하는지에 대한 보다 신뢰할 수 있는 평가를 얻을 수 있습니다.

5. Python sklearn을 이용한 LASSO 예제 (w/ Hyperparameter tuning)

Python의 Scikit-learn 모듈에 있는 sklearn.linear_model.Lasso 메소드를 사용해서 LASSO 회귀를 적합해보겠습니다. 이때 GridSearchCV 로 규제의 강도를 조절하는 튜닝 파라미터 alpha (위에서는 람다로 표기, 좀 헷갈릴 수 있겠네요..) 의 최적의 값을 찾아보도록 하겠습니다. 

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import mean_squared_error

# Generate some example data
np.random.seed(42)
x1 = 2 * np.random.rand(100, 1)   # strong relation with y
x2 = 2 * np.random.rand(100, 1) # no relation with y
X = np.column_stack([x1, x2])

y = 4 + 3 * x1 + 0.1 * np.random.randn(100, 1)

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Perform Lasso regression with grid search for alpha
lasso = Lasso()
param_grid = {'alpha': [0.01, 0.1, 0.5, 1.0, 2.0]}  # Values to try for alpha

grid_search = GridSearchCV(lasso, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)

# Get the best hyperparameters
best_alpha = grid_search.best_params_['alpha']

# Train the model with the best hyperparameters
lasso_reg = Lasso(alpha=best_alpha)
lasso_reg.fit(X_train, y_train)

# Read out attributes
coeffs = lasso_reg.coef_            # coefficients
intercept = lasso_reg.intercept_  # intercept

# Make predictions on the test set
y_pred = lasso_reg.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, y_pred)


print(f'Best alpha: {best_alpha}')
print('Coefficients:', coeffs)
print('Intercept:', intercept)
print(f'Mean Squared Error: {mse}')


# Best alpha: 0.01
# Coefficients: [2.95614483 0.00726315]
# Intercept: [4.04106647]
# Mean Squared Error: 0.0066267863966506645

Cross-validation 으로 찾은 최적의 best alpha 는 0.01 이네요. 

Alpha = 0.01 일 때 목표변수 y와 강한 상관성이 있는 변수 x1의 회귀계수는 2.956이고, 목표변수 y와는 아무런 상관이 없는 변수 x2 의 회귀계수는 0.0072 로서 거의 0 으로 축소되었습니다. 

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)

지난번 포스팅에서는 불균형 데이터(imbalanced data)가 무엇이고, 분류 모델링 시 무엇이 문제인지에 대해서 알아보았습니다. --> https://rfriend.tistory.com/773

이번 포스팅부터는 불균형 데이터를 가지고 분류 모델링 시 대처방법에 대해서 몇 번에 나누어서 이론과 Python을 활용한 코드를 소개하겠습니다.  먼저 (3-1) 소수 클래스의 데이터 추가 수집과 (3-2) 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정 부터 시작해볼까요? 

[ 불균형 데이터로 분류 모델링하는 방법 ]
  1. 소수 클래스의 데이터 추가 수집 (Get more minority data) 
  2. 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정 
       (evaluation metrics for imbalanced classification)  

  3. 샘플링 방법 (Sampling methods)
    3-1. Undersampling
      : Random Sampling, Tomek Links
    3-2. Oversampling
      : Resampling, SMOTE, Borderline SMOTE, ADASYN
  4. 비용 또는 가중치 조정 방법 (Cost, Weight)
  5. Outlier detection 방법
      : One-class SVM, Isolation Forest, DBSCAN clustering
  6. 확률 튜닝 알고리즘 (Probability Tuning Algorithms)

1. 소수 클래스의 데이터 추가 수집 (Get more minority data)

만약 소수 집단의 데이터를 추가로 수집하거나 또는 생성할 수 있다면 두 집단의 구성비가 균형을 잡히도록 소수 집단의 개수를 늘리면 되겠습니다. 

하지만, 데이터를 수집하는데는 시간과 비용 (time and cost) 이 소요된다는 점, 상황에 따라서는 소수 데이터의 추가 수집이 불가능하다는 점도 고려를 해야겠습니다. 이런 제약사항 때문에 알고리즘적으로 불균형 데이터 문제를 해결하는 방법을 알아둘 필요가 있습니다. 
(다음번 포스팅부터 소개해요)

2. 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정 
     (evaluation metrics for imbalanced classification)

균형 데이터 (balanced data)에 대한 
 - 분류 모델의 성능 평가 지표에 대한 이론은 https://rfriend.tistory.com/771 를 참고하구요, 
 - Python 을 이용한 분류 모델의 성능 평가 코드는 https://rfriend.tistory.com/772 를 참고하세요. 

불균형 데이터 (imbalanced data)에 대한 분류 모델 평가 지표를 선정하는 데는 
 (a) 범주와 확률 중에서 무엇을 예측하는가? 
 (b) 두 범주가 동등하게 중요한가? 아니면 양성(Positive) 범주가 더 중요한가?
 (c) False Negative, False Positive 가 동등하게 중요한가? 아니면 둘 중 하나가 더 중요한가?
의 질문에 대한 답변 별로 평가 지표가 달라집니다. 
(아래의 ‘불균형 데이터에 대한 이진 분류 모델 평가 지표’ 참조) 

(1) 범주(class labels)를 예측하고, 두 범주가 동등하게 중요하며, 다수 범주가 80~90% 이상으로서 불균형 데이터(imbalanced data)인 경우 

       --> Geometirc-Mean (or G-Mean) 

G-Mean = sqrt(Sensitivity x Specificity)

기하평균 G-Mean 은 다수 집단 (Majority class)과 소수 집단 (Minority class) 간 모두의 분류 성능을 측정하는 지표입니다. 낮은 G-Mean 점수는 비록 음성 사례(negative cases)가 정확하게 분류가 되더라도 양성 사례(positive cases)의 분류는 저조한 성능을 보인다는 뜻입니다. G-Mean 지표는 음성 범주(negative class)의 과적합(over-fitting)을 피하고, 양성 범주(positive class)의 과소 적합(under-fitting)을 피하는데 중요하게 사용됩니다. 

(2) 범주를 예측하고, 두 범주가 동등하게 중요하며, 다수 범주가 80~90% 미만인 균형 데이터(balanced data)는

      --> 정확도(Accuracy) 평가지표를 사용하면 됩니다.

하지만, 불균형 데이터에 대해서 정확도 지표를 사용할 경우 다수 집단 만을 잘 분류하고 소수 집단에 대해서는 제대로 분류를 못해도 높은 정확도 점수가 나오는 문제가 있습니다. 

(3) 범주 (class labels) 를 예측하고, 양성 범주 (Positive class)가 더 중요하며, 

      - False Negative, False Positve 가 동등하게 중요하면 (Sensitivity, Precision이 균형있으면 좋은 모델)   
         --> F1 Score

      - False Negative 가 더 비용이 크면 (Sensitivity가 높으면 좋은 모델)   --> F2 Score

      - False Positive 가 더 비용이 크면  (Precision이 높으면 좋은 모델)       --> F0.5 Score

를 사용합니다. 

F1 Score, F0.5 Score, F2 Score 는 높으면 높을수록 더 좋은 모델로 해석합니다.  

참고로, 두 개의 범주가 바뀌어서 양성(Positive)이 음성(Negative)으로, 음성은 양성으로 바뀐 상태에서 혼돈 매트릭스를 만들어서 F2 Score를 계산하면 Inv F0.5 Score 가 됩니다. [2]

아래는 불균형 데이터에 대한 분류 모델의 혼돈 매트릭스를 3가지 시나리오 별로 가상으로 구성하여, 민감도(Sensitivity), 정밀도(Precision), F1 Score, F0.5 Score, F2 Score 를 계산해본 것입니다. 위 설명을 이해하는데 도움이 되기를 바랍니다. 

(a) F1 Score는 정밀도(Precision)와 민감도(Sensitivity) 의 역수의 산술평균의 역수인 조화평균(Harmonic Mean)으로서, 정밀도와 민감도 간의 균형을 측정합니다. 만약 정밀도나 민감도가 0 이라면 F-Measure 는 0 이됩니다. F1 Score는 False Negative 와 False Positive가 동등하게 중요할 때의 모델 성능지표로 적합합니다. 민감도(Sensitivity)와 정밀도(Precision)이 균형있을 때 F1 Score가 높게 나옵니다. 

(b) 불균형 데이터 (imbalanced data)인 경우에는 F0.5 Score 또는 F2 Score 를 사용하는데요, 비즈니스적으로 중요한 소수 범주(minority class)의 False Negative 가 더 비용(cost)이 크면(즉, Sensitivity가 높은 모델이 더 좋은 모델로서, Sensitiviey에 가중치를 더 줌) F2 Score 를 사용합니다. 예측된 양성이 비록 틀리는 비용을 감수하고서라도, 실제 양성(Positive)을 하나라도 더 분류해내고 싶을 때 F2 Score 지표를 사용합니다. 

(c) 반대로, False Positive 가 비용이 더 크면(즉, (Precision이 높은 모델이 더 좋은 모델로서, Precision에 가중치를 더 줌) F0.5 Score를 모델 성능지표를 선택합니다. 실제 양성을 놓치는 비용을 감수하고서라도, 일단 모델이 양성으로 분류를 했으면 실제로도 양성이기를 바라는 경우에 F0.5 Score 지표를 사용합니다. 

(4) 확률(Probability)을 예측하고, 확률 예측치의 정확도를 평가하고 싶을 때

      --> Brier Score

Brier Score 는 확률 예측치의 정확도(accuracy of probability forecast)를 평가할 때 사용합니다. Brier Score 는 두개의 범주(bianry categories)를 가진 이진 분류(binary classification)의 예측 확률에만 사용할 수 모델 평가지표 입니다. [3]

Brier Score의 수식은 아래와 같이 모든 관측치에 대해서 예측확률과 실제 결과(발생하면 1, 아니면 0)와의 차이의 제곱합(Squared Summation)을 관측치의 개수로 나누어서 구한 ‘평균 제곱합 확률 오차(MSE, Mean Squared Error)’ 입니다. 

Brier Score 는 작으면 작을 수록 이진 분류 모델의 확률 예측치가 정확하다는 뜻이며, 반대로 크면 클 수록 이진 분류 모델의 확률 예측치가 부정확하다고 해석합니다. 

- 모든 확률 예측치에 대해서 완벽하게 모두 다 맞추면 Brier Score 는 0 이 됩니다. (최소값) 
- 반대로, 모든 확률 예측치가 완벽하게 다 틀리면 Brier Score 는 1 이 됩니다. (최대값) 

(5) 확률을 예측하고, 범주가 필요하며, 양성(Positive) 범주가 더 중요한 불균형 데이터의 경우 
   —> Precision-Recall Curve Plot, Precision-Recall AUC (Area Under the Curve)

Precision-Recall Curve 그림은 X축이 Recall, Y축이 Precision으로 해서, 두 범주를 분류하는 확률의 의사결정 기준점(Decision Treshold)을 0에서 1로 조금씩 변경해가면서 혼돈 매트릭스를 계산하고, 이어서 Precision과 Recall을 계산한 후에, 이 값들을 선으로 연결한 그래프입니다. 

아래의 그래프처럼 Precision-Recall Curve 가 우측 상단으로 붙을 수록 불균형 데이터의 양성(Positive)을 더 잘 분류하는 모델이라고 평가할 수 있습니다. (Precision 과 Recall 은 Trade-off 관계에 있음). 

ROC AUC 처럼, Precision-Recall Curve 의 아래 부분의 면적을 적분한 값이 PR AUC (Precision-Recall Area Under the Curve) 값이 됩니다. 하나의 score 로 계산이 되므로, 여러 모델을 수치적으로 비교할 수 있습니다. PR AUC가 크면 클 수록 소수의 양성 범주(minority Positive class) 를 잘 분류하는 모델이라고 평가할 수 있습니다. 

[ Reference ] 

(1) Tour of Evaluation Metrics for Imbalanced Classification
: https://machinelearningmastery.com/tour-of-evaluation-metrics-for-imbalanced-classification/

(2) "F-score" from Wikipedia: https://en.wikipedia.org/wiki/F-score

(3) Brier Score: https://www.statisticshowto.com/brier-score/

앞으로 몇 번의 포스팅으로 나누어서 불균형 데이터 (imbalanced data)에 대해서 다루어보도록 하겠습니다. 

1. 불균형 데이터 (Imbalanced Data) 란 무엇인가? 
2. 불균형 데이터는 분류 모델링 시 무엇이 문제인가? 
3. 불균형 데이터로 분류 모델링하는 방법에는 무엇이 있나? 

1. 불균형 데이터 (Imbalanced Data) 란 무엇인가? 

불균형 데이터 (Imbalanced Data) 는 목표 변수(target/output variable) 가 범주형 데이터 일 때, 범주 별로 관측치의 개수, 비율의 차이가 많이 나는 데이터를 말합니다. 


아래의 각 산업별 예처럼, 정상 대 비정상의 비율이 90%:10% 처럼 불균형하거나, 더 심하면 99%:1% 처럼 극심하게 불균형한 데이터 (extremely imbalanced data) 도 있습니다. 우리가 관심있어하고 예측하고 싶어하는 비정상 관측치가 정상보다 매우 적은 불균형 데이터를 실무에서는 어렵지 않게 볼 수 있습니다. 

  - 제조회사에서 양품 대 불량품
  - 신용카드회사에서 정상 거래 대 사기 거래 (Fraud) 
  - 은행의 정상 거래 대 돈세탁 거래
  - 의료검진센터에서 정상 대 암(cancer) 진단
  - 사이버보안 회사에서 정상 IP 대 비정상 IP 
  - 통신회사에서 유지 고객 대 이탈(Churn) 고객 
  - 설비/장비의 정상 대 이상 운영
  - 유통회사 대리점의 정상 대 비정상 거래

불균형 데이터에서 다수를 차지하는 범주를 ‘다수 범주(majority class)’라고 하고, 적은 수를 차지하는 범주는 ‘소수 범주 (minority class)’ 라고 합니다. 

2. 불균형 데이터는 분류 모델링 (Classification Modeling) 시 무엇이 문제인가? 

불균형 데이터를 가지고 분류 모델을 훈련시키면 우리가 관심있어하는 minority class 를 제대로 분류할 수 없는 쓸모없는 모델이 만들어질 위험이 있습니다. 가령, 정상(majority class) : 비정상(minority class) 의 비율이 99% : 1% 라고 해보겠습니다. 이런 불균형 데이터에 대해 분류 모델을 훈련시킨 후 예측을 하면 모든 데이터를 ‘정상(majority class)’ 이라고 분류한다고 했을 때 정확도(accuracy)는 99%가 됩니다. 얼필 보면 잘 만들어진 모델 같습니다만, 우리가 관심있어하는 ‘비정상(minority class)’ 범주는 하나도 제대로 분류를 해내지 못했으므로 쓸모없는 모델이라고 하는 것입니다. 

또한, 소수 집단(minority class) 의 관측치 개수가 적으면 소수 집단의 모집단 분포를 샘플링한 소수의 관측치가 대표하기에는 부족하므로 분류 모델이 과적합 (overfitting)에 빠질 위험이 있습니다. 그래서 훈련 데이터셋에는 소수 집단을 분류했다고 하더라도, 새로운 데이터에 대해서는 소수 집단을 제대로 분류를 못할 위험이 있습니다. 

3. 불균형 데이터로 분류 모델링하는 방법에는 무엇이 있나? 

아래의 6가지 방법이 있는데요, 3-2번 부터 해서 하나씩 차근차근 이어서 포스팅을 해보겠습니다. 

  3-1. 소수 클래스의 데이터 추가 수집 (Get more minority data) 
  3-2. 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정 
       (evaluation metrics for imbalanced classification)
  3-3. 샘플링 방법 (Sampling methods)
    3-3-1. Undersampling
      : Random Sampling, Tomek Links
    3-3-2. Oversampling
      : Resampling, SMOTE, Borderline SMOTE, ADASYN
  3-4. 비용 또는 가중치 조정 방법 (Cost, Weight)
  3-5. Outlier detection 방법
      : One-class SVM, Isolation Forest, DBSCAN clustering
  3-6. 확률 튜닝 알고리즘 (Probability Tuning Algorithms)

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!   :-)

지난번 포스팅에서는 분류 모델(classification model)의 성능을 평가할 수 있는 지표 (evaluation metrics)에 대해서 소개하였습니다. (https://rfriend.tistory.com/771)

이번 포스팅에서는 Python을 사용하여 예제 데이터에 대해 분류 모델의 성능 평가를 해보겠습니다. 

(1) 예제로 사용할 Breast Cancer 데이터셋을 로딩하고, Data와 Target으로 구분

(2) Training set, Test set 분할

(3) Logistic Regression 모델 적합 (Training)

(4) 예측 (Prediction)

(5) 혼돈 매트릭스 (Confusion Matrix)

(6) 분류 모델 성능 지표: Accuracy, Precision, Recall rate, Specificity, F-1 score

(7) ROC 곡선, AUC 점수

(1) 예제로 사용할 Breast Cancer 데이터셋을 로딩하고, Data와 Target으로 구분 

target의 '0' 이 'malignant (악성 종양)' 이고, '1'은 'benign' 으로서 정상을 의미합니다. 우리는 'malignant (악성 종양)' 을 분류하는 모델에 관심이 있으므로 target '0' 이 'Positive Label' 이 되겠습니다. 

import numpy as np

## load a Iris dataset
from sklearn.datasets import load_breast_cancer

bc = load_breast_cancer()

## target names
bc.target_names
#array(['malignant', 'benign'], dtype='<U9')

## [0: 'malignant'(악성), 1: 'benign']
np.unique(bc['target'], return_counts=True) 
#(array([0, 1]), array([212, 357]))


## getting data, target
bc_data = bc['data']
bc_target = bc['target']

bc_data.shape
#(569, 30)

bc_target[:20]
#array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1])

(2) Training set, Test set 분할

Training set 0.5, Test set 0.5 의 비율로 무작위 추출하여 분할하였습니다. 

## splits training and test set
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    bc_data, 
    bc_target, 
    test_size=0.5,  
    random_state=1004
)

(3) Logistic Regression 모델 적합 (Training)

Traning set을 사용해서 로지스틱 회귀모형을 적합하였습니다.

## training a Logistic Regression model with training set
from sklearn.linear_model import LogisticRegression

clf = LogisticRegression(
    solver='liblinear', 
    random_state=1004).fit(X_train, y_train)

(4) 예측 (Prediction)

Test set에 대해서 예측을 하고 모델 성능 평가를 해보겠습니다. 

predict() 메소드는 범주를 예측하여 반환하고, predict_praba() 메소드는 확률(probability)을 반환합니다. 

## prediction for test set
y_pred = clf.predict(X_test) # class
y_pred_proba = clf.predict_proba(X_test) # probability

실제 범주의 값과 예측한 범주의 값, 그리고 target '0'(malignant, 악성 종양) 일 확률을 DataFrame으로 묶어보았습니다. 

# All in a DataFrame
pred_df = pd.DataFrame({
    'actual_class': y_test, 
    'predicted_class': y_pred, 
    'probabilty_class_0': y_pred_proba[:,0] # malignant (악성)
})

pred_df.head(10)
#    actual_class  predicted_class  probabilty_class_0
# 0             1                1            0.002951
# 1             0                0            0.993887
# 2             0                1            0.108006
# 3             1                1            0.041777
# 4             0                0            1.000000
# 5             0                0            1.000000
# 6             0                0            0.999633
# 7             1                1            0.026465
# 8             0                0            0.997405
# 9             1                1            0.002372

이제 여기서부터 분류 모델의 성능 평가를 시작합니다. 

(5) 혼돈 매트릭스 (Confusion Matrix)

혼돈 매트릭스의 Y축은 Actual 의 malignant (0), benign(1) 이며, X 축은 Predicted 의 malignant (0), benign(1) 입니다. 

## model evaluation
# Confusion matrix
from sklearn.metrics import confusion_matrix

confusion_matrix(y_test, y_pred, 
                 labels=[0, 1]) # 'malignant'(0), 'benign'(1)

#                   predicted
#                   malignant  benign
# actual malignant [[102,       16],
#        benign    [  3,       164]])

(6) 분류 모델 성능 지표: Accuracy, Precision, Recall rate, Specificity, F-1 score

from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_fscore_support

## performance metrics
accuracy = accuracy_score(y_test, y_pred)

precision, recall, fscore, support = \
    precision_recall_fscore_support(y_test, y_pred)

print('Accuracy   : %.3f' %accuracy) # (102+164)/(102+16+3+164)
print('Precision  : %.3f' %precision[0]) # 102/(102+3)
print('Recall     : %.3f' %recall[0]) # 102/(102+16)
print('Specificyty: %.3f' %recall[1]) # 164/(3+164)
print('F1-Score   : %.3f' %fscore[0]) # 2/(1/precision + 1/recall) = 2/(1/0.971+1/0.864)

# Accuracy   : 0.933
# Precision  : 0.971
# Recall     : 0.864
# Specificyty: 0.982
# F1-Score   : 0.915

sklearn의 classification_report() 메소드를 활용해서 한꺼번에 쉽게 위의 분류 모델 성능평가 지표를 계산하고 출력할 수 있습니다. 참고로, 'macro avg' 는 가중치가 없는 평균이며, 'weighted avg'는 support (관측치 개수) 로 가중치를 부여한 평균입니다. 

from sklearn.metrics import classification_report

target_names = ['malignant(0)', 'benign(1)']
print(classification_report(y_test, y_pred, 
                            target_names=target_names))

#               precision    recall  f1-score   support

# malignant(0)       0.97      0.86      0.91       118
#    benign(1)       0.91      0.98      0.95       167

#     accuracy                           0.93       285
#    macro avg       0.94      0.92      0.93       285
# weighted avg       0.94      0.93      0.93       285

(7) ROC 곡선, AUC 점수

ROC 곡선과 AUC 점수는 예측 확률을 이용합니다.

ROC 곡선은 모든 의사결정 기준선 (decision threshold)에 대하여 혼돈 매트릭스를 만들고, X축에는 False Positive Rate(=1-specificity), Y축에는 True Positive Rate (=recall, sensitivity) 의 값을 선그래프로 그린 것이며, 좌측 상단으로 그래프가 붙을 수록 더 잘 적합된 모델이라고 평가합니다. AUC 점수는 ROC 곡선의 아랫부분의 면적을 적분한 값입니다. 

## ROC Curve, AUC
import sklearn.metrics as metrics

fpr, tpr, threshold = metrics.roc_curve(
    y_test, 
    y_pred_proba[:, 0], 
    pos_label=0) # positive label

AUC = metrics.auc(fpr, tpr)

# plotting ROC Curve
import matplotlib.pyplot as plt

plt.figure(figsize = (8, 8))
plt.plot(fpr, tpr, 'b', label = 'AUC = %0.3f' % AUC)
plt.title(('ROC Curve of Logistic Regression'), fontsize=18)
plt.legend(loc = 'lower right')

plt.plot([0, 1], [0, 1],'r--') # random guess
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate', 
                fontsize=14)
plt.xlabel('False Positive Rate', 
                fontsize=14)

plt.show()

[ Reference ] 

1) Breast Cancer Dataset
: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_breast_cancer.html

2) Scikit-Learn Logistic Regression
: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

3) 분류 모델의 성과 평가 지표 : https://rfriend.tistory.com/771

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)

이번 포스팅에서는 분류 모델 (classification model) 의 성능을 비교 평가할 수 있는 지표(evaluation metrics)들에 대해서 소개하겠습니다. 

(1) 혼돈 매트릭스 (Confusion Matrix)

(2) 혼돈 매트릭스 기반 분류 모델 성능 평가 지표

    - 정확도 (Accuracy)

    - 재현율 (Recall rate), 민감도 (Sensitivity)

    - 특이도 (Specificity)

    - 정밀도 (Precision)

    - F-1 점수 (F-1 Score)

(3) 정밀도와 재현율의 상충 관계 (Precision/ Recall Trade-off)

(4) 분류 확률 기반 ROC Curve, AUC (Area Under the ROC Curve)

(5) Python 을 이용한 분류 모델 성능 평가 (다음번 포스팅)

(1) 혼돈 매트릭스 (Confusion Matrix)

먼저 범주의 정답(Y, Label)을 알고 있는 데이터의 실제 값 (Actual) 과 분류 모델을 통해 분류한 예측 값 (Predicted) 을 평가하여 아래와 같은 표의 형태로 객체의 수를 셉니다. Positive 는 '1'/ 'Success'/ 'Pass'/ 'Live' 등에 해당하며, Negative 는 '0'/ 'Fail'/ 'Non Pass'/ 'Dead' 등을 의미합니다. 

TP (True Positive), FP (False Positive), FN (False Negative), TN (True Negative) 는 아래의 표를 보면 의미가 더 명확할거예요. (P와 N은 예측치를 의미하며, 이걸 실제 값과 비교했을 때 맞혔으면 True, 틀렸으면 False 로 표기한 것임)

책에 따라서 '실제 값 (Actual)'과 '예측 값 (Predicted)' 의 축이 다른 경우도 있으니 가로 축과 세로 축이 무엇을 의미하는지 꼭 확인이 필요합니다. 

(2) 혼돈 매트릭스 기반 분류 모델 성능 평가 지표

모든 관측치의 개수를 N (= TP + TN + FP + FN) 이라고 하면, 

    - 정확도 (Accuracy) = (TP + TN) / N

    - 재현율 (recall rate), 민감도 (Sensitivity) = TP / (TP + FN)

    - 특이도 (Specificity) = TN / (FP + TN)

    - 정밀도 (Precision) = TP / (TP + FP)

    - F1 점수 (F1 Score) = 1 / (1/Precision + 1/Recall)

의 수식을 이용해서 구할 수 있습니다. 

F-1 점수 (F-1 Score)는 정밀도와 재현율의 조화평균(harmonic mean, 역수의 산술평균의 역수)으로서, 정밀도와 재현율이 균형있게 둘 다 높을 때 F-1 점수도 높게 나타납니다. 정밀도와 재현율이 모두 중요한 경우에는 F-1 점수를 사용해서 모델을 평가하면 됩니다. 

(3) 정밀도와 재현율의 상충 관계 (Precision/ Recall Trade-off)

정밀도(Precision)와 재현율(Recall rate)은 분류 예측을 위한 의사결정 기준점(decision threshold)을 얼마로 하느냐에 따라 달라집니다. (의사결정 기준점에 따라 혼돈 매트릭스의 4사분면의 각 숫자가 달라짐) 

정밀도와 재현율은 상충 관계에 있어서, 마치 시소 게임처럼 정밀도가 높아지면 재현율이 낮아지고, 반대로 재현율이 높아지면 정밀도는 낮아집니다. 이 상충관계를 잘 이해해야 왜 이렇게 많은 분류 모델 성과평가 지표가 존재하고 필요한지 이해할 수 있습니다. 

보통은 '양성(Positive, 1)' 으로 분류할 확률이 의사결정 기준점 '0.5' 보다 크면 '양성 (Positive, 1)' 로 분류하고, '0.5' 보다 같거나 작으면 '음성 (Negative, 0)' 으로 분류를 합니다. (아래 그림의 (2)번 케이스)

만약 '실제 양성' (Actual Positive) 을 더 많이 잡아내고 싶으면 (실제 음성을 양성으로 오분류할 비용을 감수하고서라도), 의사결정 기준점을 내려주면 됩니다. (아래 그림의 (1)번 케이스) 그러면 재현율(Recall rate)은 올라가고, 정밀도(Precision) 은 낮아집니다. 

만약 '예측한 양성'이 실제로도 양성인 비율 (즉, 정밀도, Precision)을 높이고 싶으면 의사결정 기준점을 올려주면 됩니다. (아래 그림의 (3)번 케이스). 그러면 정밀도(Precision)은 올라가고, 재현율(Recall rate)은 내려가게 됩니다. 

의사결정 기준점을 변경하고 싶다면 비즈니스 목적 상 재현율과 정밀도 중에서 무엇이 더 중요한 지표인지, 실제 양성을 놓쳤을 때의 비용과 예측한 양성이 실제로는 음성이었을 때의 비용 중에서 무엇이 더 끔찍한 것인지를 생각해보면 됩니다. 

가령, 만약 코로나 진단 키트의 분류 모델이라면 '실제 양성 (즉, 코로나 감염)' 인 환자가 '음성'으로 오분류 되어 자가격리 대상에서 제외되고 지역사회에 코로나를 전파하는 비용이 '실제 음성 (즉, 코로나 미감염)' 인 사람을 '양성'으로 오분류했을 때보다 비용이 더 크다고 할 수 있으므로 (1) 번 케이스처럼 의사결정 기준점을 내려서 재현율(Recall rate)을 올리는게 유리합니다. 

반면, 유튜브에서 영유아용 컨텐츠 적격 여부를 판단하는 분류모델을 만든다고 했을 때는, 일단 분류모델이 '영유아용 적격 판단 (Positive)' 을 내련 영상 컨텐츠는 성인물/폭력물/욕설 등의 영유아용 부적격 컨텐츠가 절대로 포함되어 있으면 안됩니다. 이럴경우 일부 실제 영유아용 적격 컨텐츠가 '부적격'으로 오분류되는 비용을 감수하고서라도 (3)번 케이스처럼 의사결정 기준점을 올려서 정밀도를 높게 해주는 것이 유리합니다. 

그리고, 극도로 불균형한 데이터셋 (extremely imbalanced dataset) 의 경우 정확도(Accuracy) 지표는 모델을 평가하는 지표로 부적절합니다. 이때는 비즈니스 목적에 맞게 재현율과 정밀도 중에서 선택해서 사용하는 것이 필요합니다. (양성이 희소한 경우 모델이 모두 음성이라고 예측해도 정확도 지표는 매우 높게 나옴. 하지만 우리는 희소한 양성을 잘 찾아내는 모델을 원하지 모두가 다 음성이라고 예측하는 쓸모없는 모델을 원하지는 않음.)

(4) 분류 확률 기반 ROC Curve, AUC (Area Under the ROC Curve)

ROC 곡선(Receiver Operating Characteristic Curve)은 모든 분류 의사결정 기준값(decision threshold)에서 분류 모델의 성능을 보여주는 그래프입니다. X축은 False Positive Rate, Y축은 True Positive Rate 으로 하여 모든 의사결정 기준값 (Positive 일 확률) 별로 혼돈 매트릭스를 구하고, 여기에서 재현율과 특이도를 구해서 TPR과 FPR을 구하고, 이를 선으로 연결해주면 됩니다. 

ROC 곡선은 45도 대각선이 무작위로 추측하여 분류했을 때를 의미하며, ROC 곡선이 좌측 상단으로 붙으면 붙을 수록 분류 모델의 성능이 더 좋다고 해석합니다. (False Positive Rate 보다 True Positive Rate이 상대적으로 더 높을 수록 더 좋은 분류 모델임)

AUC (Area Under the ROC Curve) 점수는 위의 ROC 곡선의 아랫 부분을 적분하여 하나의 수치로 분류 모델의 성능을 표현한 것입니다. AUC 점수가 높으면 높을 수록 더 좋은 분류 모델입니다.  

ROC 곡선과 AUC 모두 분류 모델이 '양성일 확률(probability)'을 반환할 때만 계산이 가능합니다.

(즉, 모델이 분류할 범주(category, class)로 예측값을 반환하면 ROC 곡선, AUC 계산 불가)

다음번 포스팅에서는 Python을 이용한 분류모델 성능 평가를 해보겠습니다. 

(https://rfriend.tistory.com/772)

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)

지난번 포스팅에서는 차원 축소란 무엇이고 왜 하는지(https://rfriend.tistory.com/736)와 투영(projection) 방법을 사용하는 주성분 분석(PCA)을 통한 차원 축소 (https://rfriend.tistory.com/751) 에 대해서 소개하였습니다. 

이번 포스팅에서는 manifold learning approche 에 해당하는 비지도학습, 비선형 차원축소 방법으로서 LLE (Locally Linear Embedding) 알고리즘을 설명하겠습니다. 

(1) 매니폴드 학습 (Manifold Learning)

(2) Locally Linear Embedding (LLE) 알고리즘

(3) sklearn 을 사용한 LLE 실습

(1) 매니폴드 학습 (Maniflod Learning)

먼저 매니폴드 학습(Manifold Learning)에 대해서 간략하게 살펴보고 넘어가겠습니다.

매니폴드란 각 점 근처의 유클리드 공간과 국부적으로 유사한 위상 공간을 말합니다. (A manifold is a topological space that locally resembles Eucludian space near each point.) [1]  d-차원의 매니폴드는 n-차원 공간 (이때 d < n) 의 부분으로서 d-차원의 초평면(d-dimensional hyperplane)을 국부적으로 닮았습니다. 아래의 3차원 공간의 Swiss Roll 에서 데이터의 구성 특성과 속성을 잘 간직한 2차원의 평면(plane)을 생각해볼 수 있는데요, Swiss Roll 을 마치 돌돌 말린 종이(매니폴드)를 펼쳐서 2차원 공간으로 표현해본 것이 오른쪽 그림입니다. 

매니폴드 학습(Manifold Learning)이란 데이터에 존재하는 매니폴드를 모델링하여 차원을 축소하는 기법을 말합니다. 매니폴드 학습은 대부분 실세계의 고차원 데이터가 훨씬 저차원의 매니폴드에 가깝게 놓여있다는 매니폴드 가정(Manifold Assumption) 혹은 매니폴드 가설(Maniflod Hypothesis)에 기반하고 있습니다. [2] 

위의 비선형인 3차원 Swiss Roll 데이터를 선형 투영 기반의 주성분 분석(PCA, Principal Component Analysis)이나 다차원척도법(MDS, Multi-Dimensional Scaling) 로 2차원으로 차원을 축소하려고 하면 데이터 내 존재하는 매너폴드를 학습하지 못하고 데이터가 뭉개지고 겹쳐지게 됩니다. 

매니폴드 가설은 분류나 회귀모형과 같은 지도학습을 할 때 고차원의 데이터를 저차원의 매니폴드 공간으로 재표현했을 때 더 간단하고 성과가 좋을 것이라는 묵시적인 또 다른 가설과 종종 같이 가기도 합니다. 하지만 이는 항상 그런 것은 아니며, 데이터셋이 어떻게 구성되어 있느냐에 전적으로 의존합니다. 

(2) Locally Linear Embedding (LLE) 알고리즘

LLE 알고리즘은 "Nonlinear Dimensionality Reduction by Locally Linear Embedding (2000)" [3] 논문에서 주요 내용을 간추려서 소개하겠습니다. 

LLE 알고리즘은 주성분분석이나(PCA) 다차원척도법(MDS)와는 달리 광범위하게 흩어져있는 데이터 점들 간의 쌍을 이룬 거리를 추정할 필요가 없습니다. LLE는 국소적인 선형 적합으로 부터 전역적인 비선형 구조를 복원합니다 (LLE revocers global nonlinear structure from locally linear fits.). 

논문에서 소개한 LLE 3단계 절차(steps of locally linear embedding)는 꽤 간단합니다. 

    (1단계) 각 데이터 점의 이웃을 선택 (Select neighbors)

    (2단계) 이웃으로부터 선형적으로 가장 잘 재구성하는 가중치를 계산 (Reconstruct with linear weights)

    (3단계) 가중치를 사용해 저차원의 임베딩 좌표로 매핑 (Map to embedded coordinates)

1단계에서 각 데이터 점별로 이웃을 할당할 때는 데이터 점들 간의 거리를 계산하는데요, 가령 K 최근접이웃(K nearest neighbors) 기법을 사용할 수 있습니다. 

2단계에서 각 데이터 점들의 이웃들로부터 각 점을 가장 잘 재구성하는 선형 회귀계수(linear coefficients, linear weights)를 계산해서 국소적인 기하 특성을 간직한 매너폴드를 학습합니다.  아래는 재구성 에러를 측정하는 비용함수인데요, 원래의 데이터점과 이웃들로 부터 계산한 선형 모형으로 재구성한 값과의 거리를 제곱하여 모두 더한 값입니다. 

위의 비용함수를 최소로 하는 가중치 벡터 Wij 를 계산하게 되는데요, 이때 2가지 제약조건(constraints)이 있습니다. 

  - (a) 각 데이터 점은 단지 그들의 이웃들로 부터만 재구성됩니다.

          (만약 Xj 가 Xi의 이웃에 속하지 않는 데이터점이면 가중치 Wij = 0 이 됩니다.)

  - (b) 가중치 행렬 행의 합은 1이 됩니다. (sum(Wij) = 1) 

위의 2가지 제약조건을 만족하면서 비용함수를 최소로 하는 가중치 Wij 를 구하면 특정 데이터 점에 대해 회전(rotations), 스케일 조정(recalings), 그리고 해당 데이터 점과 인접한 데이터 점의 변환(translations) 에 있어 대칭(symmetry)을 따릅니다. 이 대칭에 의해서 (특정 참조 틀에 의존하는 방법과는 달리) LLE의 재구성 가중치는 각 이웃 데이터들에 내재하는 고유한 기하학적 특성(저차원의 매너폴드)을 모델링할 수 있게됩니다. 

3단계에서는 고차원(D) 벡터의 각 데이터 점 Xi 를 위의 2단계에서 계산한 가중치를 사용하여 매니폴드 위에 전역적인 내부 좌표를 표현하는 저차원(d) 벡터 Yi 로 매핑합니다.  이것은 아래의 임베팅 비용 함수를 최소로 하는 저차원 좌표 Yi (d-mimensional coordinates) 를 선택하는 것으로 수행됩니다. 

임베팅 비용 함수는 이전의 선형 가중치 비용함수와 마찬가지로 국소 선형 재구성 오차를 기반으로 합니다. 하지만 여기서 우리는 Yi 좌표를 최적화하는 동안 선형 가중치 Wij 를 고정합니다. 임베팅 비용 함수는 희소 N x N 고유값 문제(a sparse N X N eignevalue problem)를 풀어서 최소화할 수 있습니다. 이 선형대수 문제를 풀면 하단의 d차원의 0이 아닌 고객벡터는 원점을 중심으로 정렬된 직교 좌표 집합을 제공합니다. 

LLE 알고리즘은 희소 행렬 알고리듬(sparse matrix algorithms)을 활용하기 위해 구현될 때 비선형 차원축소 기법 중 하나인 Isomap 보다 더 빠른 최적화와 많은 문제에 대해 더 나은 결과를 얻을 수 있는 몇 가지 장점이 있습니다. [4]

아래에 3차원 Swiss Roll 데이터를 여러가지 비선형 차원 축소 기법을 사용해서 적용한 결과인데요 [5], LLE 는 수행 시간이 짧은 장점이 있지만 매니폴드가 약간 찌그러져 있는 한계가 있는 반면에, Isomap과 Hessian LLE 는 국지적인 데이터 형상과 관계를 잘 재표현한 저차원 매니폴드를 잘 잡아내지만 수행 시간이 LLE 대비 굉장히 오래걸리는 단점이 있습니다. 

(3) sklearn 을 사용한 LLE 실습

먼저 sklearn 모듈의 make_swiss_roll 메소드를 사용해서 데이터 점 1,000개를 가지는 3차원의 Swiss Roll 샘플 데이터셋을 만들어보겠습니다. X 는 데이터 점이고, t는 매니폴드 내 점의 주 차원에 따른 샘플의 단변량 위치입니다. 

## Swiss Roll sample dataset
## ref: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_swiss_roll.html
from sklearn.datasets import make_swiss_roll

X, t = make_swiss_roll(n_samples=1000, noise=0.1, random_state=1004)


## X: The points.
X[:5]
# array([[ 1.8743272 , 18.2196214 , -4.75535504],
#        [12.43382272, 13.9545544 ,  2.91609936],
#        [ 8.02375359, 14.23271056, -8.67338106],
#        [12.23095692,  2.37167446,  3.64973091],
#        [-8.44058318, 15.47560926, -5.46533069]])


## t: The univariate position of the sample according to the main dimension of the points in the manifold.
t[:10]
# array([ 5.07949952, 12.78467229, 11.74798863, 12.85471755,  9.99011767,
#         5.47092408,  6.89550966,  6.99567358, 10.51333994, 10.43425738])

다음으로 sklearn 모듈에 있는 LocallyLinearEmbedding 메소드를 사용해서 위에서 생성한 Swiss Roll 데이터에 대해 LLE 알고리즘을 적용하여 2차원 데이터로 변환을 해보겠습니다. 

## Manifold Learning
from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)

X_reduced_lle = lle.fit_transform(X)

X_reduced_lle[:10]
# array([[-0.0442308 ,  0.0634603 ],
#        [ 0.04241534,  0.01060574],
#        [ 0.02712308,  0.01121903],
#        [ 0.04396569, -0.01883799],
#        [ 0.00275144,  0.01550906],
#        [-0.04178513,  0.05415933],
#        [-0.03073913,  0.023496  ],
#        [-0.02880368, -0.0230327 ],
#        [ 0.0109238 , -0.02566617],
#        [ 0.00979253, -0.02309815]])

마지막으로 matplotlib 모듈을 사용해서 2차원 평면에 위에서 LLE 로 매핑한 데이터를 시각화해보겠습니다. 색깔을 t 로 구분하였습니다. 

## 2D Scatter Plot
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = (8, 8)
plt.scatter(X_reduced_lle[:, 0], X_reduced_lle[:, 1], c=t, cmap=plt.cm.hot)
plt.title("Unrolled Swiss Roll by LLE", fontsize=20)
plt.xlabel("$y_1$", fontsize=14)
plt.ylabel("$y_2$", fontsize=14)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)

plt.show()

[Reference]

[1] Wikipedia, "Manifold", https://en.wikipedia.org/wiki/Manifold

[2] Aurelien Geron, "Hands-On Machine Learning with Scikit-Learn & Tensorflow"

[3] Sam T. Roweis, Lawrence K. Saul, "Nonlinear Dimensionality Reduction by Locally Linear Embedding"

[4] Wikipedia, "Nonlinear Dimensionality Reduction",  https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction

[5] Nik Melchior, "Manifold Learning, Isomap and LLE":  https://www.cs.cmu.edu/~efros/courses/AP06/presentations/melchior_isomap_demo.pdf 

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)

지난 포스팅에서는 차원 축소란 무엇이고 왜 하는지, 무슨 방법이 있는지에 대해서 알아보았습니다.

(https://rfriend.tistory.com/736)  차원축소하는 방법에는 크게 Projection-based dimensionality reduction, Manifold Learning 의 두가지 방법이 있다고 했습니다. 

이번 포스팅에서는 투사를 통한 차원축소 방법(dimensionality reduction via projection approach) 으로서 주성분분석을 통한 차원축소(dimensionality reduction using PCA, Principal Component Analysis)에 대해서 소개하겠습니다. 

(1) 주성분분석(PCA, Principal Component Analysis)을 통한 차원 축소

(2) 특이값 분해 (SVD, Singular Value Decomposition)을 통한 차원 축소

(1) 주성분 분석(PCA, Principal Component Analysis)을 통한 차원 축소

주성분 분석(PCA)의 핵심 아이디어만 간략하게 소개하자면요, 피쳐 공간(Feature Space)에서 데이터의 분산을 최대로 잡아낼 수 있는 축을 제1 주성분 축으로 잡고, 이 제1 주성분 축과 직교(orthogonal)하는 축을 제2 주성분 축으로 잡고, ..., 이렇게 최대 변수의 개수 p 개 만큼 주성분 축을 잡아줍니다. (물론, 차원축소를 하는 목적이면 주성분 개수 m 이 변수 개수 p 보다는 작아야 겠지요). 그리고 축을 회전시켜주면 돼요. 

아래의 예시 도면을 보면 파란색 제 1 주성분 축 (1st principal component axis)이 데이터 분산을 가장 많이 설명하고 있는 것을 알 수 있습니다. 빨간색 점선의 제 2 주성분 축(2nd principal component axis) 은 제1 주성분 축과 직교하구요. 

이제 Python 을 가지고 실습을 해볼께요. 

(R로 주성분 분석 하는 것은 https://rfriend.tistory.com/61 를 참고하세요.)

먼저 예제로 사용할 iris 데이터셋을 가져오겠습니다. sepal_length, sepal_width, petal_length, petal_width 의 4개 변수를 가진 데이터셋인데요, 4개 변수 간 상관관계 분석을 해보니 상관계수가 0.8 이상으로 꽤 높게 나온 게 있네요. 주성분분석으로 차원축소 해보면 이쁘게 나올거 같아요. 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

## loading IRIS dataset
from sklearn.datasets import load_iris
data = load_iris()


data['data'][:10]
# array([[5.1, 3.5, 1.4, 0.2],
#        [4.9, 3. , 1.4, 0.2],
#        [4.7, 3.2, 1.3, 0.2],
#        [4.6, 3.1, 1.5, 0.2],
#        [5. , 3.6, 1.4, 0.2],
#        [5.4, 3.9, 1.7, 0.4],
#        [4.6, 3.4, 1.4, 0.3],
#        [5. , 3.4, 1.5, 0.2],
#        [4.4, 2.9, 1.4, 0.2],
#        [4.9, 3.1, 1.5, 0.1]])


## converting into pandas DataFrame
iris_df = pd.DataFrame(
    data['data'], 
    columns=['sepal_length', 'sepal_width', 
             'petal_length', 'petal_width'])

iris_df.head()
# 	sepal_length	sepal_width	petal_length	petal_width
# 0	5.1	3.5	1.4	0.2
# 1	4.9	3.0	1.4	0.2
# 2	4.7	3.2	1.3	0.2
# 3	4.6	3.1	1.5	0.2
# 4	5.0	3.6	1.4	0.2


## correlation matrix
iris_df.corr()
# 	sepal_length	sepal_width	petal_length	petal_width
# sepal_length	1.000000	-0.117570	0.871754	0.817941
# sepal_width	-0.117570	1.000000	-0.428440	-0.366126
# petal_length	0.871754	-0.428440	1.000000	0.962865
# petal_width	0.817941	-0.366126	0.962865	1.000000

주성분 분석은 비지도 학습 (Unsupervised Learning) 이다보니 정답이라는게 없습니다. 그래서 분석가가 주성분의 개수를 지정해주어야 하는데요, 주성분의 개수가 적을 수록 차원 축소가 많이 되는 반면 정보 손실(information loss)가 발생하게 되며, 반면 주성분 개수가 많을 수록 정보 손실은 적겠지만 차원 축소하는 의미가 퇴색됩니다. 그래서 적절한 주성분 개수를 선택(hot to decide the number of principal components)하는게 중요한데요, 주성분의 개수별로 설명 가능한 분산의 비율 (percentage of explained variance by principal components) 을 많이 사용합니다. 

아래의 예에서는 첫번째 주성분이 분산의 92.4%를 설명하고, 두번째 주성분이 분산의 5.3%를 설명하므로, 주성분 1 & 2 까지 사용하면 전체 분산의 97.7%를 설명할 수 있게 됩니다. (즉, 원래 4개 변수를 2개의 차원으로 축소하더라도 분산의 97.7%를 설명 가능하다는 뜻) 

참고로, 만약 주성분분석 결과를 지도학습(가령, 회귀분석)의 설명변수 인풋으로 사용한다면, cross validation을 사용해서 주성분 개수별로 모델의 성능을 평가(가령, 회귀분석의 경우 MSE)해서, 모델 성능지표가 가장 좋은 주성분 개수를 선택하는 것도 좋은 방법입니다. 

## how to decide the number of Principal Components
from sklearn.decomposition import PCA

pca = PCA(random_state=1004)
pca.fit_transform(iris_df)


## percentage of variance explained
print(pca.explained_variance_ratio_)
# [0.92461872 0.05306648 0.01710261 0.00521218]


## Principal 1 & 2 explain about 97.8% of variance
plt.rcParams['figure.figsize'] = (7, 7)
plt.plot(range(1, iris_df.shape[1]+1), pca.explained_variance_ratio_)
plt.xlabel("number of Principal Components", fontsize=12)
plt.ylabel("% of Variance Explained", fontsize=12)
plt.show()

이제 주성분 개수를 2개로 지정(n_components=2)해서 주성분 분석을 실행해보겠습니다. Python의 sklearn 모듈의 decomposition.PCA 메소드를 사용하겠습니다. 

## Dimensionality Reduction with n_components=2
pca = PCA(n_components=2, random_state=1004)
iris_pca = pca.fit_transform(iris_df)


iris_pca[:10]
# array([[-2.68412563,  0.31939725],
#        [-2.71414169, -0.17700123],
#        [-2.88899057, -0.14494943],
#        [-2.74534286, -0.31829898],
#        [-2.72871654,  0.32675451],
#        [-2.28085963,  0.74133045],
#        [-2.82053775, -0.08946138],
#        [-2.62614497,  0.16338496],
#        [-2.88638273, -0.57831175],
#        [-2.6727558 , -0.11377425]])

위에서 실행한 주성분분석 결과를 가지고 시각화를 해보겠습니다. 4개 변수를 2개의 차원으로 축소를 했기 때문에 2차원의 산점도로 시각화를 할 수 있습니다. 이때 iris 데이터셋의 target 속성정보를 이용해서 붓꽃의 품종별로 색깔과 모양을 달리해서 산점도로 시각화해보겠습니다. 

## Visualization

## target
data['target'][:5]
# array([0, 0, 0, 0, 0])


## mapping target name using numpy vectorization
species_map_dict = {
    0: 'setosa', 
    1: 'versicolor', 
    2: 'virginica'
}

iris_pca_df = pd.DataFrame({
    'pc_1': iris_pca[:, 0], 
    'pc_2': iris_pca[:, 1], 
    'species': np.vectorize(species_map_dict.get)(data['target']) # numpy broadcasting
})


iris_pca_df.head()
# pc_1	pc_2	species
# 0	-2.684126	0.319397	setosa
# 1	-2.714142	-0.177001	setosa
# 2	-2.888991	-0.144949	setosa
# 3	-2.745343	-0.318299	setosa
# 4	-2.728717	0.326755	setosa


import seaborn as sns
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = (7, 7)
sns.scatterplot(
    x='pc_1', 
    y='pc_2',
    hue='species', 
    style='species',
    s=100,
    data=iris_pca_df
)

plt.title('PCA result of IRIS dataset')
plt.xlabel('Principal Component 1', fontsize=14)
plt.ylabel('Principal Component 2', fontsize=14)
plt.show()

(2) 특이값 분해 (SVD, Singular Value Decomposition)을 통한 차원 축소

선형대수의 특이값 분해의 결과로 나오는 U, sigma, V 에서 V 가 주성분 분석의 주성분에 해당합니다.  

특이값 분해(SVD, Singular Value Decomposition)에 대한 이론적인 소개는 https://rfriend.tistory.com/185 를 참고하세요. 

numpy 모듈의 linalg.svd 메소드를 사용하여 특이값 분해를 하려고 할 때 먼저 데이터 표준화(standardization)을 수작업으로 진행해 줍니다. (sklearn 으로 주성분분석을 할 때 sklearn 모듈이 내부적으로 알아서 표준화해서 진행해줌). 

## Standardization first
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(data['data'])


## PCA assumes that the dataset is centered around the origin.
X_centered = data['data'] - data['data'].mean(axis=0)
X_centered[:5]
# array([[-0.74333333,  0.44266667, -2.358     , -0.99933333],
#        [-0.94333333, -0.05733333, -2.358     , -0.99933333],
#        [-1.14333333,  0.14266667, -2.458     , -0.99933333],
#        [-1.24333333,  0.04266667, -2.258     , -0.99933333],
#        [-0.84333333,  0.54266667, -2.358     , -0.99933333]])

웨에서 표준화한 데이터를 numpy 모듈의 linalg.svd 메소드를 사용하여 특이값 분해를 해준 후에, V 를 transpose (T) 해주어서 첫번째와 두번째 열의 값을 가져오면 제1 주성분, 제2 주성분을 얻을 수 있습니다. 

## standard matrix factorization using SVD
U, s, V = np.linalg.svd(X_scaled.T)


## V contains all the principal components
pc_1 = V.T[:, 0]
pc_2 = V.T[:, 1]


## check pc_1, pc_2
pc_1[:10]
# array([0.10823953, 0.09945776, 0.1129963 , 0.1098971 , 0.11422046,
#        0.099203  , 0.11681027, 0.10671702, 0.11158214, 0.10439809])


pc_2[:10]
# array([-0.0409958 ,  0.05757315,  0.02920003,  0.05101939, -0.0552418 ,
#        -0.12718049, -0.00406897, -0.01905755,  0.09525253,  0.04005525])

위에서 특이값분해(SVD)로 구한 제1 주성분, 제2 주성분을 가지고 산점도를 그려보겠습니다. 이때 iris 의 target 별로 색깔과 모양을 달리해서 시각화를 해보겠습니다. 

## Visualization

iris_svd_df = pd.DataFrame({
    'pc_1': pc_1, 
    'pc_2': pc_2, 
    'species': np.vectorize(species_map_dict.get)(data['target']) # numpy broadcasting
})


import seaborn as sns
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = (7, 7)
sns.scatterplot(
    x='pc_1', 
    y='pc_2',
    hue='species', 
    style='species',
    s=100,
    data=iris_svd_df
)

plt.title('SVD result of IRIS dataset')
plt.xlabel('Principal Component 1', fontsize=14)
plt.ylabel('Principal Component 2', fontsize=14)
plt.show()

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요. 

이번 포스팅에서는 정답 레이블 Y는 없고 오직 설명변수 X 만을 사용해서 데이터 내 관계, 패턴, 구조를 탐색하는데 사용하는 비지도학습 중에서 차원 축소 (Dimensionality Reduction) 에 대한 이론적인 부분을 알아보겠습니다. (Python 코딩은 다음번 포스팅부터 해볼께요.)

1. 차원 축소란 무엇인가? (What is Dimensionality Reduction?)

2. 왜 차원 축소가 필요한가? (Why is Dimensionality Reduction?) 

3. 차원 축소의 단점은? (Pitfall of Dimensionality Reduction)

4. 차원 축소하는 방법은? (How to do Dimensionality Reduction?)

1. 차원 축소란 무엇인가? (What is Dimensionality Reduction?)

차원 축소 (Dimensionality Reduction, 또는 Dimension Reduction) 는 저차원 표현(low-dimensional representation)이 고차원 원본 데이터의 의미 있는 특성을 이상적으로 원래의 차원에 가깝게 유지할 수 있도록 고차원 공간에서 저차원 공간으로 데이터를 변환(the transformation of data from a high-dimensional space into a low-dimensional space)하는 것을 말합니다.[wikipedia, 1]

차원 축소를 하게 되면 원본 데이터로부터 일부 정보 손실 (information loss)이 발생하는데요, 원본 데이터로부터의 정보 손실을 최소화하면서 저차원으로 얼마나 잘 재표현(representation)할 수 있느냐가 관건이 되겠습니다. 

[ 차원 축소 (Dimensionality Reduction) vs. 군집 분석 (Clustering) ]

차원 축소 (Dimensionality Reduction)와 군집분석 (Clustering) 모두 정답 Label Y 가 필요없이 특성 변수(features) 만을 가지고 데이터의 구조와 특성을 파악하는 비지도학습(Unsupervised Learning) 에 속합니다. 

군집분석 (Clustering) 은 관측치, 객체 간의 유사성(similarity)을 측정해서 유사한 관측치, 객체끼리 그룹을 만드는 분석 기법을 말합니다. 반면에 차원 축소 (Dimensionality Reduction) 는 특성 변수(features, variables)를 대상으로 변수 간 상관성에 기초해서 고차원에서 저차원 공간으로 재표현하는 변수 변환을 말합니다. 

2. 왜 차원 축소가 필요한가? (Why is Dimensionality Reduction?) 

차원 축소를 하는 이유, 활용 목적에는 여러가지가 있는데요, 먼저 기계학습 측면에서는 차원 축소가 차원의 저주 (Curse of Dimensionality)를 피하고, 과적합 (Overfitting) 을 방지하는데 효과적입니다. 

차원의 저주(Curse of Dimensionality) 는 일상적 경험의 3차원 물리적 공간 등 저차원적 환경에서 일어나지 않는 고차원적 공간에서 데이터를 분석하고 정리할 때 발생하는 다양한 현상을 말합니다. 이 표현은 Richard E. Bellman 이 동적 프로그래밍의 문제를 고려할 때 처음 사용하였습니다. 차원 저주 현상은 수치 분석, 샘플링, 조합론, 기계 학습, 데이터 마이닝 및 데이터베이스와 같은 영역에서 발생합니다. 이러한 문제의 공통 주제는 차원성이 증가하면 공간의 부피가 너무 빠르게 증가하여 사용 가능한 데이터가 희박해진다는 것입니다. 신뢰할 수 있는 결과를 얻기 위해 필요한 데이터의 양은 차원성에 따라 기하급수적으로 증가하는 경우가 많습니다. 또한 데이터를 구성하고 검색하는 것은 종종 객체가 유사한 속성을 가진 그룹을 형성하는 영역을 감지하는 데 의존합니다. 그러나 고차원 데이터에서는 모든 객체가 여러 면에서 희박하고 유사하지 않아 일반적인 데이터 구성 전략이 효율적이지 못하게 됩니다. [wikipedia, 2]

통계학의 선형회귀모형에는 독립변수(independent variable, 혹은 설명변수 explanatory variable, 혹은 예측변수 predictor variable) 들 간의 독립을 가정합니다. (독립변수라는 이름 자체에 변수 간 독립을 명시함. ㅎㅎ)  그런데 모델링에 인풋으로 사용하는 설명변수 간 다중공선성(multicolleniarity)이 존재할 경우 추정된 회귀계수의 분산이 커져서 모델이 불안정하고 과적합에 빠지는 위험이 있습니다. 독립변수간 다중공선성(multicolleniarity)을 해결하는 몇가지 방법 중의 하나가 독립변수간 상관성에 기반해서 차원을 축소한 후에 회귀모형을 적합하는 방법입니다. 

탐색적 데이터 분석을 하는 단계에서 변수 간 관계를 파악하기 위해서 산점도(scatter plot)으로 시각화(visualization) 해서 보면 효과적인데요, 만약 특성변수(features)의 개수가 여러개일 경우에는 2개 특성변수 간 조합의 개수가 기하급수적으로 늘어나기 때문에 모든 조합을 시각화해서 살펴보는 것에 어려움이 있습니다.  이럴 경우, 차원축소를 해서 소수의 차원에 대해서 시각화를 하면 많은 양의 정보를 효과적으로 시각화해서 데이터 특성을 탐색해볼 수 있습니다. 

이밖에도 차원 축소를 하면 이후의 데이터 처리, 분석 시에 연산 속도를 향상(performance incease)시킬 수 있습니다. 그리고 데이터를 압축(data compression)하여 데이터 저장이나 전송 효율을 높이는데도 차원 축소를 사용할 수 있습니다. 

3. 차원 축소의 단점은? (Pitfall of Dimensionality Reduction)

차원 축소를 하게 되면 원본 데이터 대비 정도의 차이일 뿐 필연적으로 정보 손실 (Information Loss) 이 발생합니다. 그리고 원본 데이터 대비 차원 축소한 데이터를 해석하는데도 어려움이 (hard to interprete) 생깁니다. 또한 차원 축소를 위한 데이터 변환 절차가 추가되므로 데이터 파이프 라인 (data pipeline) 이 복잡해지는 단점도 있습니다. 

4. 차원 축소하는 방법은? (How to do Dimensionality Reduction?)

차원 축소하는 방법은 크게 (Linear) Projection 과 (Non-linear) Manifold Learning 의 2가지로 나눌 수 있습니다. 

(4-1) Projection-based Dimensionality Reduction: 주성분분석 (PCA, Principal Component Analysis), 특이값 분해 (Singular Value Decomposition), 요인분석 (Factor Analysis)

(4-2) Manifold Learning: LLE (Locally-Linear Embedding), Isomap, Kernel Principal Component Analysis, Autoencoders, SOM(Self-Organizing Map) 

다음번 포스팅에서는 linear projection 방법 중에서 Python 의 Sklearn 모듈을 활용하여 주성분분석 (PCA, Principal Component Analysis)을 하는 방법을 소개하겠습니다. 

[ Reference ] 

[1] Wikipedia - Dimensionality Reduction: https://en.wikipedia.org/wiki/Dimensionality_reduction

[2] Wikipedia - Curse of Dimensionality: https://en.wikipedia.org/wiki/Curse_of_dimensionality

[3] Wikipedia - Nonlinear Dimensionality Reduction: https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)

데이터 유형별로 여러 단계를 거치는 데이터 전처리와 모델의 학습, 신규 데이터에 대한 예측의 전체 기계학습 워크 플로우를 파이프라인으로 관리하면 워크 플로우 관리를 간소화하고 자동화(workflow automation) 하는데 매우 큰 도움이 됩니다. 

이번 포스팅에서는 Python의 scikit learn 모듈을 사용해서 숫자형과 범주형 변수가 섞여 있는 데이터셋의 데이터 전처리 및 선형회귀모형 모델을 학습하는 전체 파이프라인을 만드는 방법을 소개하겠습니다. 

(1) 숫자형 변수의 결측값 처리 및 표준화하는 데이터 전처리 파이프라인 만들기

(2) 범주형 변수의 원핫인코딩하는 데이터 전처리 파이프라인 만들기

(3) ColumnTransformer 클래스로 숫자형과 범주형 변수 전처리 파이프라인 합치기

(4) 숫자형 & 범주형 데이터 전처리와 선형회귀모형 학습하는 파이프라인 만들기

(5) 모델 학습

(6) 예측 및 모델 성능 평가

먼저, 데이터 전처리 및 모델학습과 파이프라인을 구성하는데 필요한 Python modules 을 불러오겠습니다.  그리고 예제로 사용할 오픈 abalone.data 데이터셋을 가지고 pandas DataFrame을 만들어보겠습니다. 

## Importing modules
import numpy as np
import pandas as pd
from sklearn.compose import ColumnTransformer
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error


## Making a DataFrame by reading abalone data set from URL
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data"
abalone = pd.read_csv(
    url, 
    sep=",", 
    names = ['sex', 'length', 'diameter', 'height', 
             'whole_weight', 'shucked_weight', 'viscera_weight', 
             'shell_weight', 'rings'], 
    header = None)
    
    
abalone.head()
# 	sex	length	diameter	height	whole_weight	shucked_weight	viscera_weight	shell_weight	rings
# 0	M	0.455	0.365	0.095	0.5140	0.2245	0.1010	0.150	15
# 1	M	0.350	0.265	0.090	0.2255	0.0995	0.0485	0.070	7
# 2	F	0.530	0.420	0.135	0.6770	0.2565	0.1415	0.210	9
# 3	M	0.440	0.365	0.125	0.5160	0.2155	0.1140	0.155	10
# 4	I	0.330	0.255	0.080	0.2050	0.0895	0.0395	0.055	7

위의 abalone 데이터셋에서 숫자형 변수(numeric variable)인 "length", "whole_weight" 와 범주형 변수(categorical variable)인 "sex" 의 3개 칼럼을 이용해서 "rings" 를 예측하는 선형회귀모형(linear regression)을 학습시키고, 예측을 해보겠습니다. 

(1) 숫자형 변수의 결측값 처리 및 표준화하는 데이터 전처리 파이프라인 만들기

숫자형 변수(numeric features)에 대해서는

  (1-1) scikit learn 모듈의 SimpleImputer() 클래스를 이용해서 결측값을 "중앙값(median)"으로 대체(imputation) 

  (1-2) scikit learn 모듈의 StandardScaler() 클래스를 이용해서 표준화(standardization) 

하는 단계를 거치는 파이프라인을 만들어보겠습니다. 

콤마로 써주는 부분은 각 단계(step)의 alias 이름이 되겠습니다.  아래의 (5)번에서 전체 파이프라인을 시각화했을 때 콤마로 부연설명해준 alias 이름을 도식화한 파이프라인의 윗부분에서 볼 수 있습니다. 

## (1) for numeric features
num_features = ["length", "whole_weight"]
num_transformer = Pipeline(
    steps = [("imputer", SimpleImputer(strategy="median")), ("scaler", StandardScaler())]
)

(2) 범주형 변수의 원핫인코딩하는 데이터 전처리 파이프라인 만들기

범주형 변수(categorical features)에 대해서는 scikit learn 모듈의 OneHotEncoder() 클래스를 사용해서 각 범주별로 칼럼을 만들어서 해당 범주에 속하면 '1' (hot), 해당 범주에 속하지 않으면 '0' (cold) 으로 인코딩을 해서 기계가 인식할 수 있도록 해주는 단계를 정의하겠습니다. 

(참고로, handle_unknown = "ignore" 옵션은 모델을 학습할 때 학습 데이터셋의 범주형 변수에는 없었던 범주가 예측에 사용하는 새로운 데이터셋에서 나타날 경우 무시하라는 의미입니다.)

## (2) Categorical features
cat_features = ["sex"]
cat_transformer = OneHotEncoder(handle_unknown="ignore")

(3) ColumnTransformer 클래스로 숫자형과 범주형 변수 전처리 파이프라인 합치기

위의 (1) 숫자형 데이터 전처리 단계와 (2) 범주형  데이터 전처리 단계를 정의하는 클래스와 파이프라인을 scikit learn 모듈의 ColumnTransformer() 클래스를 사용해서 숫자형 변수(num_features)와 범주형 변수(cat_features) 별로 매핑하여 하나의 데이터 전처리 파이프라인으로 합쳐보겠습니다. 

## (3) Use ColumnTransformer by selecting column by names
preprocessor = ColumnTransformer(
    transformers = [
        ("num", num_transformer, num_features), 
        ("cat", cat_transformer, cat_features)
    ]
)

(4) 숫자형 & 범주형 데이터 전처리와 선형회귀모형 학습하는 파이프라인 만들기

이번에는 위의 (3)번에서 숫자형과 범주형 데이터 전처리를 하나로 묶은 데이터 전처리 파이프라인에 (4) 선형회귀모형을 적합하는 클래스를 추가해서 파이프라인을 만들어보겠습니다. 

## (4) Append regressor to preprocessing pipeline.
lin_reg = Pipeline(
    steps = [("preporcessor", preprocessor), ("regressor", LinearRegression())]
)

(5) 모델 학습

모델을 학습할 때 사용할 training set (0.8) 과 모델의 성능을 평가할 때 사용할 test set (0.2) 를 0.8:0.2의 비율로 무작위 추출해서 분할해보겠습니다. 

## Split training(0.8) and test set(0.2) randomly
X = abalone[["length", "whole_weight", "sex"]]
y = abalone["rings"]

X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                    test_size=0.2, 
                                                    random_state=1004)

sklean 의 set_config(display="diagram") 을 설정해주면 위의 (1) ~ (4) 에서 정의해준 숫자형 & 범주형 변수 데이터 전처리와 선형회귀모형 적합의 전체 기계학습 워크플로우 파이프라인을 다이어그램으로 시각화해서 볼 수 있습니다. 

참고로, 파이프라인의 각 단계의 박스를 커서로 클릭하면 상세 옵션 설정 내용(예: SimpleImputer 클래스의 경우 strategy='median', OneHotEncoder 클래스의 handle_unknown='ignore' 등) 을 펼쳐서 볼 수 있습니다. 그리고 "num"과 "cat" 부분을 클릭하면 숫자형 변수와 범주형 변수 이름을 확인할 수 있습니다. 

이제 드디어 준비가 다 되었군요.  lin_reg.fit(X_train, y_train) 을 실행하면 (1)~(4)의 전체 워크플로우가 파이프라인을 따라서 순차적으로 실행이 됩니다.  코드가 참 깔끔해졌지요! 

## Display a diagram of Pipelines in Jupyter Notebook
from sklearn import set_config

set_config(display="diagram")

## Fit a Linear Regression model using pipelines
lin_reg.fit(X_train, y_train)

(6) 예측 및 모델 성능 평가

이제 따로 떼어놓았던 test set (0.2) 를 가지고 MAPE (Mean Absolute Percentage Error) 지표를 사용해서 모델의 성능을 평가해보겠습니다. 

lin_reg.predict(X_test) 를 실행하면 앞서 정의했던 (1) ~ (4) 의 숫자형 & 문자형 변수별 데이터 전처리와 모델 예측의 전체 워크 플로우의 파이프라인이 물 흐르듯이 자동으로 알아서 진행이 됩니다.  너무나 신기하고 편리하지요?!  

(파이프라인이 있으면 lin_reg.predict(X_test) 라는 코드 단 한줄이면 되는데요, 만약 위의 (1) ~ (4) 의 과정을 수작업으로 Test set 에 대해서 데이터 전처리해주는 코드를 다시 짠다고 생각을 해보세요. -_-;)

## Define UDF of MAPE(Mean Absolute Percentage Error)
## or sklearn.metrics.mean_absolute_percentage_error() class, which is new in version 0.24.
## : https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_absolute_percentage_error.html#sklearn.metrics.mean_absolute_percentage_error
def MAPE(y_test, y_pred): 
    y_test, y_pred = np.array(y_test), np.array(y_pred) 
    return np.mean(np.abs((y_test - y_pred) / y_test)) * 100
    

## Evaluate performance of a model
y_pred = lin_reg.predict(X_test)

print("MSE: %.2f" % MAPE(y_test, y_pred))
#[out] MSE: 18.68

[ Reference ]

- Column Transformer with Mixed Types
: https://scikit-learn.org/stable/auto_examples/compose/plot_column_transformer_mixed_types.html
- sklearn SimpleImputer
: https://scikit-learn.org/stable/modules/generated/sklearn.impute.SimpleImputer.html
- sklearn StandardScaler
: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html
- sklearn OneHotEncoder
: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html
- sklearn Linear Regression
: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
- sklearn Pipeline
: https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
- sklearn train_test_split
: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
- sklearn mean_squared_error
: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html

이번 포스팅이 많은 도움이 되었기를 바랍니다. 

행복한 데이터 과학자 되세요!  :-)