[Greenplum] PL/Python으로 일원분산분석을 병렬처리하기 (one-way ANOVA in parallel using PL/Python on Greenplum)
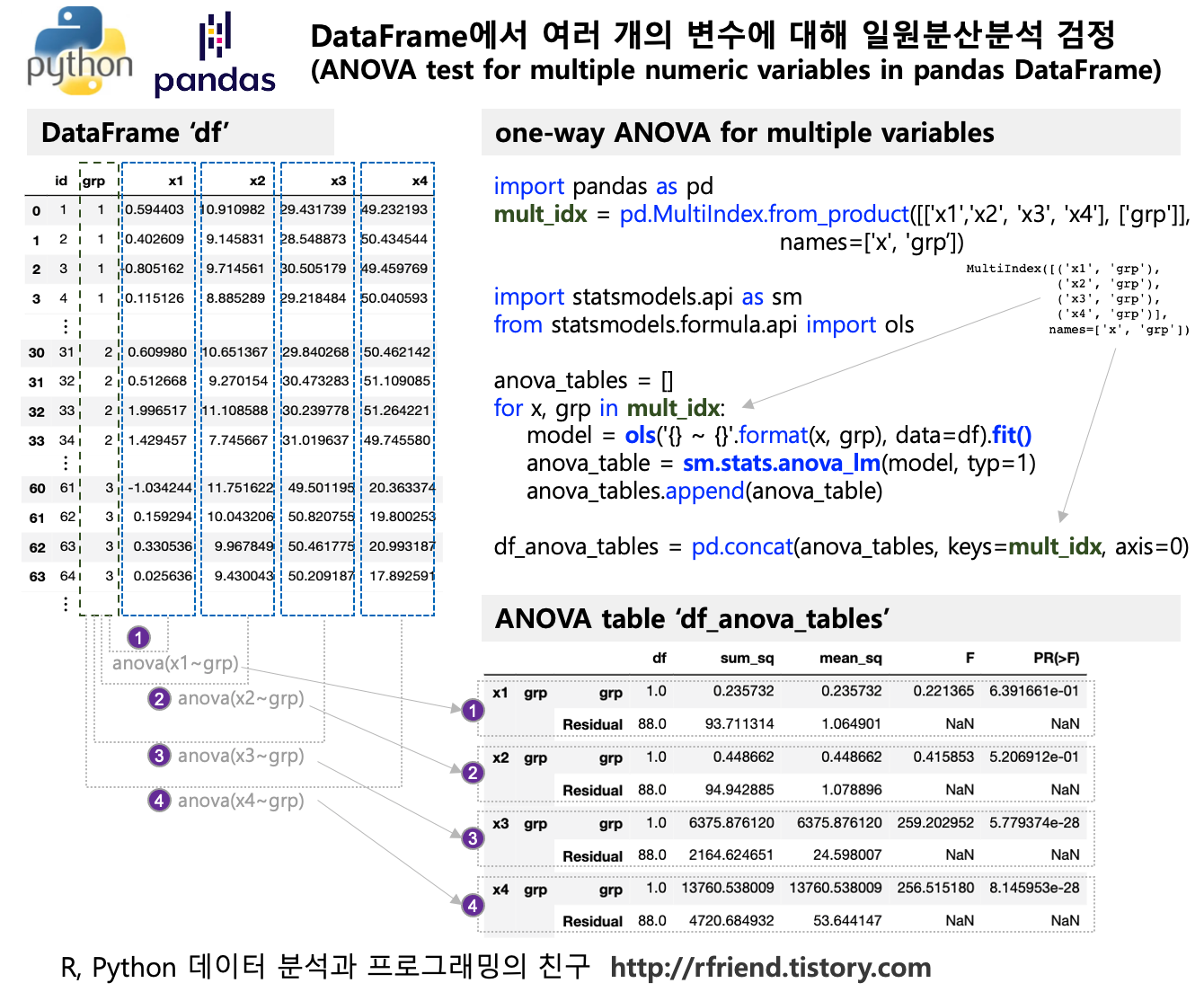
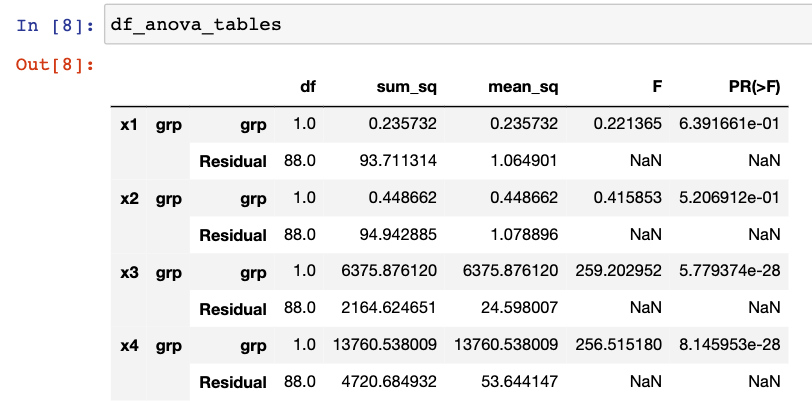
Greenplum and PostgreSQL Database 2021. 5. 9. 20:28지난번 포스팅에서는 Python의 statsmodels 모듈을 이용하여 여러개의 숫자형 변수에 대해 집단 간 평균의 차이가 있는지를 for loop 순환문을 사용하여 검정하는 방법(rfriend.tistory.com/639)을 소개하였습니다.
Python에서 for loop 문을 사용하면 순차적으로 처리 (sequential processing) 를 하게 되므로, 일원분산분석을 해야 하는 숫자형 변수의 개수가 많아질 수록 선형적으로 처리 시간이 증가하게 됩니다.
Greenplum에서 PL/Python (또는 PL/R) 을 사용하면 일원분산분석의 대상의 되는 숫자형 변수가 매우 많고 데이터 크기가 크더라도 분산병렬처리 (distributed parallel processing) 하여 ANOVA test 를 처리할 수 있으므로 신속하게 분석을 할 수 있는 장점이 있습니다.
더불어서, 데이터가 저장되어 있는 DB에서 데이터의 이동 없이(no data I/O, no data movement), In-DB 처리/분석이 되므로 work-flow 가 간소화되고 batch scheduling 하기에도 편리한 장점이 있습니다.
만약 데이터는 DB에 있고, 애플리케이션도 DB를 바라보고 있고, 분석은 Python 서버 (또는 R 서버)에서 하는 경우라면, 분석을 위해 DB에서 데이터를 samfile 로 떨구고, 이를 Python에서 pd.read_csv()로 읽어들여서 분석하고, 다시 결과를 text file로 떨구고, 이 text file을 ftp로 DB 서버로 이동하고, psql로 COPY 문으로 테이블에 insert 하는 workflow ... 관리 포인트가 많아서 정신 사납고 복잡하지요?!
자, 이제 Greenplum database에서 PL/Python으로 일원분산분석을 병렬처리해서 집단 간 여러개의 개별 변수별 평균 차이가 있는지 검정을 해보겠습니다.

(1) 여러 개의 변수를 가지는 샘플 데이터 만들기
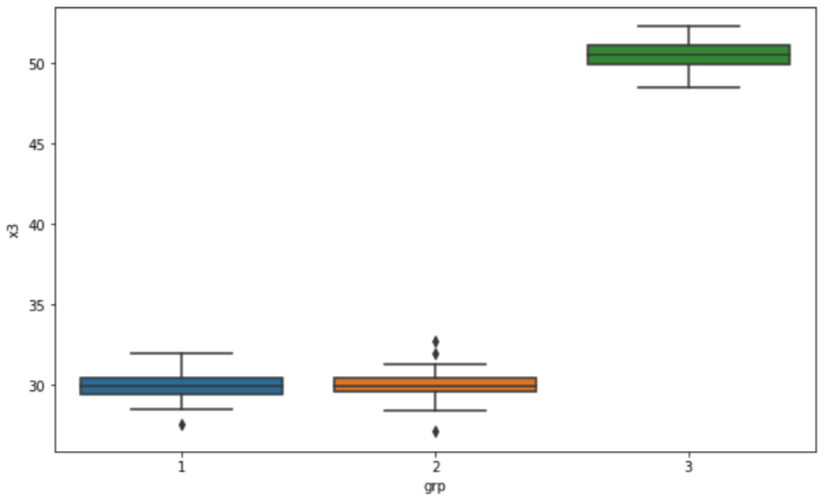
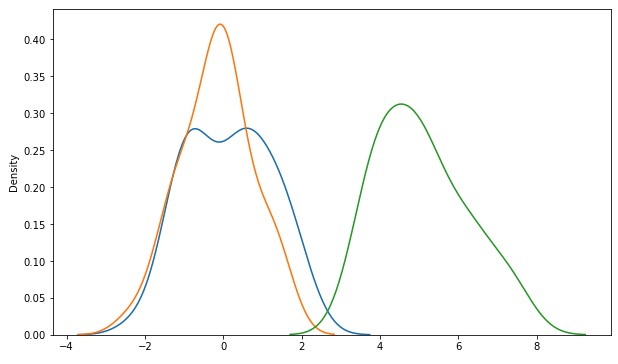
정규분포로 부터 난수를 발생시켜서 3개 그룹별로 각 30개 씩의 샘플 데이터를 생성하였습니다. 숫자형 변수로는 'x1', 'x2', 'x3', 'x4'의 네 개의 변수를 생성하였습니다. 이중에서 'x1', 'x2'는 3개 집단이 모두 동일한 평균과 분산을 가지는 정규분포로 부터 샘플을 추출하였고, 반면에 'x3', 'x4'는 3개 집단 중 2개는 동일한 평균과 분산의 정규분포로 부터 샘플을 추출하고 나머지 1개 집단은 다른 평균을 가지는 정규분포로 부터 샘플을 추출하였습니다. (뒤에 one-way ANOVA 검정을 해보면 'x3', 'x4'에 대한 집단 간 평균 차이가 있는 것으로 결과가 나오겠지요?!)
import numpy as np
import pandas as pd
# generate 90 IDs
id = np.arange(90) + 1
# Create 3 groups with 30 observations in each group.
from itertools import chain, repeat
grp = list(chain.from_iterable((repeat(number, 30) for number in [1, 2, 3])))
# generate random numbers per each groups from normal distribution
np.random.seed(1004)
# for 'x1' from group 1, 2 and 3
x1_g1 = np.random.normal(0, 1, 30)
x1_g2 = np.random.normal(0, 1, 30)
x1_g3 = np.random.normal(0, 1, 30)
# for 'x2' from group 1, 2 and 3
x2_g1 = np.random.normal(10, 1, 30)
x2_g2 = np.random.normal(10, 1, 30)
x2_g3 = np.random.normal(10, 1, 30)
# for 'x3' from group 1, 2 and 3
x3_g1 = np.random.normal(30, 1, 30)
x3_g2 = np.random.normal(30, 1, 30)
x3_g3 = np.random.normal(50, 1, 30)
# different mean
x4_g1 = np.random.normal(50, 1, 30)
x4_g2 = np.random.normal(50, 1, 30)
x4_g3 = np.random.normal(20, 1, 30)
# different mean # make a DataFrame with all together
df = pd.DataFrame({
'id': id, 'grp': grp,
'x1': np.concatenate([x1_g1, x1_g2, x1_g3]),
'x2': np.concatenate([x2_g1, x2_g2, x2_g3]),
'x3': np.concatenate([x3_g1, x3_g2, x3_g3]),
'x4': np.concatenate([x4_g1, x4_g2, x4_g3])})
df.head()
|
id |
grp |
x1 |
x2 |
x3 |
x4 |
|
1 |
1 |
0.594403 |
10.910982 |
29.431739 |
49.232193 |
|
2 |
1 |
0.402609 |
9.145831 |
28.548873 |
50.434544 |
|
3 |
1 |
-0.805162 |
9.714561 |
30.505179 |
49.459769 |
|
4 |
1 |
0.115126 |
8.885289 |
29.218484 |
50.040593 |
|
5 |
1 |
-0.753065 |
10.230208 |
30.072990 |
49.601211 |
위에서 만든 가상의 샘플 데이터를 Greenplum DB에 'sample_tbl' 이라는 이름의 테이블로 생성해보겠습니다. Python pandas의 to_sql() 메소드를 사용하면 pandas DataFrame을 쉽게 Greenplum DB (또는 PostgreSQL DB)에 uploading 할 수 있습니다.
# creating a table in Greenplum by importing pandas DataFrame
conn = "postgresql://gpadmin:changeme@localhost:5432/demo"
df.to_sql('sample_tbl',
conn,
schema = 'public',
if_exists = 'replace',
index = False)
Jupyter Notebook에서 Greenplum DB에 접속해서 SQL로 이후 작업을 진행하겠습니다.
(Jupyter Notebook에서 Greenplum DB access 하고 SQL query 실행하는 방법은 rfriend.tistory.com/572 참조하세요)
-- 여기서 부터는 Jupyter Notebook에서 실행한 것입니다. --
%load_ext sql
# postgresql://Username:Password@Host:Port/Database
%sql postgresql://gpadmin:changeme@localhost:5432/demo
[Out][
'Connected: gpadmin@demo'
위 (1) 에서 pandas 의 to_sql() 로 importing 한 sample_tbl 테이블에서 5개 행을 조회해보겠습니다.
%sql select * from sample_tbl order by id limit 5;
* postgresql://gpadmin:***@localhost:5432/demo
5 rows affected.
[Out]
id grp x1 x2 x3 x4
1 1 0.594403067344276 10.9109819091195 29.4317394311833 49.2321928075563
2 1 0.402608708677309 9.14583073327387 28.54887315985 50.4345438286737
3 1 -0.805162233589535 9.71456131309311 30.5051787625131 49.4597693977764
4 1 0.115125695763445 8.88528940547472 29.2184835450055 50.0405932387396
5 1 -0.753065219532709 10.230207786414 30.0729900069999 49.6012106088522
(2) 데이터 구조 변경: reshaping from wide to long
PL/Python에서 작업하기 쉽도록 테이블 구조를 wide format에서 long format 으로 변경하겠습니다. union all 로 해서 칼럼 갯수 만큼 위/아래로 append 해나가면 되는데요, DB 에서 이런 형식의 데이터를 관리하고 있다면 아마도 이미 long format 으로 관리하고 있을 가능성이 높습니다. (새로운 데이터가 수집되면 계속 insert into 하면서 행을 밑으로 계속 쌓아갈 것이므로...)
%%sql
-- reshaping a table from wide to long
drop table if exists sample_tbl_long;
create table sample_tbl_long as (
select id, grp, 'x1' as col, x1 as val from sample_tbl
union all
select id, grp, 'x2' as col, x2 as val from sample_tbl
union all
select id, grp, 'x3' as col, x3 as val from sample_tbl
union all
select id, grp, 'x4' as col, x4 as val from sample_tbl
) distributed randomly;
* postgresql://gpadmin:***@localhost:5432/demo
Done.
360 rows affected.
%sql select * from sample_tbl_long order by id, grp, col limit 8;
[Out]
* postgresql://gpadmin:***@localhost:5432/demo
8 rows affected.
id grp col val
1 1 x1 0.594403067344276
1 1 x2 10.9109819091195
1 1 x3 29.4317394311833
1 1 x4 49.2321928075563
2 1 x1 0.402608708677309
2 1 x2 9.14583073327387
2 1 x3 28.54887315985
2 1 x4 50.4345438286737
(3) 분석 결과 반환 composite type 정의
일원분산분석 결과를 반환받을 때 각 분석 대상 변수 별로 (a) F-통계량, (b) p-value 의 두 개 값을 float8 데이터 형태로 반환받는 composite type 을 미리 정의해놓겠습니다.
%%sql
-- Creating a coposite return type
drop type if exists plpy_anova_type cascade;
create type plpy_anova_type as (
f_stat float8
, p_val float8
);
* postgresql://gpadmin:***@localhost:5432/demo
Done.
Done.
(4) 일원분산분석(one-way ANOVA) PL/Python 사용자 정의함수 정의
집단('grp')과 측정값('val')을 input 으로 받고, statsmodels 모듈의 sm.stats.anova_lm() 메소드로 일원분산분석을 하여 결과 테이블에서 'F-통계량'과 'p-value'만 인덱싱해서 반환하는 PL/Python 사용자 정의 함수를 정의해보겠습니다.
%%sql
-- Creating the PL/Python UDF of ANOVA
drop function if exists plpy_anova_func(text[], float8[]);
create or replace function plpy_anova_func(grp text[], val float8[])
returns plpy_anova_type
as $$
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
df = pd.DataFrame({'grp': grp, 'val': val})
model = ols('val ~ grp', data=df).fit()
anova_result = sm.stats.anova_lm(model, typ=1)
return {'f_stat': anova_result.loc['grp', 'F'],
'p_val': anova_result.loc['grp', 'PR(>F)']}
$$ language 'plpythonu';
* postgresql://gpadmin:***@localhost:5432/demo
Done.
Done.
(5) 일원분산분석(one-way ANOVA) PL/Python 함수 분산병렬처리 실행
PL/Python 사용자 정의함수는 SQL query 문으로 실행합니다. 이때 PL/Python 이 'F-통계량'과 'p-value'를 반환하도록 UDF를 정의했으므로 아래처럼 (plpy_anova_func(grp_arr, val_arr)).* 처럼 ().* 으로 해서 모든 결과('F-통계량' & 'p-value')를 반환하도록 해줘야 합니다. (빼먹고 실수하기 쉬우므로 ().*를 빼먹지 않도록 주의가 필요합니다)
이렇게 하면 변수별로 segment nodes 에서 분산병렬로 각각 처리가 되므로, 변수가 수백~수천개가 있더라도 (segment nodes가 많이 있다는 가정하에) 분산병렬처리되어 신속하게 분석을 할 수 있습니다. 그리고 결과는 바로 Greenplum DB table에 적재가 되므로 이후의 application이나 API service에서 가져다 쓰기에도 무척 편리합니다.
%%sql
-- Executing the PL/Python UDF of ANOVA
drop table if exists plpy_anova_table;
create table plpy_anova_table as (
select
col
, (plpy_anova_func(grp_arr, val_arr)).*
from (
select
col
, array_agg(grp::text order by id) as grp_arr
, array_agg(val::float8 order by id) as val_arr
from sample_tbl_long
group by col
) a
) distributed randomly;
* postgresql://gpadmin:***@localhost:5432/demo
Done.
4 rows affected.
총 4개의 각 변수별 일원분산분석 결과를 조회해보면 아래와 같습니다.
%%sql
select * from plpy_anova_table order by col;
[Out]
* postgresql://gpadmin:***@localhost:5432/demo
4 rows affected.
col f_stat p_val
x1 0.773700830155438 0.46445029458511966
x2 0.20615939957339052 0.8140997216173114
x3 4520.512608893724 1.2379278415456727e-88
x4 9080.286130418674 1.015467388498996e-101
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)

'Greenplum and PostgreSQL Database' 카테고리의 다른 글
| [PostgreSQL, Greenplum] JOIN 으로 여러개의 테이블, 뷰 연결하기 (0) | 2021.05.30 |
|---|---|
| [Greenplum] DBeaver SQL 대문자 기본 설정, 테마 설정, 폰트 크기 설정 (0) | 2021.05.23 |
| [Greenplum DB] Greenplum 에서 PL/Python으로 Random Forest 분산병렬처리하여 Feature Importance 계산하기 (0) | 2021.04.18 |
| [Greenplum PostGIS] spatial_ref_sys 테이블에 신규 좌표계 등록하고 좌표 변환하기 (0) | 2021.03.14 |
| [Greenplum PostGIS] spatial_ref_sys 복제 테이블 생성하여 st_transform 함수 사용하기 (0) | 2021.03.14 |