[Python] 샘플 크기가 다른 2개 이상 그룹간 일원분산분석 (one-way ANOVA with different sized samples)
Python 분석과 프로그래밍/Python 통계분석 2021. 5. 7. 23:592개의 모집단에 대한 평균을 비교, 분석하는 통계적 기법으로 t-Test를 활용하였다면, 비교하고자 하는 집단이 2개 이상일 경우에는 분산분석 (ANOVA : Analysis Of Variance)를 이용합니다.
설명변수는 범주형 자료(categorical data)이어야 하며, 종속변수는 연속형 자료(continuous data) 일 때 2개 이상 집단 간 평균 비교분석에 분산분석(ANOVA) 을 사용하게 됩니다.
분산분석(ANOVA)은 기본적으로 분산의 개념을 이용하여 분석하는 방법으로서, 분산을 계산할 때처럼 편차의 각각의 제곱합을 해당 자유도로 나누어서 얻게 되는 값을 이용하여 수준평균들간의 차이가 존재하는 지를 판단하게 됩니다. 이론적인 부분에 대한 좀더 자세한 내용은 https://rfriend.tistory.com/131 를 참고하세요.
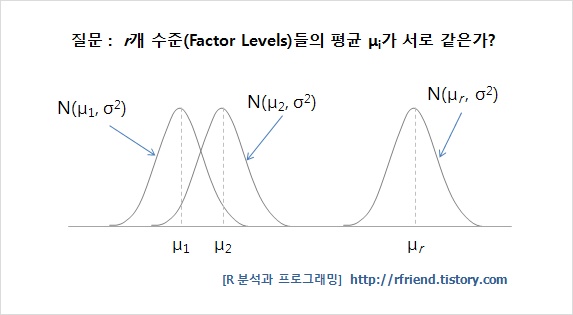
이번 포스팅에서는 Python의 scipy 모듈의 stats.f_oneway() 메소드를 사용하여 샘플의 크기가 서로 다른 3개 그룹 간 평균에 차이가 존재하는지 여부를 일원분산분석(one-way ANOVA)으로 분석하는 방법을 소개하겠습니다.
분산분석(Analysis Of Variance) 검정의 3가지 가정사항을 고려해서, 샘플 크기가 서로 다른 가상의 3개 그룹의 예제 데이터셋을 만들어보겠습니다.
[ 분산분석 검정의 가정사항 (assumptions of ANOVA test) ]
(1) 독립성: 각 샘플 데이터는 서로 독립이다.
(2) 정규성: 각 샘플 데이터는 정규분포를 따르는 모집단으로 부터 추출되었다.
(3) 등분산성: 그룹들의 모집단의 분산은 모두 동일하다.
먼저, 아래의 예제 샘플 데이터셋은 그룹1과 그룹2의 평균은 '0'으로 같고, 그룹3의 평균은 '5'로서 나머지 두 그룹과 다르게 난수를 발생시켜 가상으로 만든 것입니다.
# 3 groups of dataset with different sized samples
import numpy as np
import pandas as pd
np.random.seed(1004)
data1 = np.random.normal(0, 1, 50)
data2 = np.random.normal(0, 1, 40)
data3 = np.random.normal(5, 1, 30) # different mean
data123 = [data1, data2, data3]
print(data123)
[Out]
[array([ 0.59440307, 0.40260871, -0.80516223, 0.1151257 , -0.75306522,
-0.7841178 , 1.46157577, 1.57607553, -0.17131776, -0.91448182,
0.86013945, 0.35880192, 1.72965706, -0.49764822, 1.7618699 ,
0.16901308, -1.08523701, -0.01065175, 1.11579838, -1.26497153,
-1.02072516, -0.71342119, 0.57412224, -0.45455422, -1.15656742,
1.29721355, -1.3833716 , 0.3205909 , -0.59086187, -1.43420648,
0.60998011, 0.51266756, 1.9965168 , 1.42945668, 1.82880165,
-1.40997132, 0.49433367, 0.9482873 , -0.35274099, -0.15359935,
-1.18356064, -0.75440273, -0.85981073, 1.14256322, -2.21331694,
0.90651805, 2.23629 , 1.00743665, 1.30584548, 0.46669171]), array([-0.49206651, -0.08727244, -0.34919043, -1.11363541, -1.71982966,
-0.14033817, 0.90928317, -0.60012686, 1.03906073, -0.03332287,
-1.03424396, 0.15929405, 0.33053582, 0.02563551, -0.09213904,
-0.91851177, 0.3099129 , -1.24211638, -0.33113027, -1.64086666,
-0.27539834, -0.05489003, 1.50604364, -1.37756156, -1.25561652,
0.16120867, -0.42121705, 0.2341905 , -1.20155195, 1.48131392,
0.29105321, 0.4022031 , -0.41466037, 1.00502917, 1.45376705,
-0.07038153, 0.52897801, -2.37895295, -0.75054747, 1.10641762]), array([5.91098191, 4.14583073, 4.71456131, 3.88528941, 5.23020779,
5.12814125, 3.44610618, 5.36308351, 4.69463298, 7.49521024,
5.41246681, 3.8724271 , 4.60265531, 4.60082925, 4.9074518 ,
3.8141367 , 6.4457503 , 4.27553455, 3.63173152, 6.25540542,
3.77536981, 7.19435668, 6.25339789, 6.43469547, 4.27431061,
5.16694916, 7.21065725, 5.68274021, 4.81732021, 3.81650656])]
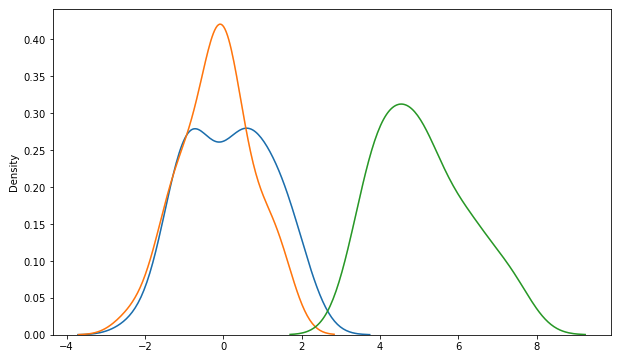
위의 3개 그룹의 커널밀도추정 그래프 (Kernel Density Estimates Plot)를 겹쳐서 그려보면, 아래와 같이 2개 집단은 서로 평균이 비슷하고 나머지 1개 집단은 평균이 확연히 다르다는 것을 직관적으로 알 수 있습니다.
# Kernel Density Estimate Plot
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = [10, 6]
sns.kdeplot(data1)
sns.kdeplot(data2)
sns.kdeplot(data3)
plt.show()
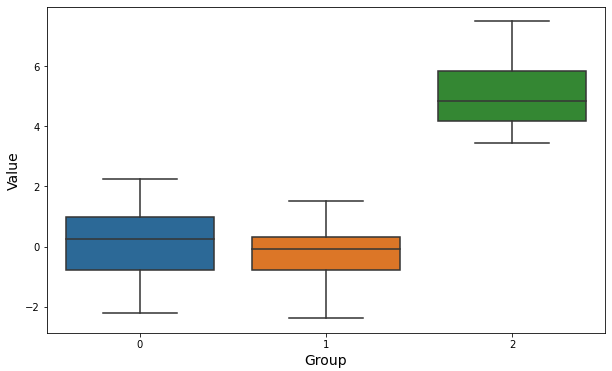
상자 그래프 (Box Plot) 으로 3개 집단 간 평균의 위치와 퍼짐 정도를 비교해보면, 역시 아래와 같이 그룹1과 그룹2는 서로 중심위치가 서로 비슷하고 그룹3만 중심위치가 확연히 다름을 알 수 있습니다.
# Boxplot
sns.boxplot(data=data123)
plt.xlabel("Group", fontsize=14)
plt.ylabel("Value", fontsize=14)
plt.show()
이제 scipy 모듈의 scipy.stats.f_oneway() 메소드를 사용해서 서로 다른 개수의 샘플을 가진 3개 집단에 대해 평균의 차이가 존재하는지 여부를 일원분산분석을 통해 검정을 해보겠습니다.
- 귀무가설(H0): 3 집단의 평균은 모두 같다. (mu1 = mu2 = m3)
- 대립가설(H1): 3 집단의 평균은 같지 않다.(적어도 1개 집단의 평균은 같지 않다) (Not H0)
F통계량은 매우 큰 값이고 p-value가 매우 작은 값이 나왔으므로 유의수준 5% 하에서 귀무가설을 기각하고 대립가설을 채택합니다. 즉, 3개 집단 간 평균의 차이가 존재한다고 평가할 수 있습니다.
# ANOVA with different sized samples using scipy
from scipy import stats
stats.f_oneway(data1, data2, data3)
[Out]
F_onewayResult(statistic=262.7129127080777, pvalue=5.385523527223916e-44)
F통계량과 p-value 를 각각 따로 따로 반환받을 수도 있습니다.
# returning f-statistic and p-value
f_val, p_val = stats.f_oneway(*data123)
print('f-statistic:', f_val)
print('p-vale:', p_val)
[Out]
f-statistic: 262.7129127080777
p-vale: 5.385523527223916e-44
scipy 모듈의 stats.f_oneway() 메소드를 사용할 때 만약 데이터에 결측값(NAN)이 포함되어 있으면 'NAN'을 반환합니다. 위에서 만들었던 'data1' numpy array 의 첫번째 값을 np.nan 으로 대체한 후에 scipy.stats.f_oneway() 로 일원분산분석 검정을 해보면 'NAN'(Not A Number)을 반환한 것을 볼 수 있습니다.
# if there is 'NAN', then returns 'NAN'
data1[0] = np.nan
print(data1)
[Out]
array([ nan, 0.40260871, -0.80516223, 0.1151257 , -0.75306522,
-0.7841178 , 1.46157577, 1.57607553, -0.17131776, -0.91448182,
0.86013945, 0.35880192, 1.72965706, -0.49764822, 1.7618699 ,
0.16901308, -1.08523701, -0.01065175, 1.11579838, -1.26497153,
-1.02072516, -0.71342119, 0.57412224, -0.45455422, -1.15656742,
1.29721355, -1.3833716 , 0.3205909 , -0.59086187, -1.43420648,
0.60998011, 0.51266756, 1.9965168 , 1.42945668, 1.82880165,
-1.40997132, 0.49433367, 0.9482873 , -0.35274099, -0.15359935,
-1.18356064, -0.75440273, -0.85981073, 1.14256322, -2.21331694,
0.90651805, 2.23629 , 1.00743665, 1.30584548, 0.46669171])
# returns 'nan'
stats.f_oneway(data1, data2, data3)
[Out]
F_onewayResult(statistic=nan, pvalue=nan)
샘플 데이터에 결측값이 포함되어 있는 경우, 결측값을 먼저 제거해주고 일원분산분석 검정을 실시해주시기 바랍니다.
# get rid of the missing values before applying ANOVA test
stats.f_oneway(data1[~np.isnan(data1)], data2, data3)
[Out]
F_onewayResult(statistic=260.766426640122, pvalue=1.1951277551195217e-43)
위의 일원분산분석(one-way ANOVA) 는 2개 이상의 그룹 간 평균의 차이가 존재하는지만을 검정할 뿐이며, 집단 간 평균의 차이가 존재한다는 대립가설을 채택하게 된 경우 어느 그룹 간 차이가 존재하는지는 사후검정 다중비교(post-hoc pair-wise multiple comparisons)를 통해서 알 수 있습니다. (rfriend.tistory.com/133)
pandas DataFrame 데이터셋에서 여러개의 숫자형 변수에 대해 for loop 순환문을 사용하여 집단 간 평균 차이 여부를 검정하는 방법은 rfriend.tistory.com/639 포스팅을 참고하세요.
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요.
[reference]
* scipy.stats.f_oneway : https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.f_oneway.html
scipy.stats.f_oneway — SciPy v1.6.3 Reference Guide
G.W. Heiman, “Understanding research methods and statistics: An integrated introduction for psychology”, Houghton, Mifflin and Company, 2001.
docs.scipy.org




