R (7) 벡터의 곱 - [2] 벡터곱 (cross product, vector product), 외적(outer product)
R 분석과 프로그래밍/R 선형대수 2015. 12. 20. 20:33지난번 포스팅에서 벡터의 곱 첫번째로 내적 (inner product, dot product, scalar product, projection product)에 대해서 알아보았습니다.
이번에는 벡터의 곱 두번째로 벡터곱(vector product, cross product)과 외적 (outer product)에 대해서 알아보도록 하겠습니다.
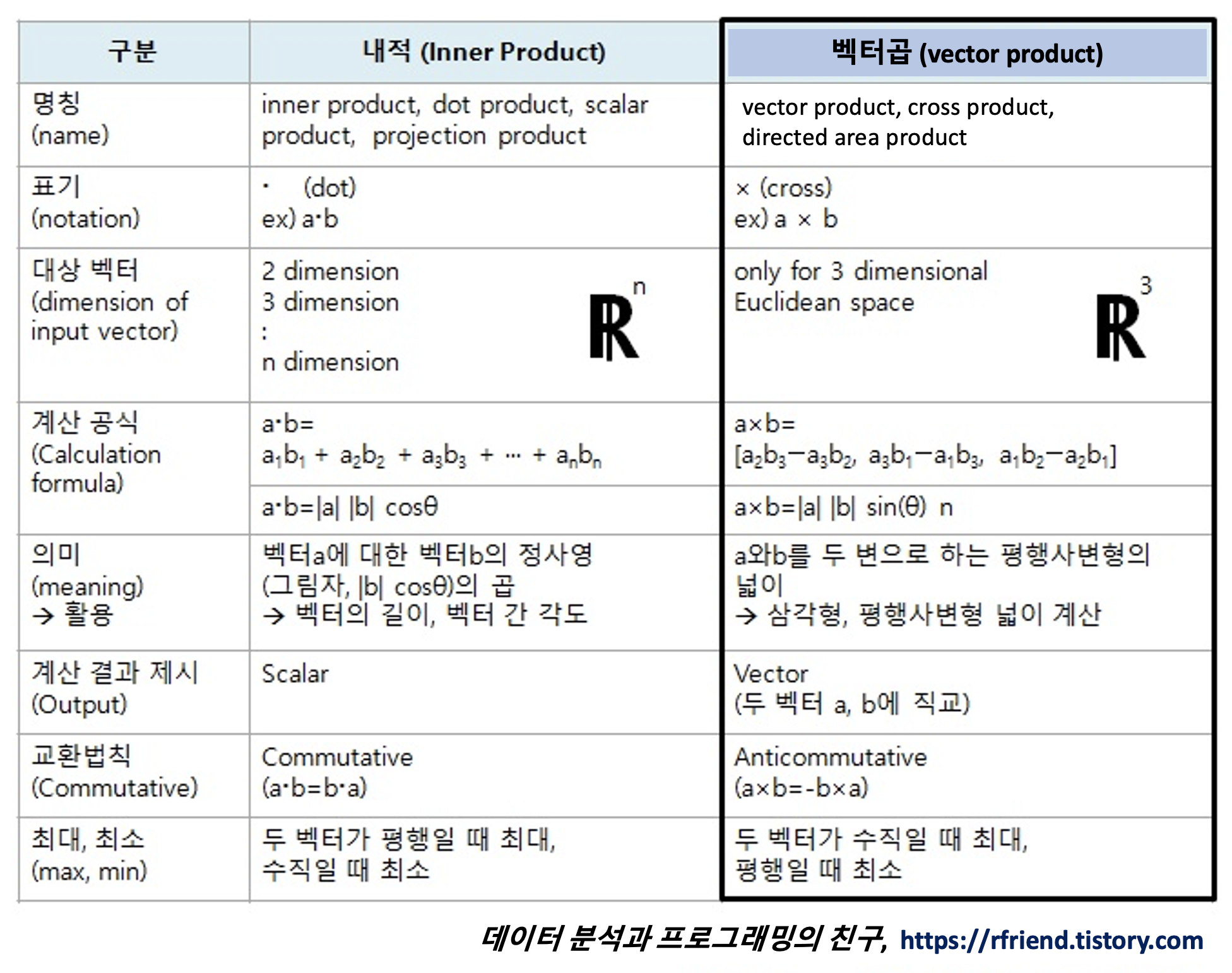
아래에는 내적과 벡터곱(vector product, cross product) 비교한 표입니다. 처음 보면 잘 이해가 안갈 수도 있는데요, 아래의 내용을 한번 쭉 보시고 마지막에 요약 정리할 때 참고하시면 도움이 될 듯 합니다. 큰 차이점 하나만 들자면, 내적(inner product)은 계산 결과로 스칼라(scalar)가 되지만, 벡터곱(vector product)은 계산 결과가 두 벡터 a와 b에 수직이 되는 벡터(vector)가 되고, 외적(outer product)은 행렬(matrix)가 된다는 점입니다.
[ 내적와 벡터곱 비교 ]
(comparison between inner product and vector product)
먼저 벡터곱(vector product, cross product, directed area product)에 대해서 차근차근 설명해 보겠습니다. 그리고 마지막에 외적(outer product) 계산법에 대해서 간략히 소개하겠습니다.
(1) 벡터곱의 표기 (notation and symbol of vector product)
두 벡터 a, b의 벡터곱은 a x b 라고 쓰고 "a cross b"라고 읽습니다. 벡터곱을 교차곱 (cross product)이라고도 부르는 이유가 여기에 있습니다. (참고로, 내적은 a·b 로 표기하고 a dot b 라고 읽으며 dot product 이라고도 함)
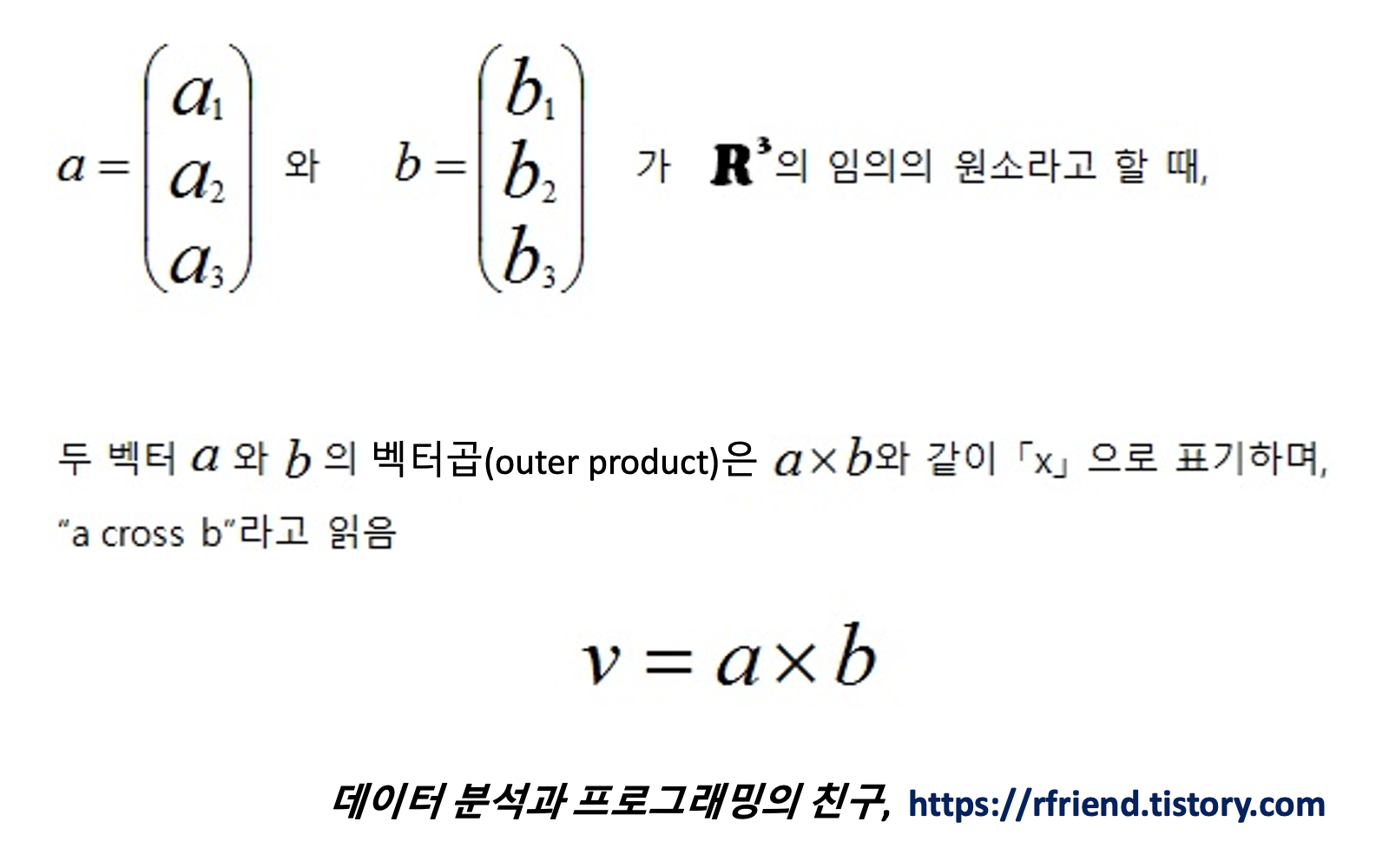
(2) 벡터곱의 정의 (definition of vector product)
두 벡터 a와 b에 모두 수직이 되는 벡터로서, v와 수직이 되는 두 벡터 a와 b는 공간 속의 평면 위에 있는 한 평행사변형의 두 변을 이루게 되며, 그 벡터의 길이(힘의 크기) |v|는 평행사변형의 면적과 같습니다.
(3) 벡터곱 계산을 쉽게 기억하는 방법 (easy way to memorize vector product calculation)
내적 대비 벡터곱 계산하는 방법이 많이 어려워보일 수 있는데요, 아래처럼 벡터 a와 b의 component를 두번씩 세로로 써 놓고 두번재째 행부터 순차적으로 대각선으로 곱하고 빼나가면 v1, v2, v3를 구할 수 있습니다.
(4) 벡터곱을 계산하는 R 사용자 정의 함수 (R user-defined function of vector product)
벡터곱(vector product, cross product)을 구하는 R 패키지, 함수가 분명 있을 것 같은데요, 제가 아직 못찾았습니다. 그래서 위에 소개한 공식대로 아래에 사용자 정의함수 프로그래밍 한거 소개합니다. 혹시라도 외적 구하는 R 패키지랑 함수 알고 계신분은 댓글로 공유해주시면 감사하겠습니다.
##---------
# (2) cross product of vector with 3 components : user defined function
# a * b = |a|*|b|*sin(theta)*n
cross_prod_fun_v3 <- function(a, b) {
if(length(a)!=3 | length(b) !=3) stop('number of vector component is not 3')
c_x <- a[2]*b[3] - a[3]*b[2]
c_y <- a[3]*b[1] - a[1]*b[3]
c_z <- a[1]*b[2] - a[2]*b[1]
cross_prd <- c(c_x, c_y, c_z)
return(cross_prd)
}
a <- c(2, 3, 4)
b <- c(5, 6, 7)
cross_prod_fun_v3(a=a, b=b)
[1] -3 6 -3
R의 %*%, crossprod() 함수는 외적이 아니라 내적을 계산한 결과를 내보내주므로 헷갈리지 않도록 해야겠습니다. 아래에 a=(2, 3, 4)와 b=(5, 6, 7) 벡터를 가지고 %*%, crossprod() 함수를 적용해봤더니 내적으로 계산해서 스칼라(scalar)가 나온것을 알 수 있습니다. (not vector, but scalar)
# cautions: crossprod() function of R produces dot product, not cross product
a <- c(2, 3, 4)
b <- c(5, 6, 7)
a %*% b
# dot product [,1] [1,] 56
crossprod(a, b)
# is the same with dot product [,1] [1,] 56
t(a) %*% b # is the same with dot product [,1] [1,] 56
(5) 오른손 법칙 (Right-handed triple), 오른손 직교좌표계 (Right-handed Cartesian coordinate system)
a와 b 두 벡터의 벡터곱이 벡터 a와 b에 직교 (right angle)하는 외적 v 벡터의 방향을 알 수 있는 방법으로 오른손 좌표계(Right-handed Cartesian coordinate system)을 사용합니다. 오른손의 엄지가 벡터 a, 오른손의 검지가 벡터 b, 그리고 오른손의 중지를 엄지와 검지랑은 수직이 되게 폈을 때가 외적 벡터 v 가 되겠습니다. 아래 그림을 참고하시지요.
오른손 법칙은 오른손 나사를 연상해도 되는데요, 벡터 a를 벡터 b의 방향으로 각도 θ만큼 회전시켰을 때 오른손 나사가 나아가는 방향과 같은 방향이 외적 v의 방향이 되겠습니다.
왼손 좌표계도 있는데요, 오른손 좌표계와는 중지의 방향이 반대가 된다는 점만 다릅니다.
(6) 길이와 싸인함수를 이용한 벡터곱 구하기 (vector product calculation with length and a sine function)
내적(inner product)을 계산할 때는 길이(length)와 코사인(cosine)을 사용해서 구하는데요, 벡터곱(vector product)은 벡터의 길이(length)와 싸인(sine) 함수를 이용해서 구할 수 있습니다. (증명은 생략합니다)
(7) 두 벡터로 이루어진 평행사변형의 넓이 계산 (calculation of the area of the parallelogram spanned by vector a and b)
두 벡터 a와 b의 벡터곱(vector product, cross product)은 두 벡터로 이루어진 평행사변형의 넓이와 같다고 하였습니다. 두 벡터 a와 b로 이루어진 평행사변형의 넓이를 구해보면 (6)번에서 제시한 두 벡터의 벡터곱 공식과 일치함을 알 수 있습니다. 두 벡터로 이루어진 평행사변형의 넓이를 구하고 싶으면 두 벡터의 벡터곱을 구하면 되겠습니다.
(8) 벡터곱의 성질 (properties of vector product)
벡터곱은 내적과 같은 성질도 있고 다른 성질도 있습니다. 임의의 실수와의 곱은 순서에 상관없이 모두 동일하다는 점과 분배법칙(distributive law)을 만족한다는 점은 내적과 벡터곱이 동일합니다.
반면에 내적은 교환법칙(commutative law)이 성립하지만, 벡터곱은 교환법칙이 성립하지 않는다(anti-commutative)는 점에서 차이가 있습니다. 그리고 벡터곱은 결합법칙도 일반적으로 성립하지 않는다(not associative)는 점 때문에 괄호를 생략하면 안됩니다. 내적은 결과가 scalar 이지만 벡터곱은 결과가 vector이므로 서로 다른 성질을 가지게 되는 것입니다.
(9) 벡터곱의 최대, 최소 (max, min of vector product)
(6)번에서 벡터곱을 구하는 공식이 v = |a|*|b|*sin(θ)n 이라고 하였는데요, 이 공식에서 두 벡터가 수직(angle between a and b = 90 degree)일 때 벡터곱이 최대(outer product is max), 두 벡터가 평행일 때(angle between a and b = 0 degree) 벡터곱이 최소(outer product is min)임을 유추할 수 있습니다.
(10) 외적 (outer product)
위에서 소개한 두 벡터의 벡터곱(vector product, cross product)의 결과는 벡터인 반면에, 두 벡터의 외적(outer product)의 결과는 행렬입니다. 두 벡터의 외적(outper product)은 아래와 같이 계산합니다.

많은 도움 되었기를 바랍니다.
행렬, 벡터 관련 포스팅은 아래 링크를 걸어놓았습니다.
☞ 행렬 기본 이해
☞ 행렬의 기본 연산 (+, -, *, /, ^, %*%, colMeans(), rowMeans(), colSums(), rowSums())
☞ 벡터의 기본 이해와 연산 (vector: addition, subtraction, multiplication by scalar)
☞ 벡터의 곱 (1) 내적 (inner product, dot product, scalar product, projection product)
이번 포스팅이 도움이 되었다면 아래의 공감 ♡ 꾸욱~ 눌러주세요. ^^























