[Python] 불균형 데이터에 대한 분류 모델 성과평가 지표 (performance metrics of binary classification for imbalanced data)
Python 분석과 프로그래밍/Python 기계학습 2023. 1. 29. 19:21지난번 포스팅에서는 불균형 데이터(imbalanced data)가 무엇이고, 분류 모델링 시 무엇이 문제인지에 대해서 알아보았습니다. --> https://rfriend.tistory.com/773
이번 포스팅부터는 불균형 데이터를 가지고 분류 모델링 시 대처방법에 대해서 몇 번에 나누어서 이론과 Python을 활용한 코드를 소개하겠습니다. 먼저 (3-1) 소수 클래스의 데이터 추가 수집과 (3-2) 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정 부터 시작해볼까요?
[ 불균형 데이터로 분류 모델링하는 방법 ]
1. 소수 클래스의 데이터 추가 수집 (Get more minority data)
2. 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정
(evaluation metrics for imbalanced classification)
3. 샘플링 방법 (Sampling methods)
3-1. Undersampling
: Random Sampling, Tomek Links
3-2. Oversampling
: Resampling, SMOTE, Borderline SMOTE, ADASYN
4. 비용 또는 가중치 조정 방법 (Cost, Weight)
5. Outlier detection 방법
: One-class SVM, Isolation Forest, DBSCAN clustering
6. 확률 튜닝 알고리즘 (Probability Tuning Algorithms)
1. 소수 클래스의 데이터 추가 수집 (Get more minority data)
만약 소수 집단의 데이터를 추가로 수집하거나 또는 생성할 수 있다면 두 집단의 구성비가 균형을 잡히도록 소수 집단의 개수를 늘리면 되겠습니다.
하지만, 데이터를 수집하는데는 시간과 비용 (time and cost) 이 소요된다는 점, 상황에 따라서는 소수 데이터의 추가 수집이 불가능하다는 점도 고려를 해야겠습니다. 이런 제약사항 때문에 알고리즘적으로 불균형 데이터 문제를 해결하는 방법을 알아둘 필요가 있습니다.
(다음번 포스팅부터 소개해요)
2. 불균형 데이터 분류 모델에 적합한 성능평가 지표 선정
(evaluation metrics for imbalanced classification)
균형 데이터 (balanced data)에 대한
- 분류 모델의 성능 평가 지표에 대한 이론은 https://rfriend.tistory.com/771 를 참고하구요,
- Python 을 이용한 분류 모델의 성능 평가 코드는 https://rfriend.tistory.com/772 를 참고하세요.
불균형 데이터 (imbalanced data)에 대한 분류 모델 평가 지표를 선정하는 데는
(a) 범주와 확률 중에서 무엇을 예측하는가?
(b) 두 범주가 동등하게 중요한가? 아니면 양성(Positive) 범주가 더 중요한가?
(c) False Negative, False Positive 가 동등하게 중요한가? 아니면 둘 중 하나가 더 중요한가?
의 질문에 대한 답변 별로 평가 지표가 달라집니다.
(아래의 ‘불균형 데이터에 대한 이진 분류 모델 평가 지표’ 참조)

(1) 범주(class labels)를 예측하고, 두 범주가 동등하게 중요하며, 다수 범주가 80~90% 이상으로서 불균형 데이터(imbalanced data)인 경우
--> Geometirc-Mean (or G-Mean)
G-Mean = sqrt(Sensitivity x Specificity)
기하평균 G-Mean 은 다수 집단 (Majority class)과 소수 집단 (Minority class) 간 모두의 분류 성능을 측정하는 지표입니다. 낮은 G-Mean 점수는 비록 음성 사례(negative cases)가 정확하게 분류가 되더라도 양성 사례(positive cases)의 분류는 저조한 성능을 보인다는 뜻입니다. G-Mean 지표는 음성 범주(negative class)의 과적합(over-fitting)을 피하고, 양성 범주(positive class)의 과소 적합(under-fitting)을 피하는데 중요하게 사용됩니다.
(2) 범주를 예측하고, 두 범주가 동등하게 중요하며, 다수 범주가 80~90% 미만인 균형 데이터(balanced data)는
--> 정확도(Accuracy) 평가지표를 사용하면 됩니다.
하지만, 불균형 데이터에 대해서 정확도 지표를 사용할 경우 다수 집단 만을 잘 분류하고 소수 집단에 대해서는 제대로 분류를 못해도 높은 정확도 점수가 나오는 문제가 있습니다.


(3) 범주 (class labels) 를 예측하고, 양성 범주 (Positive class)가 더 중요하며,
- False Negative, False Positve 가 동등하게 중요하면 (Sensitivity, Precision이 균형있으면 좋은 모델)
--> F1 Score
- False Negative 가 더 비용이 크면 (Sensitivity가 높으면 좋은 모델) --> F2 Score
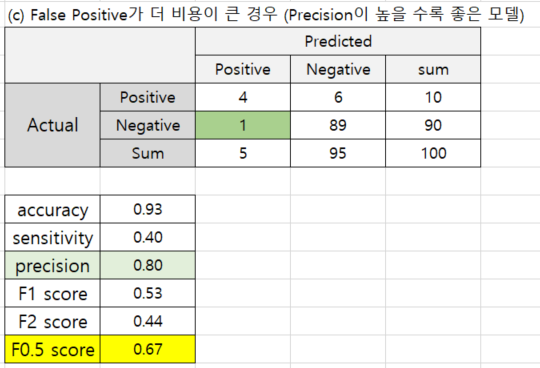
- False Positive 가 더 비용이 크면 (Precision이 높으면 좋은 모델) --> F0.5 Score
를 사용합니다.
F1 Score, F0.5 Score, F2 Score 는 높으면 높을수록 더 좋은 모델로 해석합니다.
참고로, 두 개의 범주가 바뀌어서 양성(Positive)이 음성(Negative)으로, 음성은 양성으로 바뀐 상태에서 혼돈 매트릭스를 만들어서 F2 Score를 계산하면 Inv F0.5 Score 가 됩니다. [2]

아래는 불균형 데이터에 대한 분류 모델의 혼돈 매트릭스를 3가지 시나리오 별로 가상으로 구성하여, 민감도(Sensitivity), 정밀도(Precision), F1 Score, F0.5 Score, F2 Score 를 계산해본 것입니다. 위 설명을 이해하는데 도움이 되기를 바랍니다.
(a) F1 Score는 정밀도(Precision)와 민감도(Sensitivity) 의 역수의 산술평균의 역수인 조화평균(Harmonic Mean)으로서, 정밀도와 민감도 간의 균형을 측정합니다. 만약 정밀도나 민감도가 0 이라면 F-Measure 는 0 이됩니다. F1 Score는 False Negative 와 False Positive가 동등하게 중요할 때의 모델 성능지표로 적합합니다. 민감도(Sensitivity)와 정밀도(Precision)이 균형있을 때 F1 Score가 높게 나옵니다.

(b) 불균형 데이터 (imbalanced data)인 경우에는 F0.5 Score 또는 F2 Score 를 사용하는데요, 비즈니스적으로 중요한 소수 범주(minority class)의 False Negative 가 더 비용(cost)이 크면(즉, Sensitivity가 높은 모델이 더 좋은 모델로서, Sensitiviey에 가중치를 더 줌) F2 Score 를 사용합니다. 예측된 양성이 비록 틀리는 비용을 감수하고서라도, 실제 양성(Positive)을 하나라도 더 분류해내고 싶을 때 F2 Score 지표를 사용합니다.

(c) 반대로, False Positive 가 비용이 더 크면(즉, (Precision이 높은 모델이 더 좋은 모델로서, Precision에 가중치를 더 줌) F0.5 Score를 모델 성능지표를 선택합니다. 실제 양성을 놓치는 비용을 감수하고서라도, 일단 모델이 양성으로 분류를 했으면 실제로도 양성이기를 바라는 경우에 F0.5 Score 지표를 사용합니다.
(4) 확률(Probability)을 예측하고, 확률 예측치의 정확도를 평가하고 싶을 때
--> Brier Score
Brier Score 는 확률 예측치의 정확도(accuracy of probability forecast)를 평가할 때 사용합니다. Brier Score 는 두개의 범주(bianry categories)를 가진 이진 분류(binary classification)의 예측 확률에만 사용할 수 모델 평가지표 입니다. [3]
Brier Score의 수식은 아래와 같이 모든 관측치에 대해서 예측확률과 실제 결과(발생하면 1, 아니면 0)와의 차이의 제곱합(Squared Summation)을 관측치의 개수로 나누어서 구한 ‘평균 제곱합 확률 오차(MSE, Mean Squared Error)’ 입니다.

Brier Score 는 작으면 작을 수록 이진 분류 모델의 확률 예측치가 정확하다는 뜻이며, 반대로 크면 클 수록 이진 분류 모델의 확률 예측치가 부정확하다고 해석합니다.
- 모든 확률 예측치에 대해서 완벽하게 모두 다 맞추면 Brier Score 는 0 이 됩니다. (최소값)
- 반대로, 모든 확률 예측치가 완벽하게 다 틀리면 Brier Score 는 1 이 됩니다. (최대값)
(5) 확률을 예측하고, 범주가 필요하며, 양성(Positive) 범주가 더 중요한 불균형 데이터의 경우
—> Precision-Recall Curve Plot, Precision-Recall AUC (Area Under the Curve)
Precision-Recall Curve 그림은 X축이 Recall, Y축이 Precision으로 해서, 두 범주를 분류하는 확률의 의사결정 기준점(Decision Treshold)을 0에서 1로 조금씩 변경해가면서 혼돈 매트릭스를 계산하고, 이어서 Precision과 Recall을 계산한 후에, 이 값들을 선으로 연결한 그래프입니다.
아래의 그래프처럼 Precision-Recall Curve 가 우측 상단으로 붙을 수록 불균형 데이터의 양성(Positive)을 더 잘 분류하는 모델이라고 평가할 수 있습니다. (Precision 과 Recall 은 Trade-off 관계에 있음).

ROC AUC 처럼, Precision-Recall Curve 의 아래 부분의 면적을 적분한 값이 PR AUC (Precision-Recall Area Under the Curve) 값이 됩니다. 하나의 score 로 계산이 되므로, 여러 모델을 수치적으로 비교할 수 있습니다. PR AUC가 크면 클 수록 소수의 양성 범주(minority Positive class) 를 잘 분류하는 모델이라고 평가할 수 있습니다.

[ Reference ]
(1) Tour of Evaluation Metrics for Imbalanced Classification
: https://machinelearningmastery.com/tour-of-evaluation-metrics-for-imbalanced-classification/
(2) "F-score" from Wikipedia: https://en.wikipedia.org/wiki/F-score
(3) Brier Score: https://www.statisticshowto.com/brier-score/




