[LangChain] pdf 파일과 대화기록을 참조하여 ChatGPT로 질의응답하기
Deep Learning (TF, Keras, PyTorch)/Natural Language Processing 2024. 1. 14. 21:43이번 포스팅에서는 여러개의 pdf 파일을 참조하여 ChatGPT로 질의응답하는 방법을 소개하겠습니다.
RAG (Retrieval0Augmented Generation) 방법을 사용한 답변 생성입니다.
1. pdf 파일을 로딩하고 임베딩으로 변환하여 Chroma Vector DB에 저장하고 인덱싱하기
2. 사용자 질문과 문서의 임베딩에 대해 Semantic Search하여 가장 유사한 문서 찾기
3. Semantic Search로 찾은 문서를 사용자 질문과 함께 ChatGPT에 보내서 답변 생성하기
4. 다른 pdf 파일을 로딩하고 임베딩으로 변환하여 Vector DB에 추가하기
5. 대화 기록에 대한 기억 (Chat History Memory)을 사용하여 ChatGPT 답변 생성하기
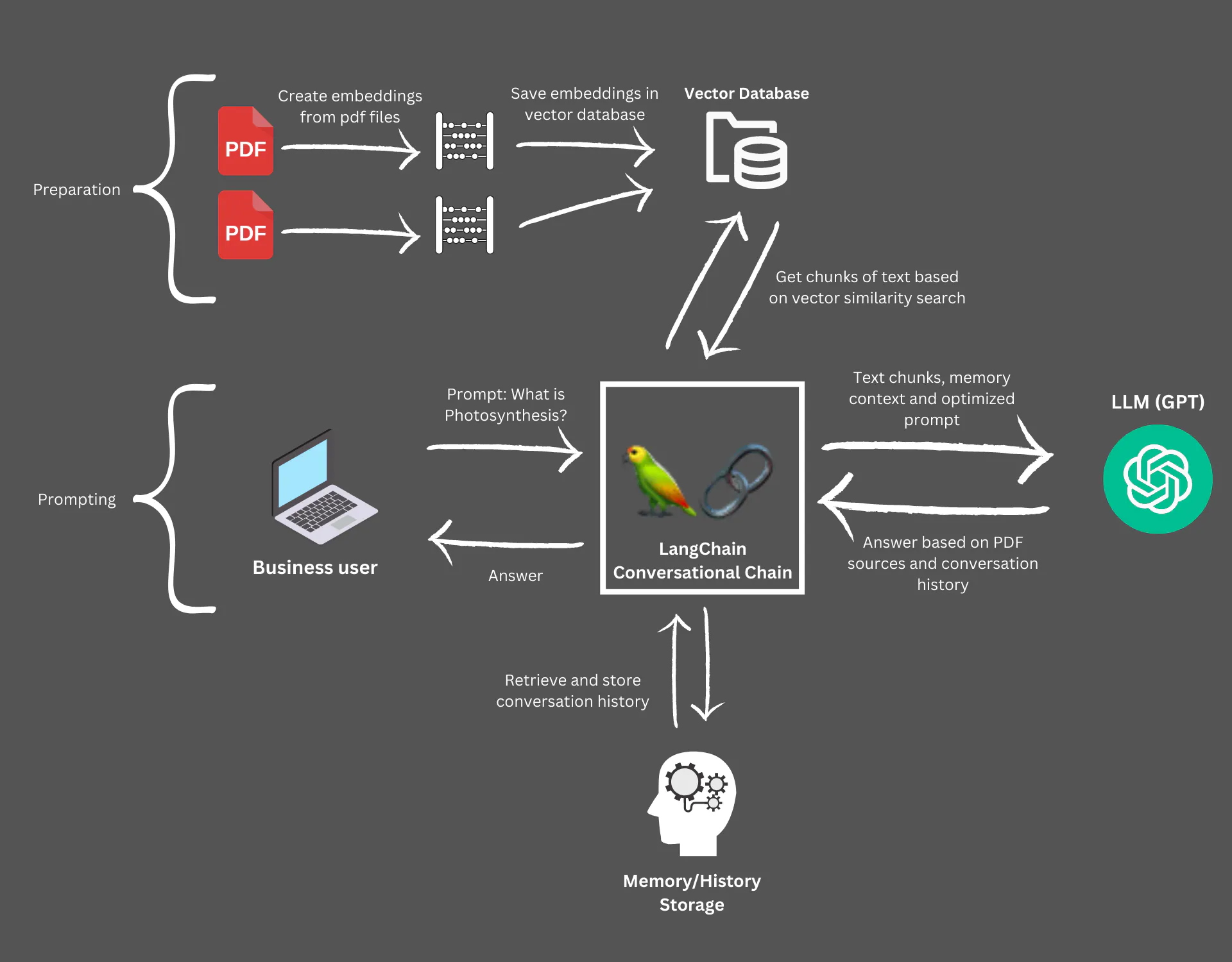
* source: https://www.datascienceengineer.com/blog/post-multiple-pdfs-with-gpt
먼저, 터미널에서 pip install 로 openai, langchain, pypdf, chroma 모듈을 설치합니다.
! pip install -q openai langchain pypdf chroma
1. pdf 파일을 로딩하고 임베딩으로 변환하여 Chroma Vector DB에 저장하고 인덱싱하기
아래에 필요한 모듈을 importing 합니다.
# Import the required modules
from langchain.document_loaders import PyPDFLoader
from langchain.vectorstores import Chroma
from langchain.chat_models import ChatOpenAI
from langchain.embeddings.openai import OpenAIEmbeddings
from langchain.text_splitter import RecursiveCharacterTextSplitter
from langchain.chains import RetrievalQA, ConversationalRetrievalChain
환경변수로 OpenAI의 ChatGPT를 사용하기 위한 API Key를 등록합니다.
# Set OpenAI API Key as an environment variable
import os
os.environ["OPENAI_API_KEY"]="sk-xxxx" # set with yours
LangChain 에서는 PDF (Portable Document Format) 파일을 로드할 수 있는 여러가지 방법을 제공합니다. 그중에서도 PyPDF 모듈을 이용해서 PDF 파일을 로드해보겠습니다.
# Load a PDF file, using the LangChain PyPDF loader
loader = PyPDFLoader("LangChain.pdf")
위에서 pdf 파일 문서를 로딩한 다음에는 RecursiveCharacterTextSplitter() 메소드를 사용해서 최대한 문장(sentence)를 유지한 상태의 작은 chunk 로 분할해줍니다. chuck_size, chunk_overlap 을 매개변수로 정의해줄 수 있습니다.
# Split the text in chunks, using LangChain Recursive Character Text Splitter
text_splitter = RecursiveCharacterTextSplitter(
chunk_size=1000,
chunk_overlap=200
)
pages = loader.load_and_split(text_splitter)
pdf 로드 후 분할을 하면 chunk 의 텍스트인 page_content, 그리고 소스 파일과 페이지 번호가 있는 metadata 에 각각 접근할 수 있습니다.
pages[0].page_content
# LangChain Introduction
# LangChain is a framework for developing applications powered by language models.
# ....
# LangServe : A library for deploying LangChain chains as a REST API.
# LangSmith : A developer platform that lets you debug, test, evaluate, and
pages[0].metadata
# {'source': 'LangChain.pdf', 'page': 0}
OpenAI의 Text Embedding 을 이용하여 chunk의 문서들을 임베딩 벡터로 변환하고, Chroma Vector DB에 저장하고 인덱싱합니다. 이때 메모리에만 남겨두는 것이 아니라 directory에 영구저장(persist)하여 추후 재사용할 수 있도록 합니다.
# Create a persistent, file-based vector store, using Chroma vector store.
directory = 'index_store'
vector_index = Chroma.from_documents(
pages, # Documents
OpenAIEmbeddings(), # Text embedding model
persist_directory=directory # persists the vectors to the file system
)
vector_index.persist()
Chroma Vector DB에 대한 자세한 내용은 https://www.trychroma.com/ 를 참고하세요.
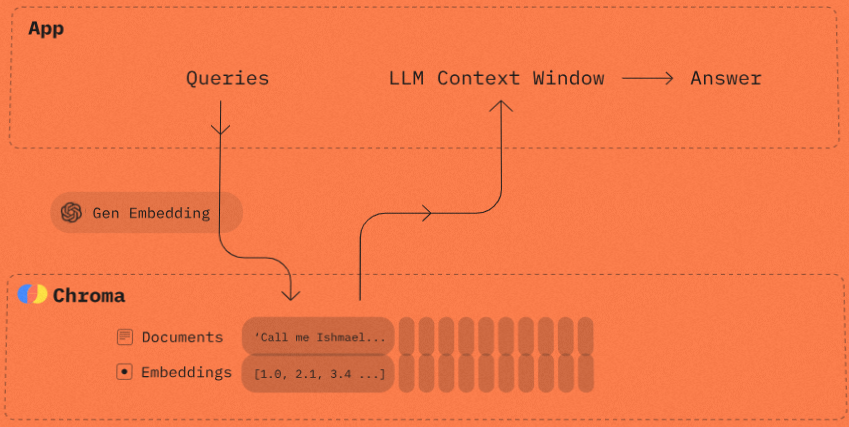
2. 사용자 질문과 문서의 임베딩에 대해 Semantic Search하여 가장 유사한 문서 찾기
위의 1번에서 pdf를 로딩하고 분할 후 임베딩 벡터로 변환하여 저장한 문서와 사용자 질문을 임베딩으로 변환한 벡터 간의 cosine similarity를 계산하여, 가장 유사한 k개의 문서를 검색 (Semantic Search)합니다.
LangChain 에서 제공하는 Vector store-backed retriever 에는 MMR (Maximum marginal relevance) retriever와 Similarity retriever 가 있습니다.
# Create the retriever and the query-interface.
retriever = vector_index.as_retriever(
search_type="similarity", # Cosine Similarity
search_kwargs={
"k": 3, # Select top k search results
}
)
위에서 정의한 Similarity retriever 를 사용하여 get_relevant_documents() 로 질문을 던져서 검색을 하여 질문과 가장 유사한 k개의 문서를 추출해보겠습니다.
retriever.get_relevant_documents("What is VectorStore for Retreival in LangChain?")
[Out]
[Document(page_content='allowing you to choose the one best suited for your needs. LangChain provides a \nstandard interface, allowing you to easily swap between models. \nVector stores \nWith the rise of embeddings, there has emerged a need for databases to support \nefficient storage and searching of these embeddings. LangChain provides \nintegrations with over 50 different vecto rstores, from open -source local ones to \ncloud -hosted proprietary ones, allowing you to choose the one best suited for your \nneeds. LangChain exposes a standard interface, allowing you to easily swap between \nvector stores. \nRetrievers \nOnce the data is in the database, you still need to retrieve it. LangChain supports \nmany different retrieval algorithms and is one of the places where we add the most \nvalue. LangChain supports b asic methods that are easy to get started - namely \nsimple semantic search. However, we have also added a collection of algorithms on \ntop of this to increase performance. These include:', metadata={'page': 2, 'source': 'LangChain.pdf'})]
3. Semantic Search로 찾은 문서를 사용자 질문과 함께 ChatGPT에 보내서 답변 생성하기
LangChain에 제공하는 Retrieval 기반 QA 클래스에는 RetrievalQA와 ConversationalRetrievalChain 의 두가지 종류가 있습니다.
- RetreivalQA: Retrieval 만을 사용하여 답변 생성
- ConversationalRetrievalChain: Chat History 기억과 Retrieval 을 같이 사용하여 답변 생성
먼저, RetrievalQA 클래스를 사용하여 ChatGPT에 Retrieval 만을 이용한 질의응답을 해보겠습니다. 아래 예에서는 temperature=0 으로 설정해서 보수적이고 일관적인 답변을 생성하도록 했으며, LLM 모델로는 ChatGPT-4 버전을 사용해보겠습니다. 그리고 return_source_documents=True 로 설정하여 답변 생성에 참고한 소스 문서를 같이 반환하도록 하여 나중에 사용자가 확인할 수 있도록 하였습니다.
# Create the chain for allowing us to chat with the document.
qa_chain = RetrievalQA.from_chain_type(
llm=ChatOpenAI(temperature=0, model="gpt-4"),
chain_type="stuff",
retriever=retriever,
return_source_documents=True # source document which were used as source files
)
위에서 작성한 qa_chain 에 대해 invoke() 메소드를 사용해서 사용자 질문을 던지면, ChatGPT는 답변 결과(result)와 답변을 생성할 때 참고했던 소스 문서(source_documents)를 반환합니다.
# Query the pdf file
qa_chain.invoke("What is VectorStore for Retrieval in LangChain")
# {'query': 'What is VectorStore for Retrieval in LangChain',
# 'result': 'VectorStore for Retrieval in LangChain refers to the feature that allows LangChain to integrate with over 50 different vector stores. These vector stores can be open-source local ones or cloud-hosted proprietary ones. The VectorStore feature in LangChain allows users to efficiently store and search embeddings, which are representations of textual data in a numerical format. This feature provides flexibility for users to choose the vector store that best suits their needs. LangChain also provides a standard interface that allows users to easily swap between different vector stores.',
# 'source_documents': [Document(page_content='allowing you to choose the one best suited for your needs. LangChain provides a \nstandard interface, allowing you to easily swap between models. \nVector stores \nWith the rise of embeddings, there has emerged a need for databases to support \nefficient storage and searching of these embeddings. LangChain provides \nintegrations with over 50 different vecto rstores, from open -source local ones to \ncloud -hosted proprietary ones, allowing you to choose the one best suited for your \nneeds. LangChain exposes a standard interface, allowing you to easily swap between \nvector stores. \nRetrievers \nOnce the data is in the database, you still need to retrieve it. LangChain supports \nmany different retrieval algorithms and is one of the places where we add the most \nvalue. LangChain supports b asic methods that are easy to get started - namely \nsimple semantic search. However, we have also added a collection of algorithms on \ntop of this to increase performance. These include:', metadata={'page': 2, 'source': 'LangChain.pdf'}),
# Document(page_content='allowing you to choose the one best suited for your needs. LangChain provides a \nstandard interface, allowing you to easily swap between models. \nVector stores \nWith the rise of embeddings, there has emerged a need for databases to support \nefficient storage and searching of these embeddings. LangChain provides \nintegrations with over 50 different vecto rstores, from open -source local ones to \ncloud -hosted proprietary ones, allowing you to choose the one best suited for your \nneeds. LangChain exposes a standard interface, allowing you to easily swap between \nvector stores. \nRetrievers \nOnce the data is in the database, you still need to retrieve it. LangChain supports \nmany different retrieval algorithms and is one of the places where we add the most \nvalue. LangChain supports b asic methods that are easy to get started - namely \nsimple semantic search. However, we have also added a collection of algorithms on \ntop of this to increase performance. These include:', metadata={'page': 2, 'source': 'LangChain.pdf'}),
# Document(page_content='\uf0b7 And more! \nIndexing \nThe LangChain Indexing API syncs your data from any source into a vector store, \nhelping you: \n\uf0b7 Avoid writing duplicated content into the vector store \n\uf0b7 Avoid re -writing unchanged content \n\uf0b7 Avoid re -computing embeddings over unchanged content \nAll of which should save you time and money, as well as improve your vector search \nresults.', metadata={'page': 2, 'source': 'LangChain.pdf'})]}
4. 다른 pdf 파일을 로딩하고 임베딩으로 변환하여 Vector DB에 추가하기
위의 1~3에서 사용했던 pdf 문서와는 다른 pdf 문서를 추가로 로딩, 분할, 임베딩 변환, Vector DB에 저장, 인덱싱하여, 여러개의 pdf 문서들을 참고하여 질의응답을 할 수 있습니다.
vector_index.add_documents() 로 기존의 Chroma Vector DB에 임베딩 변환, 저장해주고, persist() 로 파일 기반의 Vector Store에 영구저장할 수 있습니다.
# Adding additional documents to vector store
# Load a PDF file, using the LangChain PyPDF loader
loader = PyPDFLoader("Chain-of-Thought-prompting.pdf")
# Split the text in chunks, using LangChain Recursive Character Text Splitter
pages_new = loader.load_and_split(text_splitter)
# Add additional documents to vector store
_ = vector_index.add_documents(pages_new)
# Create a persistent, file-based vector store, using Chroma vector store.
vector_index.persist()
그러면 qa_chain.invoke() 로 기존 chain에 대해 사용자 질의를 했을 때 위의 4번에서 새로 추가한 pdf 문서의 내용까지 검색, 참조하여 답변을 생성해줍니다. (아래 예제에서는 두번째로 추가한 Chain-of-Thought-prompting.pdf 파일을 참조해서 적절한 답변을 생성했음)
# Query the pdf file
qa_chain.invoke("What is Chain-of-Thought Prompting?")
# {'query': 'What is Chain-of-Thought Prompting?',
# 'result': 'Chain-of-Thought Prompting is a method used to improve the reasoning abilities of large language models. It involves generating a series of intermediate reasoning steps, called a chain of thought, and using these demonstrations as prompts for the language model. The idea is that by providing examples of how to reason through a problem, the language model can better perform complex reasoning tasks. This approach has shown promising results in improving performance on arithmetic, commonsense, and symbolic reasoning tasks.',
# 'source_documents': [Document(page_content='C Extended Related Work\nChain-of-thought prompting is a general approach that is inspired by several prior directions: prompt-\ning, natural language explanations, program synthesis/execution, numeric and logical reasoning, and\nintermediate language steps.\nC.1 Prompting\nThe recent success of large-scale language models has led to growing interest in improving their\ncapability to perform tasks via prompting (Brown et al. (2020), and see Liu et al. (2021) for a\nsurvey). This paper falls in the category of general prompting approaches, whereby input prompts are\noptimized to allow a single large language model to better perform a variety of tasks (Li and Liang,\n2021; Lester et al., 2021; Reif et al., 2022, inter alia ).\nOne recent line of work aims to improve the ability of language models to perform a task by providing\ninstructions that describe the task (Raffel et al., 2020; Wei et al., 2022a; Ouyang et al., 2022; Sanh', metadata={'page': 23, 'source': 'Chain-of-Thought-prompting.pdf'}),
# Document(page_content='Chain-of-Thought Prompting Elicits Reasoning\nin Large Language Models\nJason Wei Xuezhi Wang Dale Schuurmans Maarten Bosma\nBrian Ichter Fei Xia Ed H. Chi Quoc V . Le Denny Zhou\nGoogle Research, Brain Team\n{jasonwei,dennyzhou}@google.com\nAbstract\nWe explore how generating a chain of thought —a series of intermediate reasoning\nsteps—significantly improves the ability of large language models to perform\ncomplex reasoning. In particular, we show how such reasoning abilities emerge\nnaturally in sufficiently large language models via a simple method called chain-of-\nthought prompting , where a few chain of thought demonstrations are provided as\nexemplars in prompting.\nExperiments on three large language models show that chain-of-thought prompting\nimproves performance on a range of arithmetic, commonsense, and symbolic\nreasoning tasks. The empirical gains can be striking. For instance, prompting a\nPaLM 540B with just eight chain-of-thought exemplars achieves state-of-the-art', metadata={'page': 0, 'source': 'Chain-of-Thought-prompting.pdf'}),
# Document(page_content='2021). In this paper, we combine the strengths of these two ideas in a way that avoids their limitations.\nSpecifically, we explore the ability of language models to perform few-shot prompting for reasoning\ntasks, given a prompt that consists of triples: ⟨input, chain of thought , output⟩. Achain of thought is\na series of intermediate natural language reasoning steps that lead to the final output, and we refer to\nthis approach as chain-of-thought prompting . An example prompt is shown in Figure 1.\nWe present empirical evaluations on arithmetic, commonsense, and symbolic reasoning benchmarks,\nshowing that chain-of-thought prompting outperforms standard prompting, sometimes to a striking\ndegree. Figure 2 illustrates one such result—on the GSM8K benchmark of math word problems\n(Cobbe et al., 2021), chain-of-thought prompting with PaLM 540B outperforms standard prompting\nby a large margin and achieves new state-of-the-art performance. A prompting only approach is', metadata={'page': 1, 'source': 'Chain-of-Thought-prompting.pdf'})]}
5. 대화 기록에 대한 기억 (Chat History Memory)을 사용하여 ChatGPT 답변 생성하기
마지막으로 ConversationalRetrievalChain 클래스를 사용해서 '대화 내역에 대한 기억 (Chat History Memory) + Retrieval' 을 동시에 고려하여 사용자 질의에 대한 답변을 생성해보겠습니다.
## Adding memory to conversations
# Instead of the RetrievalQA chain, we'll use the ConversationalRetrievalChain.
# ConversationalRetrievalChain allows to seamlessly add historical context or memory to chain.
conv_chain = ConversationalRetrievalChain.from_llm(
ChatOpenAI(temperature=0, model="gpt-4"),
retriever=retriever,
)
chat_history 리스트를 만들어주고, conv_chain.invoke() 로 질의응답을 할 때마다 {"chat_history": chat_history} 에 질문과 답변의 대화 내역을 차곡차곡 저장(chat_history.append((query, result["result"])))해줍니다.
# Initialize our chat history.
chat_history = []
query = "What is LangChain?"
result = conv_chain.invoke({"question": query, "chat_history": chat_history})
print(result["answer"])
# 'LangChain is a framework for developing applications powered by language models.
# It enables applications to be context-aware and reason based on the provided context.
# The framework consists of several parts including LangChain Libraries, LangChain Templates,
# LangServe, and LangSmith. The libraries contain interfaces and integrations
# for various components, a basic runtime for combining these components into chains
# and agents, and off-the-shelf implementations of chains and agents.
# The templates are a collection of easily deployable reference architectures
# for a wide variety of tasks. LangServe is a library for deploying LangChain chains as a REST API,
# and LangSmith is a developer platform for debugging, testing, and evaluating.'
# Add previous conversation to chat history
chat_history.append((query, result["answer"]))
이러면 질의응답 기억을 참고하여 새로운 답변을 생성할 수 있습니다. 아래 예에서는 위의 답변을 줄여서 요약하라고 지시했습니다.
# Query to shorten the last sentence
query = "Can you shorten the answer above?"
result = conv_chain.invoke({"question": query, "chat_history": chat_history})
print(result["answer"])
# 'LangChain is a framework used for developing applications that are powered by language models.
# It allows these applications to be context-aware and capable of reasoning based on provided context.
# The framework includes Python and JavaScript libraries, deployable templates for various tasks,
# a library for deploying as a REST API, and a developer platform for debugging, testing, and evaluation.'
질문과 답변을 나중에 참조할 수 있도록 chat_history.append((query, result["answer"])) 로 기억으로 저장해둡니다.
chat_history.append((query, result["answer"]))
chat_history
# [('What is LangChain?',
# 'LangChain is a framework for developing applications powered by language models. It enables applications to be context-aware and reason based on the provided context. The framework consists of several parts including LangChain Libraries, LangChain Templates, LangServe, and LangSmith. The libraries contain interfaces and integrations for various components, a basic runtime for combining these components into chains and agents, and off-the-shelf implementations of chains and agents. The templates are a collection of easily deployable reference architectures for a wide variety of tasks. LangServe is a library for deploying LangChain chains as a REST API, and LangSmith is a developer platform for debugging, testing, and evaluating.'),
# ('Can you shorten the answer above?',
# 'LangChain is a framework used for developing applications that are powered by language models. It allows these applications to be context-aware and capable of reasoning based on provided context. The framework includes Python and JavaScript libraries, deployable templates for various tasks, a library for deploying as a REST API, and a developer platform for debugging, testing, and evaluation.')]
[ Reference ]
* How to use LangChain and GPT to ask questions on multiple pdf documents:
https://www.datascienceengineer.com/blog/post-multiple-pdfs-with-gpt
* LangChain - Document Loaders - PDF:
https://python.langchain.com/docs/modules/data_connection/document_loaders/pdf
* OpenAI Text Embedding:
https://platform.openai.com/docs/guides/embeddings
* Chroma - AI-native open-source embedding database:
https://www.trychroma.com/
* Vector store-backed retriever:
https://python.langchain.com/docs/modules/data_connection/retrievers/vectorstore
* 위 실습에 사용한 pdf 파일: LangChain.pdf, Chain-of-Thought-prompting.pdf
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요.




