[Python] 지수평활법 모형 훈련 및 예측, 모델평가 (Exponential Smoothing in Python)
Python 분석과 프로그래밍/Python 통계분석 2021. 7. 29. 19:49지난번 포스팅에서는 시계열 패턴 별 지수평활법 모델을 설정하는 방법 (https://rfriend.tistory.com/511), 그리고 시계열 데이터 예측 모델의 성능, 모델 적합도 (goodness-of-fit of time series model)를 평가하는 지표 (https://rfriend.tistory.com/667) 에 대해서 소개하였습니다.
이번 포스팅에서는 간단한 시계열 예제 데이터에 대해 앞서 소개한 이론들을 Python 코드로 실습하여
(1) 지수평활법(Exponential Smoothing) 기법으로 시계열 예측 모델을 만들고,
(2) 모델 적합도를 평가하는 여러 지표들로 성능을 평가해서 최적의 모델을 선택
해보겠습니다.
예제로 사용할 시계열 데이터는 1991년 7월부터 2008년 6월까지 월 단위(monthly)로 집계된 약 판매량 시계열 데이터셋 (drug sales time series dataset) 입니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
## getting drug sales dataset
file_path = 'https://raw.githubusercontent.com/selva86/datasets/master/a10.csv'
df = pd.read_csv(file_path,
parse_dates=['date'],
index_col='date')
df.head(12)
# [Out]
# value
# date
# 1991-07-01 3.526591
# 1991-08-01 3.180891
# 1991-09-01 3.252221
# 1991-10-01 3.611003
# 1991-11-01 3.565869
# 1991-12-01 4.306371
# 1992-01-01 5.088335
# 1992-02-01 2.814520
# 1992-03-01 2.985811
# 1992-04-01 3.204780
# 1992-05-01 3.127578
# 1992-06-01 3.270523
## time series plot
df.plot(figsize=[12, 8])
plt.title('Drug Sales', fontsize=14)
plt.show()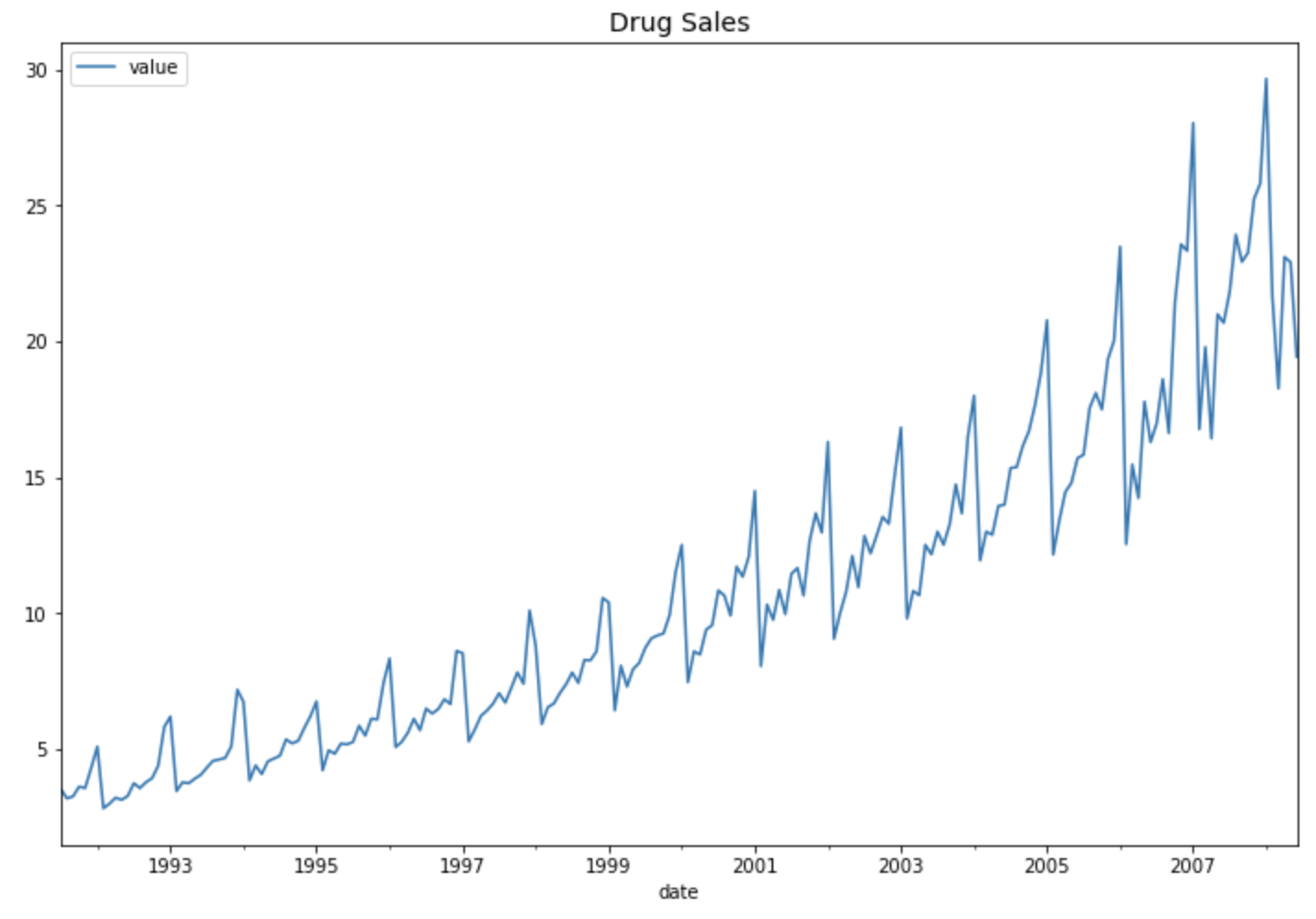
위의 약 판매량 시도표 (time series plot of drug sales) 를 보면 세 가지를 알 수 있습니다.
(a) 선형 추세가 존재합니다. (linear or quadratic trend)
(b) 1년 단위의 계절성이 존재합니다. (seasonality of a year, ie. 12 months)
(c) 분산이 시간의 흐름에 따라 점점 커지고 있습니다. (increasing variation)
우리가 관찰한 이들 세가지의 시계열 데이터의 패턴으로 부터 "Multiplicative Winters' method with Linear / Quadratic Trend" 모델이 적합할 것이라고 판단해볼 수 있습니다.
* 참조: 시계열 패턴 별 지수평활법 모델을 설정하는 방법 (https://rfriend.tistory.com/511)
그럼, 실제로 다양한 지수평활법으로 위의 약 판매량 시계열 데이터에 대한 예측 모델을 만들어 예측을 해보고, 다양한 평가지표로 모델 간 비교를 해봐서 가장 우수한 모델이 무엇인지, 과연 앞서 말한 "Multiplicative Winters' method with Linear Trend" 모델이 가장 우수할 것인지 확인해보겠습니다. 보는게 믿는거 아니겠습니까!
이제 월 단위로 시간 순서대로 정렬된 시계열 데이터를 제일 뒤 (최근)의 12개월치는 시계열 예측 모델의 성능을 평가할 때 사용할 test set으로 따로 떼어놓고, 나머지 데이터는 시계열 예측모형 훈련에 사용할 training set 으로 분할 (splitting between the training and the test set)을 해보겠습니다.
## split between the training and the test data sets.
## The last 12 periods form the test data
df_train = df.iloc[:-12]
df_test = df.iloc[-12:]
(1) 지수평활법 기법으로 시계열 예측모형 적합하기
(training the exponential smoothing models in Python)
Python의 statsmodels 라이브러리는 시계열 데이터 분석을 위한 API를 제공합니다. 아래의 코드는 순서대로
(a) Simple Exponential Smoothing
-- 추세 요소의 유형 (type of trend components)에 따라서
(b) Holt's (trend=None)
(c) Exponential trend (exponential=True)
(d) Additive damped trend (damped_trend=True)
(e) Multiplicative damped trend (exponential=True, damped_trend=True)
로 구분할 수 있습니다.
## exponential smoothing in Python
from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt
# Simple Exponential Smoothing
fit1 = SimpleExpSmoothing(df_train,
initialization_method="estimated").fit()
# Trend
fit2 = Holt(df_train,
initialization_method="estimated").fit()
# Exponential trend
fit3 = Holt(df_train,
exponential=True,
initialization_method="estimated").fit()
# Additive damped trend
fit4 = Holt(df_train,
damped_trend=True,
initialization_method="estimated").fit()
# Multiplicative damped trend
fit5 = Holt(df_train,
exponential=True,
damped_trend=True,
initialization_method="estimated").fit()
statsmodels.tsa.api 메소드를 사용해서 적합한 시계열 데이터 예측 모델에 대해서는 model_object.summary() 메소드를 사용해서 적합 결과를 조회할 수 있습니다. 그리고 model_object.params['parameter_name'] 의 방식으로 지수평활법 시계열 적합 모델의 속성값(attributes of the fitted exponential smoothing results)에 대해서 조회할 수 있습니다.
## accessing the results of SimpleExpSmoothing Model
print(fit1.summary())
# SimpleExpSmoothing Model Results
# ==============================================================================
# Dep. Variable: value No. Observations: 192
# Model: SimpleExpSmoothing SSE 692.196
# Optimized: True AIC 250.216
# Trend: None BIC 256.731
# Seasonal: None AICC 250.430
# Seasonal Periods: None Date: Thu, 29 Jul 2021
# Box-Cox: False Time: 19:26:46
# Box-Cox Coeff.: None
# ==============================================================================
# coeff code optimized
# ------------------------------------------------------------------------------
# smoothing_level 0.3062819 alpha True
# initial_level 3.4872869 l.0 True
# ------------------------------------------------------------------------------
## getting all results by models
params = ['smoothing_level', 'smoothing_trend', 'damping_trend', 'initial_level', 'initial_trend']
results=pd.DataFrame(index=[r"$\alpha$",r"$\beta$",r"$\phi$",r"$l_0$","$b_0$","SSE"],
columns=['SES', "Holt's","Exponential", "Additive", "Multiplicative"])
results["SES"] = [fit1.params[p] for p in params] + [fit1.sse]
results["Holt's"] = [fit2.params[p] for p in params] + [fit2.sse]
results["Exponential"] = [fit3.params[p] for p in params] + [fit3.sse]
results["Additive"] = [fit4.params[p] for p in params] + [fit4.sse]
results["Multiplicative"] = [fit5.params[p] for p in params] + [fit5.sse]
results
# [Out]
# SES Holt's Exponential Additive Multiplicative
# 𝛼 0.306282 0.053290 1.655513e-08 0.064947 0.040053
# 𝛽 NaN 0.053290 1.187778e-08 0.064947 0.040053
# 𝜙 NaN NaN NaN 0.995000 0.995000
# 𝑙0 3.487287 3.279317 3.681273e+00 3.234974 3.382898
# 𝑏0 NaN 0.045952 1.009056e+00 0.052515 1.016242
# SSE 692.195826 631.551871 5.823167e+02 641.058197 621.344891
계절성(seasonality)을 포함한 지수평활법에 대해서는 statsmodels.tsa.holtwinters 내의 메소드를 사용해서 시계열 예측 모델을 적합해보겠습니다.
seasonal_periods 에는 계절 주기를 입력해주는데요, 이번 예제에서는 월 단위 집계 데이터에서 1년 단위로 계절성이 나타나고 있으므로 seasonal_periods = 12 를 입력해주었습니다.
trend = 'add' 로 일단 고정을 했으며, 대신에 계절성의 경우 (f) seasonal = 'add' (or 'additive'), (g) seasonal = 'mul' (or 'multiplicative') 로 구분해서 모델을 각각 적합해보았습니다.
위의 시계열 시도표를 보면 시간이 흐름에 따라 분산이 점점 커지고 있으므로 seasonal = 'mul' (or 'multiplicative') 가 더 적합할 것이라고 우리는 예상할 수 있습니다. 실제 그런지 데이터로 확인해보겠습니다.
## Holt's Winters's method for time series data with Seasonality
from statsmodels.tsa.holtwinters import ExponentialSmoothing as HWES
# additive model for fixed seasonal variation
fit6 = HWES(df_train,
seasonal_periods=12,
trend='add',
seasonal='add').fit(optimized=True, use_brute=True)
# multiplicative model for increasing seasonal variation
fit7 = HWES(df_train,
seasonal_periods=12,
trend='add',
seasonal='mul').fit(optimized=True, use_brute=True)
(2) 지수평활법 적합 모델로 예측하여 모델 간 성능 평가/비교하고 최적 모델 선택하기
(forecasting using the exponential smoothing models, model evaluation/ model comparison and best model selection)
(2-1) 향후 12개월 약 판매량 예측하기 (forecasting the drug sales for the next 12 months)
forecast() 함수를 사용하며, 괄호 안에는 예측하고자 하는 기간을 정수로 입력해줍니다.
## forecasting for 12 months
forecast_1 = fit1.forecast(12)
forecast_2 = fit2.forecast(12)
forecast_3 = fit3.forecast(12)
forecast_4 = fit4.forecast(12)
forecast_5 = fit5.forecast(12)
forecast_6 = fit6.forecast(12)
forecast_7 = fit7.forecast(12
y_test = df_test['value']
t_p = pd.DataFrame({'test': y_test,
'f1': forecast_1,
'f2': forecast_2,
'f3': forecast_3,
'f4': forecast_4,
'f5': forecast_5,
'f6': forecast_6,
'f7': forecast_7})
print(t_p)
# test f1 f2 f3 f4 f5 \
# 2007-07-01 21.834890 20.15245 20.350267 20.970823 20.454211 20.261185
# 2007-08-01 23.930204 20.15245 20.511013 21.160728 20.616026 20.421627
# 2007-09-01 22.930357 20.15245 20.671760 21.352352 20.777032 20.582528
# 2007-10-01 23.263340 20.15245 20.832507 21.545711 20.937233 20.743882
# 2007-11-01 25.250030 20.15245 20.993254 21.740821 21.096633 20.905686
# 2007-12-01 25.806090 20.15245 21.154000 21.937699 21.255236 21.067932
# 2008-01-01 29.665356 20.15245 21.314747 22.136359 21.413046 21.230618
# 2008-02-01 21.654285 20.15245 21.475494 22.336818 21.570067 21.393736
# 2008-03-01 18.264945 20.15245 21.636241 22.539092 21.726303 21.557283
# 2008-04-01 23.107677 20.15245 21.796987 22.743198 21.881758 21.721254
# 2008-05-01 22.912510 20.15245 21.957734 22.949152 22.036435 21.885642
# 2008-06-01 19.431740 20.15245 22.118481 23.156972 22.190339 22.050443
# f6 f7
# 2007-07-01 20.882394 21.580197
# 2007-08-01 22.592307 22.164134
# 2007-09-01 21.388974 22.136953
# 2007-10-01 25.178594 24.202879
# 2007-11-01 26.776556 25.322929
# 2007-12-01 26.424404 27.549045
# 2008-01-01 30.468546 31.194773
# 2008-02-01 19.065461 18.181477
# 2008-03-01 21.834584 21.034783
# 2008-04-01 19.061426 20.085947
# 2008-05-01 23.452042 23.076423
# 2008-06-01 22.353486 22.598155
(2-2) 모델 간 모델적합도/성능 평가하고 비교하기
Python의 scikit-learn 라이브러리의 metrics 메소드에 이미 정의되어 있는 MSE, MAE 지표는 가져다가 쓰구요, 없는 지표는 모델 적합도 (goodness-of-fit of time series model)를 평가하는 지표 (https://rfriend.tistory.com/667) 포스팅에서 소개했던 수식대로 Python 사용자 정의 함수(User Defined Funtion)을 만들어서 사용하겠습니다.
아래의 모델 성능 평가 지표 중에서 AIC, SBC, APC, Adjsted-R2 지표는 모델 적합에 사용된 모수의 개수 (the number of parameters) 를 알아야지 계산할 수 있으며, 모수의 개수는 지수평활법 모델 종류별로 다르므로, 적합된 모델 객체로부터 모수 개수를 세는 사용자 정의함수를 먼저 정의해보겠습니다.
## UDF for counting the number of parameters in model
def num_params(model):
n_params = 0
for p in list(model.params.values()):
if isinstance(p, np.ndarray):
n_params += len(p)
#print(p)
elif p in [np.nan, False, None]:
pass
elif np.isnan(float(p)):
pass
else:
n_params += 1
#print(p)
return n_params
num_params(fit1)
[Out] 2
num_params(fit7)
[Out] 17
이제 각 지표별로 Python을 사용해서 지수평활법 모델별로 성능을 평가하는 사용자 정의함수를 정의해보겠습니다. MSE와 MAE는 scikit-learn.metrics 에 있는 메소드를 가져다가 사용하며, 나머지는 공식에 맞추어서 정의해주었습니다.
(혹시 sklearn 라이브러리에 모델 성능 평가 지표 추가로 더 있으면 그거 가져다 사용하시면 됩니다. 저는 sklearn 튜토리얼 찾아보고 없는거 같아서 아래처럼 정의해봤어요. 혹시 코드 잘못된거 있으면 댓글에 남겨주시면 감사하겠습니다.)
## number of observations in training set
T = df_train.shape[0]
print(T)
[Out] 192
## evaluation metrics
from sklearn.metrics import mean_squared_error as MSE
from sklearn.metrics import mean_absolute_error as MAE
# Mean Absolute Percentage Error
def SSE(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.sum((y_test - y_pred)**2)
def ME(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.mean(y_test - y_pred)
def RMSE(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.sqrt(np.mean((y_test - y_pred)**2))
#return np.sqrt(MSE(y_test - y_pred))
def MPE(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.mean((y_test - y_pred) / y_test) * 100
def MAPE(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.mean(np.abs((y_test - y_pred) / y_test)) * 100
def AIC(y_test, y_pred, T, model):
y_test, y_pred = np.array(y_test), np.array(y_pred)
sse = np.sum((y_test - y_pred)**2)
#T = len(y_train) # number of observations
k = num_params(model) # number of parameters
return T * np.log(sse/T) + 2*k
def SBC(y_test, y_pred, T, model):
y_test, y_pred = np.array(y_test), np.array(y_pred)
sse = np.sum((y_test - y_pred)**2)
#T = len(y_train) # number of observations
k = num_params(model) # number of parameters
return T * np.log(sse/T) + k * np.log(T)
def APC(y_test, y_pred, T, model):
y_test, y_pred = np.array(y_test), np.array(y_pred)
sse = np.sum((y_test - y_pred)**2)
#T = len(y_train) # number of observations
k = num_params(model) # number of parameters
return ((T+k)/(T-k)) * sse / T
def ADJ_R2(y_test, y_pred, T, model):
y_test, y_pred = np.array(y_test), np.array(y_pred)
sst = np.sum((y_test - np.mean(y_test))**2)
sse = np.sum((y_test - y_pred)**2)
#T = len(y_train) # number of observations
k = num_params(model) # number of parameters
r2 = 1 - sse/sst
return 1 - ((T - 1)/(T - k)) * (1 - r2)
## Combining all metrics together
def eval_all(y_test, y_pred, T, model):
sse = SSE(y_test, y_pred)
mse = MSE(y_test, y_pred)
rmse = RMSE(y_test, y_pred)
me = ME(y_test, y_pred)
mae = MAE(y_test, y_pred)
mpe = MPE(y_test, y_pred)
mape = MAPE(y_test, y_pred)
aic = AIC(y_test, y_pred, T, model)
sbc = SBC(y_test, y_pred, T, model)
apc = APC(y_test, y_pred, T, model)
adj_r2 = ADJ_R2(y_test, y_pred, T, model)
return [sse, mse, rmse, me, mae, mpe, mape, aic, sbc, apc, adj_r2]
위에서 정의한 시계열 예측 모델 성능평가 지표 사용자 정의 함수를 모델 성능 평가를 위해 따로 떼어놓았던 'test set' 에 적용하여 각 지수평활법 모델별/ 모델 성능평가 지표 별로 비교를 해보겠습니다.
모델 성능평가 지표 중에서 실제값과 예측값의 차이인 잔차(residual)를 기반으로 한 MSE, RMSE, ME, MAE, MPE, MAPE, AIC, SBC, APC 는 낮을 수록 상대적으로 더 좋은 모델이라고 평가할 수 있으며, 실제값과 평균값의 차이 중에서 시계열 예측 모델이 설명할 수 있는 부분의 비중 (모델의 설명력) 을 나타내는 Adjusted-R2 는 값이 높을 수록 상대적으로 더 좋은 모델이라고 평가합니다. (Ajd.-R2 가 음수가 나온 값이 몇 개 보이는데요, 이는 예측 모델이 불량이어서 예측값이 실제값과 차이가 큼에 따라 SSE가 SST보다 크게 되었기 때문입니다.)
eval_all_df = pd.DataFrame(
{'SES': eval_all(y_test, forecast_1, T, fit1),
"Holt's": eval_all(y_test, forecast_2, T, fit2),
'Exponential': eval_all(y_test, forecast_3, T, fit3),
'Trend_Add': eval_all(y_test, forecast_4, T, fit4),
'Trend_Mult': eval_all(y_test, forecast_5, T, fit5),
'Trend_Season_Add': eval_all(y_test, forecast_6, T, fit6),
'Trend_Season_Mult': eval_all(y_test, forecast_7, T, fit7)}
, index=['SSE', 'MSE', 'RMSE', 'ME', 'MAE', 'MPE', 'MAPE', 'AIC', 'SBC', 'APC', 'Adj_R2'])
print(eval_all_df)
# SES Holt's Exponential Trend_Add Trend_Mult \
# SSE 205.629692 155.645609 130.567477 150.867568 159.856508
# MSE 17.135808 12.970467 10.880623 12.572297 13.321376
# RMSE 4.139542 3.601454 3.298579 3.545744 3.649846
# ME 3.018502 1.936578 1.123475 1.841425 2.019134
# MAE 3.453205 2.946251 2.576567 2.878085 3.004307
# MPE 11.739201 6.900165 3.313095 6.486233 7.259990
# MAPE 14.079695 12.280881 10.960354 12.010763 12.510302
# AIC 17.167661 -32.303428 -66.036202 -36.289847 -25.178006
# SBC 23.682652 -19.273447 -53.006220 -20.002370 -8.890530
# APC 1.093535 0.845150 0.708977 0.827788 0.877109
# Adj_R2 -1.146688 -0.642161 -0.377571 -0.600262 -0.695608
# Trend_Season_Add Trend_Season_Mult
# SSE 56.743149 48.994715
# MSE 4.728596 4.082893
# RMSE 2.174533 2.020617
# ME -0.118946 -0.089689
# MAE 1.863421 1.641140
# MPE -0.847971 -0.607618
# MAPE 8.538100 7.461092
# AIC -200.040404 -228.230323
# SBC -144.662983 -172.852902
# APC 0.352956 0.304759
# Adj_R2 0.356850 0.444674
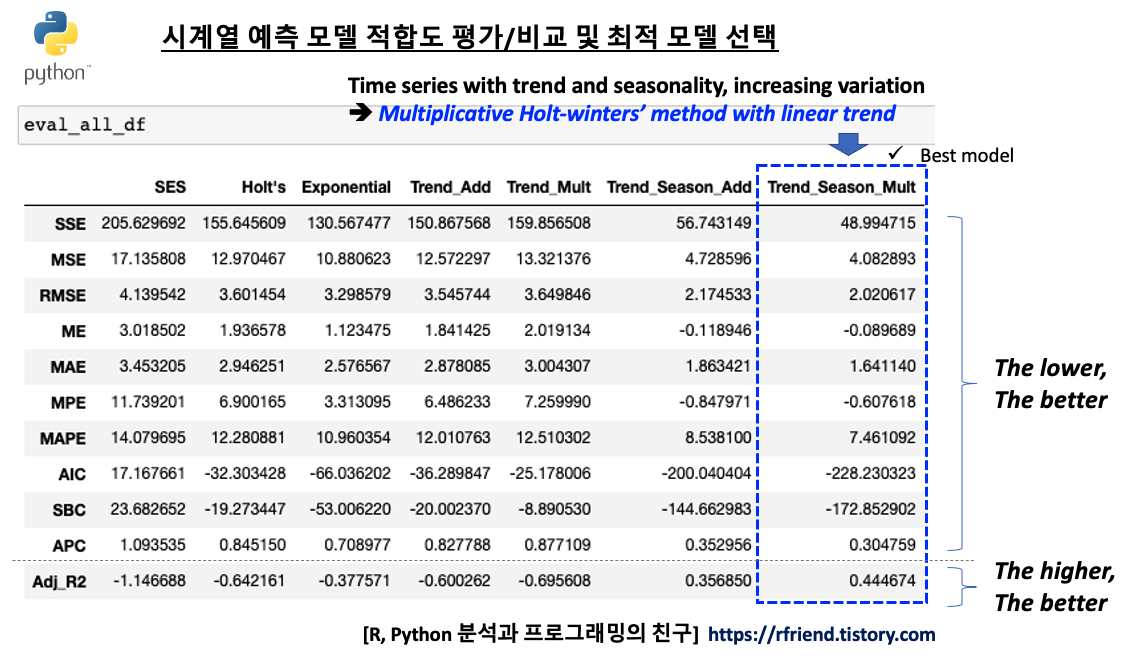
시계열 모델 성능 지표별로 보면 전반적으로 7번째 지수평활법 시계열 예측 모델인 "Multiplicative Winters' method with Linear Trend" 모델이 상대적으로 가장 우수함을 알 수 있습니다. 역시 시도표를 보고서 우리가 예상했던대로 결과가 나왔습니다.
MAPE (Mean Absolute Percentage Error) 지표에 대해서만 옆으로 누운 막대그래프로 모델 간 성능을 비교해서 시각화를 해보면 아래와 같습니다. (MAPE 값이 작을수록 상대적으로 더 우수한 모델로 해석함.)
# horizontal bar chart
eval_all_df.loc['MAPE', :].plot(kind='barh', figsize=[8, 6])
plt.title('Mean Absolute Percentage Error (MAPE)', fontsize=16)
plt.show()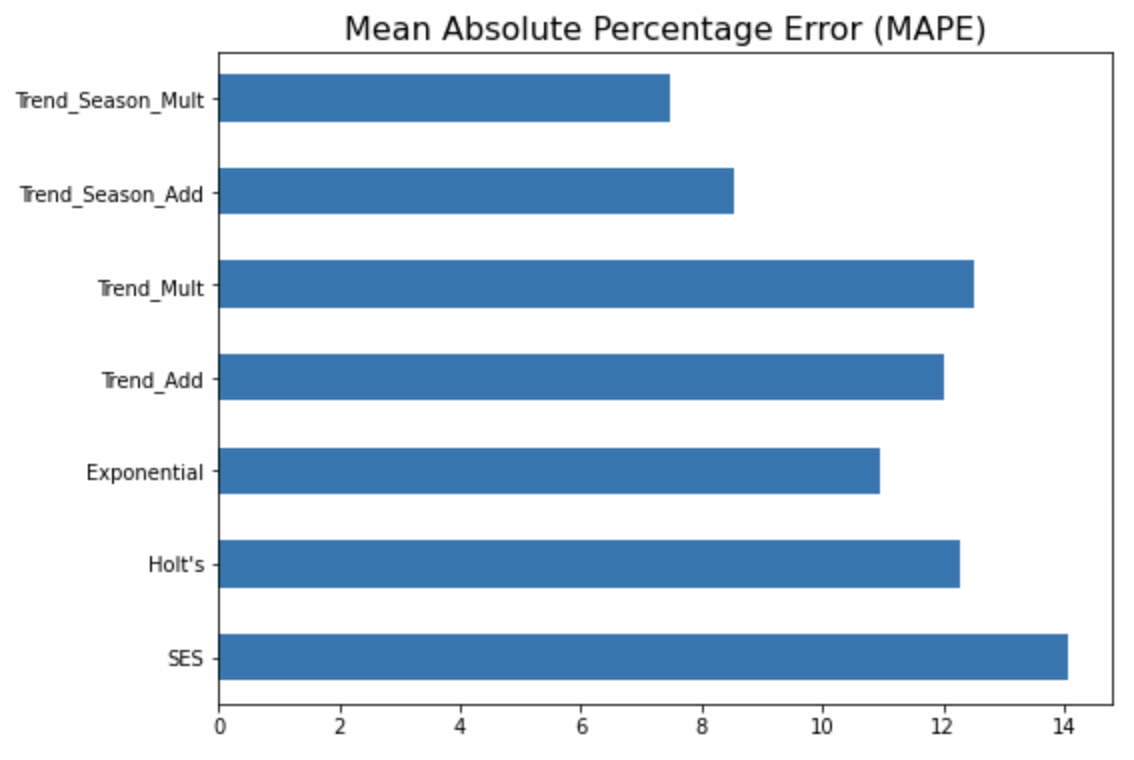
아래의 시도표는 실제값과 예측값을 시간의 흐름에 따라 선그래프로 시각화해 본 것입니다.
예상했던 대로 4번째의 "1차 선형 추세만 반영하고 계절성은 없는 이중 지수 평활법 모델" 보다는, 7번째의 "선형추세+계절성까지 반영한 multiplicative holt-winters method exponential smoothing with linear trend 지수평활법 모델" 이 더 실제값을 잘 모델링하여 근접하게 예측하고 있음을 눈으로 확인할 수 있습니다.
# 1차 선형 추세는 있고 계절성은 없는 이중 지수 평활법
plt.rcParams['figure.figsize']=[12, 8]
past, = plt.plot(df_train.index, df_train, 'b.-', label='Sales History')
test, = plt.plot(df_test.index, df_test, 'r.-', label='y_test')
pred, = plt.plot(df_test.index, forecast_4, 'y.-', label='y_pred')
plt.title('Two Parameter Exponential Smoothing', fontsize=14)
plt.legend(handles=[past, test, pred])
plt.show()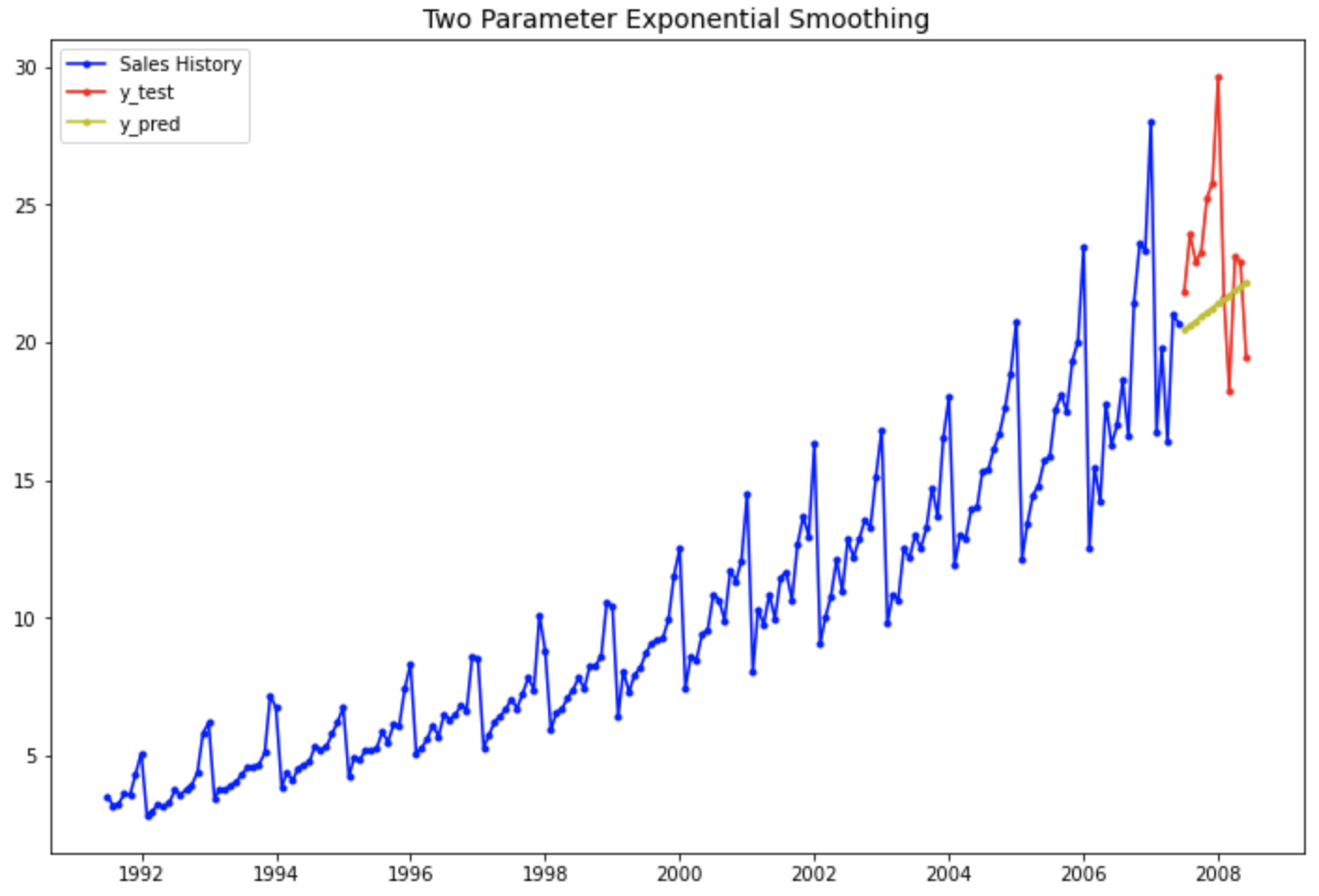
# 1차 선형 추세와 확산계절변동이 있는 승법 윈터스 지수평활법
plt.rcParams['figure.figsize']=[12, 8]
past, = plt.plot(df_train.index, df_train, 'b.-', label='Sales History')
test, = plt.plot(df_test.index, df_test, 'r.-', label='y_test')
pred, = plt.plot(df_test.index, forecast_7, 'y.-', label='y_pred')
plt.title('Multiplicative Winters Method Exponential Smoothing with Linear Trend', fontsize=14)
plt.legend(handles=[past, test, pred])
plt.show()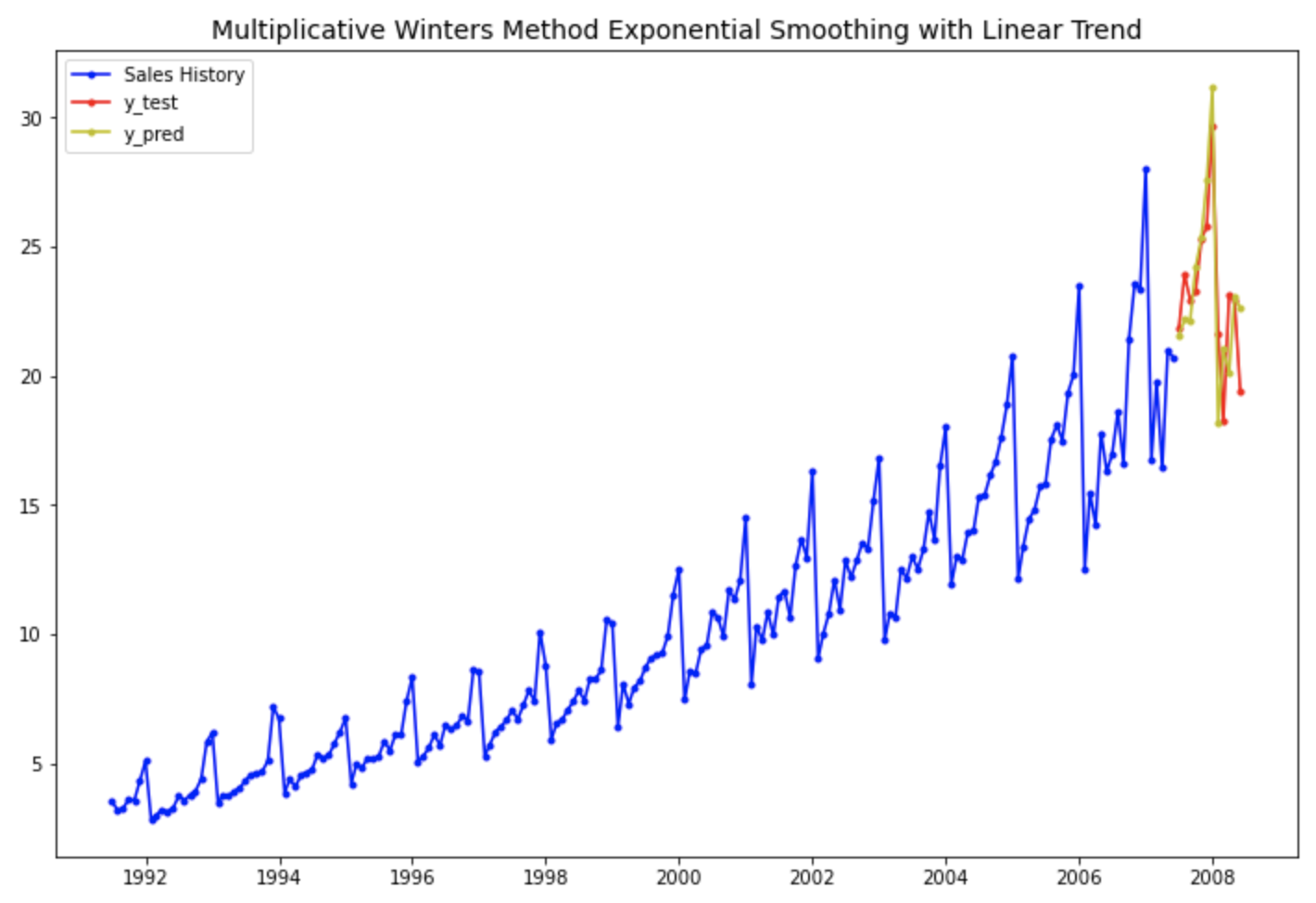
적합된 statsmodels.tsa 시계열 예측 모델에 대해 summary() 메소드를 사용해서 적합 결과를 조회할 수 있으며, model.params['param_name'] 으로 적합된 모델의 속성값에 접근할 수 있습니다.
#print out the training summary
print(fit7.summary())
# ExponentialSmoothing Model Results
# ================================================================================
# Dep. Variable: value No. Observations: 192
# Model: ExponentialSmoothing SSE 75.264
# Optimized: True AIC -147.808
# Trend: Additive BIC -95.688
# Seasonal: Multiplicative AICC -143.854
# Seasonal Periods: 12 Date: Thu, 29 Jul 2021
# Box-Cox: False Time: 19:40:52
# Box-Cox Coeff.: None
# =================================================================================
# coeff code optimized
# ---------------------------------------------------------------------------------
# smoothing_level 0.2588475 alpha True
# smoothing_trend 0.0511336 beta True
# smoothing_seasonal 3.3446e-16 gamma True
# initial_level 2.1420252 l.0 True
# initial_trend 0.0466926 b.0 True
# initial_seasons.0 1.4468847 s.0 True
# initial_seasons.1 1.4713123 s.1 True
# initial_seasons.2 1.4550909 s.2 True
# initial_seasons.3 1.5754307 s.3 True
# initial_seasons.4 1.6324776 s.4 True
# initial_seasons.5 1.7590615 s.5 True
# initial_seasons.6 1.9730448 s.6 True
# initial_seasons.7 1.1392096 s.7 True
# initial_seasons.8 1.3057795 s.8 True
# initial_seasons.9 1.2354317 s.9 True
# initial_seasons.10 1.4064560 s.10 True
# initial_seasons.11 1.3648905 s.11 True
# ---------------------------------------------------------------------------------
print('Smoothing Level: %.3f' %(fit7.params['smoothing_level']))
print('Smoothing Trend: %.3f' %(fit7.params['smoothing_trend']))
print('Smoothing Seasonality: %.3f' %(fit7.params['smoothing_seasonal']))
print('Initial Level: %.3f' %(fit7.params['initial_level']))
print('Initial Trend: %.3f' %(fit7.params['initial_trend']))
print('Initial Seasons:', fit7.params['initial_seasons'])
# Smoothing Level: 0.259
# Smoothing Trend: 0.051
# Smoothing Seasonality: 0.000
# Initial Level: 2.142
# Initial Trend: 0.047
# Initial Seasons: [1.44688473 1.47131227 1.45509092 1.5754307 1.63247755 1.75906148
# 1.97304481 1.13920961 1.30577953 1.23543175 1.40645604 1.36489053]
[Reference]
* Exponential Smoothing
: https://www.statsmodels.org/stable/examples/notebooks/generated/exponential_smoothing.html
* Holt-Winters
: https://www.statsmodels.org/devel/generated/statsmodels.tsa.holtwinters.ExponentialSmoothing.html
Exponential smoothing — statsmodels
Exponential smoothing Let us consider chapter 7 of the excellent treatise on the subject of Exponential Smoothing By Hyndman and Athanasopoulos [1]. We will work through all the examples in the chapter as they unfold. [1] [Hyndman, Rob J., and George Athan
www.statsmodels.org
statsmodels.tsa.holtwinters.ExponentialSmoothing — statsmodels
An dictionary containing bounds for the parameters in the model, excluding the initial values if estimated. The keys of the dictionary are the variable names, e.g., smoothing_level or initial_slope. The initial seasonal variables are labeled initial_season
www.statsmodels.org
* 시계열 패턴 별 지수평활법 모델을 설정하는 방법
: https://rfriend.tistory.com/511
* 시계열 데이터 예측 모델의 성능, 모델 적합도 (goodness-of-fit of time series model)를 평가하는 지표
: https://rfriend.tistory.com/667
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)











