[Python] 통계에서 p-값은 무엇이고, 어떻게 해석하는가? (p-value in statistics)
Python 분석과 프로그래밍/Python 통계분석 2023. 12. 8. 15:32이번 포스팅에서는 통계학에서 사용하는 p-값(p-value)이란 무엇이고, 어떻게 해석하는지 소개하겠습니다.
1. 통계학에서 p-value 는 무엇이며, 무엇에 사용하는가?
2. 독립된 두 표본 간 평균 차이 t-검정에서 p-value 해석 예시
3. Python으로 독립 두 표본 t-검정 (independent two-sample t-test)
4. 빈도론자(Frequentist)와 베이지안(Bayesian) 간 p-value 해석의 차이점은 무엇인가?
1. 통계학에서 p-value 는 무엇이며, 무엇에 사용하는가?
통계학에서 p-값(확률 값)은 귀무가설(null hypothesis, H0)에 대한 증거를 평가하는 데 도움이 되는 지표입니다. 귀무가설은 차이나 효과가 없다는 것을 나타내는 명제로, 연구자들은 이 귀무가설을 기각할 충분한 증거가 있는지를 판단하기 위해 통계 검정을 사용합니다.
p-값은 귀무가설이 참일 때 관측 결과나 그보다 더 극단적인 결과가 나올 확률을 나타냅니다. 다시 말해, 이는 귀무가설에 대한 증거의 강도를 측정하는 것입니다.
주로 다음과 같은 방식으로 사용합니다.
(1) 만약 p-값이 작다면(일반적으로 미리 정의된 유의수준, 예를 들어 0.05보다 낮다면), 이는 관측 결과가 무작위로 발생할 가능성이 적다는 것을 나타내며, 이는 귀무가설(null hypothesis, H0)을 기각하고 대립가설(alternative hypothesis, H1)을 채택합니다.
(2) 만약 p-값이 크다면, 이는 관측 결과가 귀무가설과 상당히 일치한다는 것을 나타내며, 귀무가설을 기각할 충분한 증거가 없다는 것을 의미합니다.
p-값이 작다고 해서 특정 가설이 참임을 증명하는 것은 아닙니다. 이는 단순히 데이터가 귀무가설과 일치하지 않는다는 것을 나타냅니다. 또한, 유의수준(예: 0.05)의 선택은 어느 정도 임의적이며 연구자의 판단이나 해당 분야의 관례에 따라 달라집니다.
연구자들은 p-값을 신중하게 해석하고 귀무가설 검정에 관한 결정을 내릴 때 다른 관련 정보와 함께 고려해야 합니다. p-값은 효과의 크기나 실제적인 중요성에 대한 정보를 제공하지 않으며, 단지 귀무가설에 대한 증거의 강도(the evidence against a null hypothesis)를 나타냅니다.
2. 독립된 두 표본 간 평균 차이 t-검정에서 p-value 해석 예시
예를 들어 혈압을 낮추는 새로운 약물에 대한 임상시험을 다루는 예를 살펴보겠습니다. 연구자들은 새로운 약물이 플라시보에 비해 혈압을 낮추는 데 효과적인지를 테스트하고자 합니다. 이 맥락에서 p-값의 사용과 해석은 다음과 같을 수 있습니다.
시나리오:
- 귀무가설 (H0): 새로운 약물은 혈압에 아무런 영향을 미치지 않으며, 관측된 차이는 무작위로 발생한 것이다.
- 대립가설 (H1): 새로운 약물은 플라시보에 비해 혈압을 낮추는 데 효과적이다. 즉, 플라시보 그룹보다 신약 그룹의 혈압이 더 낮다.
실험 설계:
- 연구자들은 참가자들을 새로운 약물을 받는 그룹과 플라시보를 받는 그룹으로 무작위로 배정합니다.
- 특정한 치료 기간 이후 각 참가자의 혈압 변화를 측정합니다.
데이터 분석:
- 각 10개의 샘플 데이터를 수집하고 분석한 후, 연구자들은 두 그룹 간의 혈압 변화의 평균을 비교하기 위해 통계적 검정(예: t-검정)을 수행합니다.
- 예를 들어, 검정 결과로 얻은 t-통계량이 3.372, p-값이 0.0017인 경우를 가정해 봅시다.
해석:
- 얻은 p-값(0.0034)이 선택된 유의수준(예: alpah=0.05)보다 작습니다.
- 빈도주의적 해석: 이는 만약 귀무가설이 사실이라면(즉, 새로운 약물이 효과가 없다면), 실제로 관측된 데이터보다 더 극단적인 데이터를 관측할 확률이 0.17%밖에 되지 않는다는 것을 나타냅니다. 0.0017이 유의수준 0.05 보다 작으므로 연구자들은 귀무가설을 기각하기로 결정할 수 있습니다.
- 결정: 연구자들은 귀무가설을 기각하고 새로운 약물이 플라시보에 비해 혈압을 낮추는 데 효과적임을 시사하는 충분한 증거가 있다고 결론지을 수 있습니다.
아래에는 t-분포표를 수작업으로 해석하는 방법입니다.
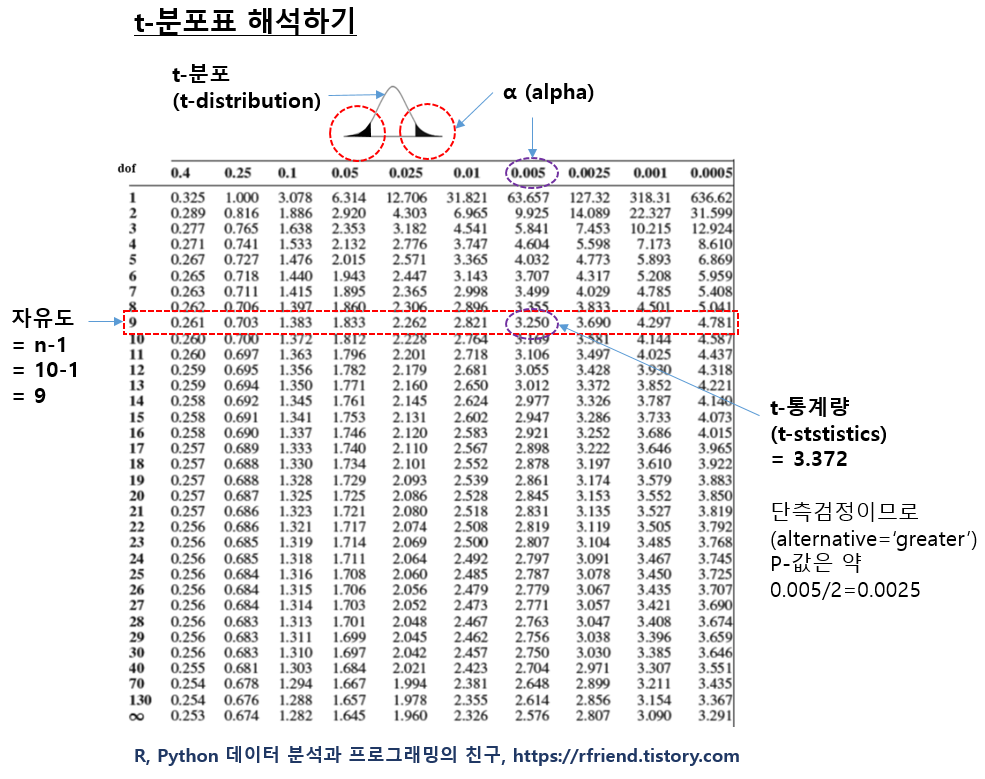
t-분포표의 행은 자유도(degree of freedom) 으로서, 만약 샘플의 관측치 개수가 주어지면 (자유도 = n-1) 로 계산해줍니다. t-분포표의 열은 유의수준 알파(alpha)이고, 표의 안에 있는 숫자는 가설 검정에 사용하는 t-통계량입니다. (정규분포표에서는 행과 열이 z-통계량이고, 표의 가운데 값이 p-value인데요, t-분포표는 이와 달라서 좀 헷갈리는 면이 있습니다.) 샘플로 부터 자유도와 t-통계량를 계산하면, 아래의 t-분포표를 보고 상단 열에서 p-값을 찾으면 됩니다.
이번 예에서는 가령, 관측치가 각 그룹별로 10개라고 하면, 자유도 = n-1 = 9 가 됩니다.
그리고 t-통계량을 계산했더니 3.372가 나왔다고 했을 때, 아래 표에서 t-통계량 3.372 는 자유도 9인 행에서 보면 3.250보다는 크고, 3.690보다는 작은 값입니다. 따라서 상단의 알파(alpha) 값은 0.005와 0.0025 사이의 값이라고 추정할 수 있습니다. 그런데 대립가설이 "H1: 새로운 약물은 플라시보에 비해 혈압을 낮추는 데 효과적이다. 즉, 플라시보 그룹보다 신약 그룹의 혈압이 더 낮다." 이므로 단측검정 (alternative = 'greater') 을 사용하므로, p-value=0.005/2=0.0025 보다 작고 ~ p-value=0.0025/2=0.00125 보다는 큰 값으로 볼 수 있습니다.
유의수준 0.05보다는 훨씬 작은 값이므로, 귀무가설을 기각하고 대립가설을 채택합니다. 즉, 신약이 혈압을 낮추는데 효과가 있다고 판단할 수 있습니다.
p-값 자체만으로는 효과의 크기나 임상적 중요성에 대한 정보를 제공하지 않습니다. 연구자들은 통계 검정을 기반으로 의사결정을 내릴 때 효과 크기, 신뢰구간 및 실제적인 중요성도 고려해야 합니다. 또한 베이지안 프레임워크에서는 관측된 데이터를 기반으로 사전 신념을 업데이트하는 것이 포함될 수 있습니다.
3. Python으로 독립 두 표본 t-검정 (independent two-sample t-test)
scipy 모듈의 scipy.stats.stats.ttest_ind() 메소드를 사용해서 독립된 두 표본의 평균에 차이가 있는지를 t-검정해 보겠습니다.
- 귀무가설(H0): Group 1과 Group 2의 평균에는 차이가 없다. (mu_g1 = mu_g2)
- 대립가설(H1): Group 1가 Group 2의 평균보다 크다. (mu_g1 > mu_g2)
t 통계량이 3.37이고 p-값(p-value)이 0.0034 로서, 유의수준(alpha) 0.05보다 p-값이 더 작으므로 귀무가설을 기각(reject null hypothesis)하고, 대립가설을 채택(accept alternative hypothesis)합니다.
## independent two-sample t-test
import numpy as np
import scipy.stats as stats
# Example data for two independent samples
group1 = [25, 30, 32, 28, 34, 26, 30, 29, 31, 27]
group2 = [21, 24, 28, 25, 30, 22, 26, 23, 27, 24]
print('Mean of Group 1:', np.mean(group1))
print('Mean of Group 2:', np.mean(group2))
# Perform independent two-sample t-test
t_statistic, p_value = stats.ttest_ind(
group1, group2,
equal_var=True,
alternative='greater', # alternative hypothesis: mu_1 is greater than mu_2
)
# Print the results
print(f'T-statistic: {t_statistic}')
print(f'P-value: {p_value}')
# Check the significance level (e.g., 0.05)
alpha = 0.05
if p_value < alpha:
print('Reject the null hypothesis. \
There is a significant difference between the groups.')
else:
print('Fail to reject the null hypothesis. \
There is no significant difference between the groups.')
# Mean of Group 1: 29.2
# Mean of Group 2: 25.0
# T-statistic: 3.3723126837047914
# P-value: 0.0016966232763530164
# Reject the null hypothesis. There is a significant difference between the groups.
4. 빈도론자(Frequentist)와 베이지안(Bayesian) 간 p-value 해석의 차이점은 무엇인가?
빈도론자(Frequentist)와 베이지안(Bayesian) 간의 통계학적 접근 방식에서 p-값의 해석은 다릅니다. 각 접근 방식이 p-값을 어떻게 해석하는지 간략하게 살펴보겠습니다.
(1) 빈도주의적 해석 (Frequentist Interpretation):
- 빈도주의 통계학에서 p-값은 귀무가설이 참일 때 관측된 데이터나 그보다 더 극단적인 데이터가 나올 확률로 간주됩니다.
- 의사결정 과정은 일반적으로 특정한 유의수준(alpha), 보통 0.05,을 기준으로 귀무가설을 기각하거나 기각하지 않는 것으로 구성됩니다.
- 만약 p-값이 선택된 유의수준보다 작거나 같으면 귀무가설이 기각됩니다. p-값이 유의수준보다 크면 귀무가설이 기각되지 않습니다.
- 빈도주의 통계학에서는 확률을 가설에 할당하지 않으며 대신 특정 가설 하에서 데이터의 확률에 중점을 둡니다.
(2) 베이지안 해석 (Bayesian Interpretation):
- 베이지안 통계학에서는 관측된 데이터를 기반으로 가설에 대한 사전 신념(prior beliefs)을 업데이트하는 것에 중점을 둡니다.
- 베이지안 분석은 가설에 대한 사전 신념과 관측된 데이터 모두를 고려하여 가설에 대한 사후 확률 분포(posterior probability distribution for the hypothesis)를 제공합니다.
- 베이지안은 의사결정을 위해 일반적으로 p-값 만을 고려하지 않습니다. 대신 전체 사후 분포를 고려하며 이전 정보를 통합합니다.
- 베이지안 분석은 데이터가 주어졌을 때 가설이 참일 확률을 직접 계산합니다. 이는 빈도주의적 접근과 달리 가설이 주어진 데이터에 대한 확률만을 고려하는 것이 아닙니다.
- 가설 검정을 위해 때로는 베이지안 분석에서는 가설 간의 가능도 비율(ratio of the likehoods under different hypotheses)인 베이즈 팩터(Bayes factor)를 사용하기도 합니다.
요약하면 핵심적인 차이점은 확률 해석에 있습니다. 빈도주의자들은 확률을 사건의 장기적 빈도로 간주하며, 베이지안은 확률을 신념이나 불확실성의 척도로 해석합니다. 빈도주의자들은 p-값을 가설에 대한 의사결정에 사용하며, 베이지안안은 베이지안 추론을 사용하여 직접적으로 신념을 업데이트하고 표현합니다.
이번 포스팅이 많은 도움이 되었기를 바랍니다.

'Python 분석과 프로그래밍 > Python 통계분석' 카테고리의 다른 글
| 베이지안 통계(Bayesian Statistics)와 베이즈 정리(Bayes's Theorem) (1) | 2023.12.09 |
|---|---|
| 중심극한의 정리 (Central Limit Theorem) 이란 무엇이고, 왜 중요한가? (0) | 2023.12.09 |
| [Python] 쌍을 이룬 t-test (paired t-test) (0) | 2022.10.03 |
| [Python] 두 집단 간 평균 차이를 검정하는 t-test (0) | 2022.10.03 |
| [Python] 분산 안정화 변환과 차분으로 정상확률과정으로 변환(variance stabilization transformation and differencing for stationarity) (0) | 2021.10.31 |



