[Python] 주성분분석을 통한 차원 축소 (Dimensionality Reduction using PCA, Principal Component Analysis)
Python 분석과 프로그래밍/Python 기계학습 2022. 9. 4. 22:42지난 포스팅에서는 차원 축소란 무엇이고 왜 하는지, 무슨 방법이 있는지에 대해서 알아보았습니다.
(https://rfriend.tistory.com/736) 차원축소하는 방법에는 크게 Projection-based dimensionality reduction, Manifold Learning 의 두가지 방법이 있다고 했습니다.
이번 포스팅에서는 투사를 통한 차원축소 방법(dimensionality reduction via projection approach) 으로서 주성분분석을 통한 차원축소(dimensionality reduction using PCA, Principal Component Analysis)에 대해서 소개하겠습니다.
(1) 주성분분석(PCA, Principal Component Analysis)을 통한 차원 축소
(2) 특이값 분해 (SVD, Singular Value Decomposition)을 통한 차원 축소
(1) 주성분 분석(PCA, Principal Component Analysis)을 통한 차원 축소
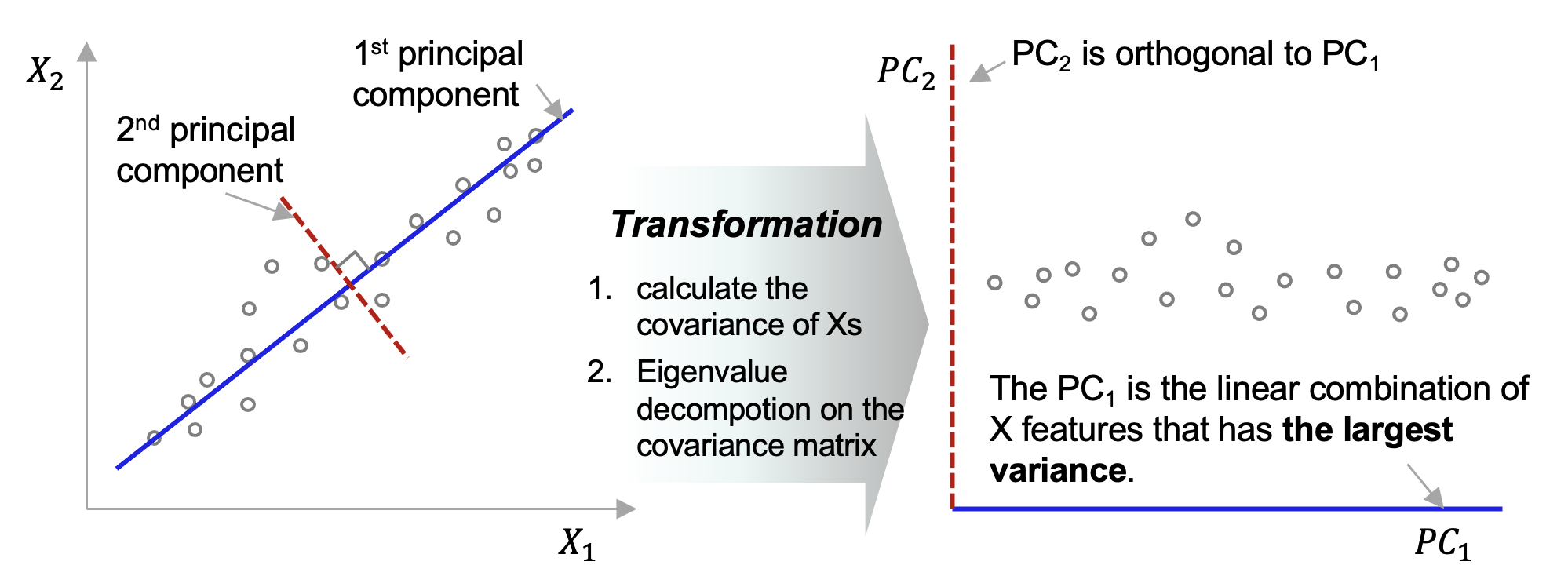
주성분 분석(PCA)의 핵심 아이디어만 간략하게 소개하자면요, 피쳐 공간(Feature Space)에서 데이터의 분산을 최대로 잡아낼 수 있는 축을 제1 주성분 축으로 잡고, 이 제1 주성분 축과 직교(orthogonal)하는 축을 제2 주성분 축으로 잡고, ..., 이렇게 최대 변수의 개수 p 개 만큼 주성분 축을 잡아줍니다. (물론, 차원축소를 하는 목적이면 주성분 개수 m 이 변수 개수 p 보다는 작아야 겠지요). 그리고 축을 회전시켜주면 돼요.
아래의 예시 도면을 보면 파란색 제 1 주성분 축 (1st principal component axis)이 데이터 분산을 가장 많이 설명하고 있는 것을 알 수 있습니다. 빨간색 점선의 제 2 주성분 축(2nd principal component axis) 은 제1 주성분 축과 직교하구요.
이제 Python 을 가지고 실습을 해볼께요.
(R로 주성분 분석 하는 것은 https://rfriend.tistory.com/61 를 참고하세요.)
먼저 예제로 사용할 iris 데이터셋을 가져오겠습니다. sepal_length, sepal_width, petal_length, petal_width 의 4개 변수를 가진 데이터셋인데요, 4개 변수 간 상관관계 분석을 해보니 상관계수가 0.8 이상으로 꽤 높게 나온 게 있네요. 주성분분석으로 차원축소 해보면 이쁘게 나올거 같아요.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
## loading IRIS dataset
from sklearn.datasets import load_iris
data = load_iris()
data['data'][:10]
# array([[5.1, 3.5, 1.4, 0.2],
# [4.9, 3. , 1.4, 0.2],
# [4.7, 3.2, 1.3, 0.2],
# [4.6, 3.1, 1.5, 0.2],
# [5. , 3.6, 1.4, 0.2],
# [5.4, 3.9, 1.7, 0.4],
# [4.6, 3.4, 1.4, 0.3],
# [5. , 3.4, 1.5, 0.2],
# [4.4, 2.9, 1.4, 0.2],
# [4.9, 3.1, 1.5, 0.1]])
## converting into pandas DataFrame
iris_df = pd.DataFrame(
data['data'],
columns=['sepal_length', 'sepal_width',
'petal_length', 'petal_width'])
iris_df.head()
# sepal_length sepal_width petal_length petal_width
# 0 5.1 3.5 1.4 0.2
# 1 4.9 3.0 1.4 0.2
# 2 4.7 3.2 1.3 0.2
# 3 4.6 3.1 1.5 0.2
# 4 5.0 3.6 1.4 0.2
## correlation matrix
iris_df.corr()
# sepal_length sepal_width petal_length petal_width
# sepal_length 1.000000 -0.117570 0.871754 0.817941
# sepal_width -0.117570 1.000000 -0.428440 -0.366126
# petal_length 0.871754 -0.428440 1.000000 0.962865
# petal_width 0.817941 -0.366126 0.962865 1.000000
주성분 분석은 비지도 학습 (Unsupervised Learning) 이다보니 정답이라는게 없습니다. 그래서 분석가가 주성분의 개수를 지정해주어야 하는데요, 주성분의 개수가 적을 수록 차원 축소가 많이 되는 반면 정보 손실(information loss)가 발생하게 되며, 반면 주성분 개수가 많을 수록 정보 손실은 적겠지만 차원 축소하는 의미가 퇴색됩니다. 그래서 적절한 주성분 개수를 선택(hot to decide the number of principal components)하는게 중요한데요, 주성분의 개수별로 설명 가능한 분산의 비율 (percentage of explained variance by principal components) 을 많이 사용합니다.
아래의 예에서는 첫번째 주성분이 분산의 92.4%를 설명하고, 두번째 주성분이 분산의 5.3%를 설명하므로, 주성분 1 & 2 까지 사용하면 전체 분산의 97.7%를 설명할 수 있게 됩니다. (즉, 원래 4개 변수를 2개의 차원으로 축소하더라도 분산의 97.7%를 설명 가능하다는 뜻)
참고로, 만약 주성분분석 결과를 지도학습(가령, 회귀분석)의 설명변수 인풋으로 사용한다면, cross validation을 사용해서 주성분 개수별로 모델의 성능을 평가(가령, 회귀분석의 경우 MSE)해서, 모델 성능지표가 가장 좋은 주성분 개수를 선택하는 것도 좋은 방법입니다.
## how to decide the number of Principal Components
from sklearn.decomposition import PCA
pca = PCA(random_state=1004)
pca.fit_transform(iris_df)
## percentage of variance explained
print(pca.explained_variance_ratio_)
# [0.92461872 0.05306648 0.01710261 0.00521218]
## Principal 1 & 2 explain about 97.8% of variance
plt.rcParams['figure.figsize'] = (7, 7)
plt.plot(range(1, iris_df.shape[1]+1), pca.explained_variance_ratio_)
plt.xlabel("number of Principal Components", fontsize=12)
plt.ylabel("% of Variance Explained", fontsize=12)
plt.show()
이제 주성분 개수를 2개로 지정(n_components=2)해서 주성분 분석을 실행해보겠습니다. Python의 sklearn 모듈의 decomposition.PCA 메소드를 사용하겠습니다.
## Dimensionality Reduction with n_components=2
pca = PCA(n_components=2, random_state=1004)
iris_pca = pca.fit_transform(iris_df)
iris_pca[:10]
# array([[-2.68412563, 0.31939725],
# [-2.71414169, -0.17700123],
# [-2.88899057, -0.14494943],
# [-2.74534286, -0.31829898],
# [-2.72871654, 0.32675451],
# [-2.28085963, 0.74133045],
# [-2.82053775, -0.08946138],
# [-2.62614497, 0.16338496],
# [-2.88638273, -0.57831175],
# [-2.6727558 , -0.11377425]])
위에서 실행한 주성분분석 결과를 가지고 시각화를 해보겠습니다. 4개 변수를 2개의 차원으로 축소를 했기 때문에 2차원의 산점도로 시각화를 할 수 있습니다. 이때 iris 데이터셋의 target 속성정보를 이용해서 붓꽃의 품종별로 색깔과 모양을 달리해서 산점도로 시각화해보겠습니다.
## Visualization
## target
data['target'][:5]
# array([0, 0, 0, 0, 0])
## mapping target name using numpy vectorization
species_map_dict = {
0: 'setosa',
1: 'versicolor',
2: 'virginica'
}
iris_pca_df = pd.DataFrame({
'pc_1': iris_pca[:, 0],
'pc_2': iris_pca[:, 1],
'species': np.vectorize(species_map_dict.get)(data['target']) # numpy broadcasting
})
iris_pca_df.head()
# pc_1 pc_2 species
# 0 -2.684126 0.319397 setosa
# 1 -2.714142 -0.177001 setosa
# 2 -2.888991 -0.144949 setosa
# 3 -2.745343 -0.318299 setosa
# 4 -2.728717 0.326755 setosa
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (7, 7)
sns.scatterplot(
x='pc_1',
y='pc_2',
hue='species',
style='species',
s=100,
data=iris_pca_df
)
plt.title('PCA result of IRIS dataset')
plt.xlabel('Principal Component 1', fontsize=14)
plt.ylabel('Principal Component 2', fontsize=14)
plt.show()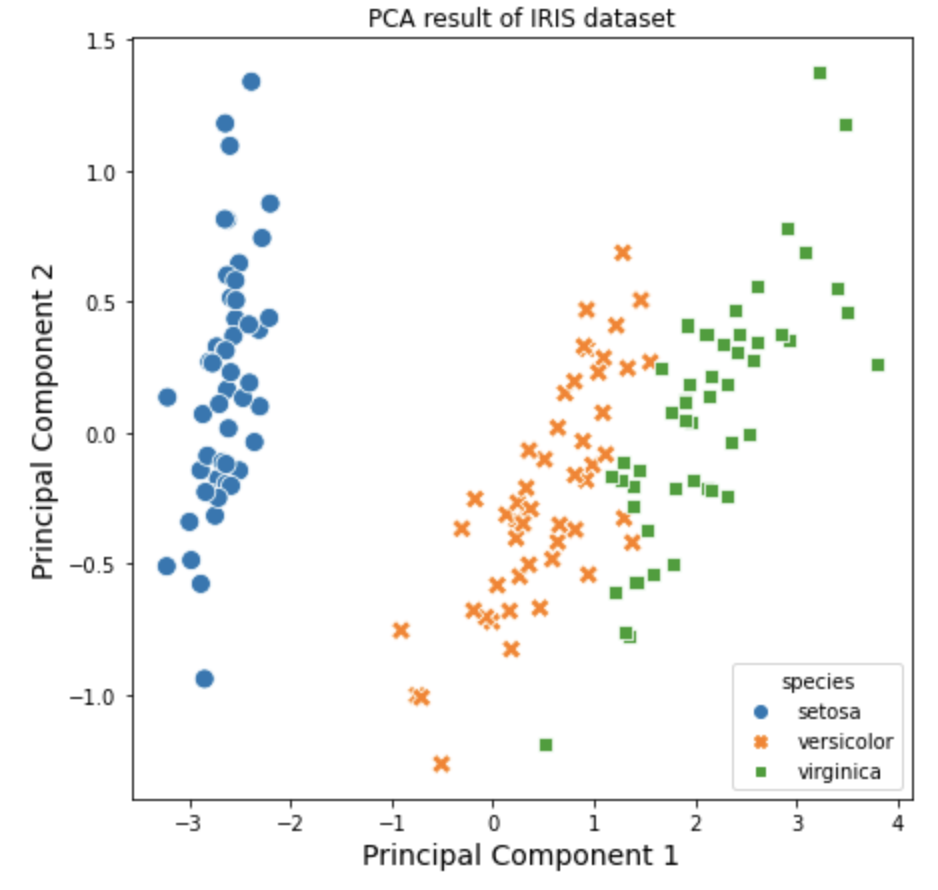
(2) 특이값 분해 (SVD, Singular Value Decomposition)을 통한 차원 축소
선형대수의 특이값 분해의 결과로 나오는 U, sigma, V 에서 V 가 주성분 분석의 주성분에 해당합니다.
특이값 분해(SVD, Singular Value Decomposition)에 대한 이론적인 소개는 https://rfriend.tistory.com/185 를 참고하세요.
numpy 모듈의 linalg.svd 메소드를 사용하여 특이값 분해를 하려고 할 때 먼저 데이터 표준화(standardization)을 수작업으로 진행해 줍니다. (sklearn 으로 주성분분석을 할 때 sklearn 모듈이 내부적으로 알아서 표준화해서 진행해줌).
## Standardization first
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(data['data'])
## PCA assumes that the dataset is centered around the origin.
X_centered = data['data'] - data['data'].mean(axis=0)
X_centered[:5]
# array([[-0.74333333, 0.44266667, -2.358 , -0.99933333],
# [-0.94333333, -0.05733333, -2.358 , -0.99933333],
# [-1.14333333, 0.14266667, -2.458 , -0.99933333],
# [-1.24333333, 0.04266667, -2.258 , -0.99933333],
# [-0.84333333, 0.54266667, -2.358 , -0.99933333]])
웨에서 표준화한 데이터를 numpy 모듈의 linalg.svd 메소드를 사용하여 특이값 분해를 해준 후에, V 를 transpose (T) 해주어서 첫번째와 두번째 열의 값을 가져오면 제1 주성분, 제2 주성분을 얻을 수 있습니다.
## standard matrix factorization using SVD
U, s, V = np.linalg.svd(X_scaled.T)
## V contains all the principal components
pc_1 = V.T[:, 0]
pc_2 = V.T[:, 1]
## check pc_1, pc_2
pc_1[:10]
# array([0.10823953, 0.09945776, 0.1129963 , 0.1098971 , 0.11422046,
# 0.099203 , 0.11681027, 0.10671702, 0.11158214, 0.10439809])
pc_2[:10]
# array([-0.0409958 , 0.05757315, 0.02920003, 0.05101939, -0.0552418 ,
# -0.12718049, -0.00406897, -0.01905755, 0.09525253, 0.04005525])
위에서 특이값분해(SVD)로 구한 제1 주성분, 제2 주성분을 가지고 산점도를 그려보겠습니다. 이때 iris 의 target 별로 색깔과 모양을 달리해서 시각화를 해보겠습니다.
## Visualization
iris_svd_df = pd.DataFrame({
'pc_1': pc_1,
'pc_2': pc_2,
'species': np.vectorize(species_map_dict.get)(data['target']) # numpy broadcasting
})
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (7, 7)
sns.scatterplot(
x='pc_1',
y='pc_2',
hue='species',
style='species',
s=100,
data=iris_svd_df
)
plt.title('SVD result of IRIS dataset')
plt.xlabel('Principal Component 1', fontsize=14)
plt.ylabel('Principal Component 2', fontsize=14)
plt.show()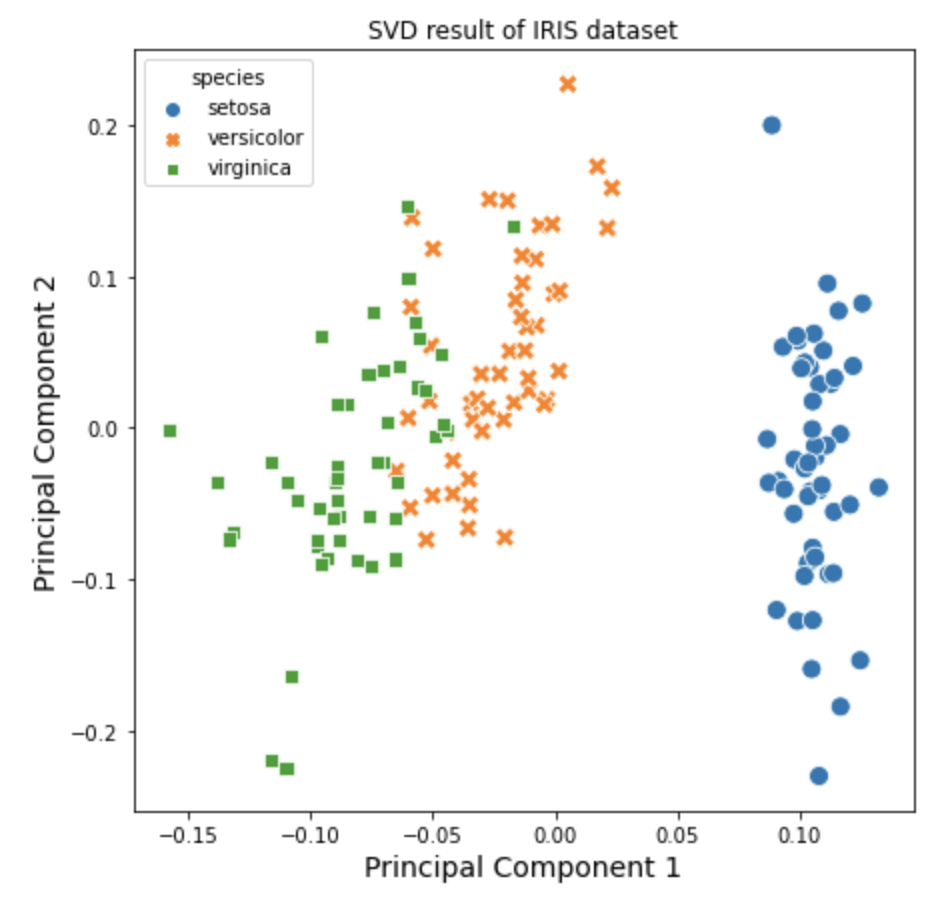
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요.




