이번 포스팅에서는 국가통계포털 사이트에서 받은 2020년, 2021년도 실업률과 취업자 수 통계 데이터를 가지고 R의 dplyr과 ggplot2 패키지를 사용해서 아래의 데이터 전처리 및 시각화하는 방법을 소개하겠습니다.
1. 취업자 수 증가율(%) 변수 계산 (전년 동월 대비)
2. 실업률과 취업자 수 증가율 변수의 평균, 분산, 표준편차, 중앙값, 최대값, 최소값 계산
3. 실업률과 취업자 수 증가율 변수의 시계열 그래프 그리기
4. 실업률과 취업자 수 증가율 변수의 히스토그램 그리기 (히스토그램의 구간은 10개)
먼저, 국가통계포털 사이트에서 받은 2020년, 2021년도 실업률과 취업자 수 통계 데이터를 입력해서 DataFrame을 만들어보겠습니다. 데이터 자료 구조를 어떻게 해서 만드는지 유심히 봐주세요.
## making a dataframe
df <- data.frame(
month=c("01", "02", "03", "04", "05", "06", "07", "08", "09", "10", "11", "12"),
unemploy_rate_2020=c(4.1, 4.1, 4.2, 4.2, 4.5, 4.3, 4.0, 3.1, 3.6, 3.7, 3.4, 4.1),
unemploy_rate_2021=c(5.7, 4.9, 4.3, 4.0, 4.0, 3.8, 3.2, 2.6, 2.7, 2.8, 2.6, 3.5),
employed_num_2020=c(26800, 26838, 26609, 26562, 26930, 27055, 27106, 27085, 27012, 27088, 27241, 26526),
employed_num_2021=c(25818, 26365, 26923, 27214, 27550, 27637, 27648, 27603, 27683, 27741, 27795, 27298)
)
print(df)
# month unemploy_rate_2020 unemploy_rate_2021 employed_num_2020 employed_num_2021
# 1 01 4.1 5.7 26800 25818
# 2 02 4.1 4.9 26838 26365
# 3 03 4.2 4.3 26609 26923
# 4 04 4.2 4.0 26562 27214
# 5 05 4.5 4.0 26930 27550
# 6 06 4.3 3.8 27055 27637
# 7 07 4.0 3.2 27106 27648
# 8 08 3.1 2.6 27085 27603
# 9 09 3.6 2.7 27012 27683
# 10 10 3.7 2.8 27088 27741
# 11 11 3.4 2.6 27241 27795
# 12 12 4.1 3.5 26526 27298
1. 취업자 수 증가율(%) 변수 계산 (전년 동월 대비)
dplyr 패키지로 새로운 변수를 생성하는 방법은 https://rfriend.tistory.com/235 를 참고하세요.
dplyr 패키지의 chain operation, pipe operator %>% 사용 방법은 https://rfriend.tistory.com/236 를 참고하세요.
## 1. 취업자 수 증가율(%) 변수 계산 (전년 동월 대비)
library(dplyr)
df2 <- df %>%
transform(
employed_inc_rate = 100*(employed_num_2021 - employed_num_2020)/employed_num_2020) # percentage
print(df2)
# month unemploy_rate_2020 unemploy_rate_2021 employed_num_2020 employed_num_2021 employed_inc_rate
# 1 01 4.1 5.7 26800 25818 -3.664179
# 2 02 4.1 4.9 26838 26365 -1.762426
# 3 03 4.2 4.3 26609 26923 1.180052
# 4 04 4.2 4.0 26562 27214 2.454634
# 5 05 4.5 4.0 26930 27550 2.302265
# 6 06 4.3 3.8 27055 27637 2.151174
# 7 07 4.0 3.2 27106 27648 1.999557
# 8 08 3.1 2.6 27085 27603 1.912498
# 9 09 3.6 2.7 27012 27683 2.484081
# 10 10 3.7 2.8 27088 27741 2.410662
# 11 11 3.4 2.6 27241 27795 2.033699
# 12 12 4.1 3.5 26526 27298 2.910352
2. 실업률과 취업자 수 증가율 변수의 평균, 분산, 표준편차, 중앙값, 최대값, 최소값 계산
dplyr 패키지로 데이터의 요약통계량을 계산하는 방법은 https://rfriend.tistory.com/235 를 참고하세요.
여러개의 패키지별로 그룹별 요약통계량을 계산하는 방법은 https://rfriend.tistory.com/125 를 참고하세요.
## 2. 실업률과 취업자 수 증가율 변수의 평균, 분산, 표준편차, 중앙값, 최대값, 최소값 계산
df2 %>%
summarise(
unemploy_rate_2021_mean = mean(unemploy_rate_2021),
unemploy_rate_2021_var = var(unemploy_rate_2021),
unemploy_rate_2021_sd = sd(unemploy_rate_2021),
unemploy_rate_2021_median = median(unemploy_rate_2021),
unemploy_rate_2021_max = max(unemploy_rate_2021),
unemploy_rate_2021_min = min(unemploy_rate_2021)
)
# unemploy_rate_2021_mean unemploy_rate_2021_var unemploy_rate_2021_sd
# 3.675 0.9547727 0.9771247
#
# unemploy_rate_2021_median unemploy_rate_2021_max unemploy_rate_2021_min
# 3.65 5.7 2.6
df2 %>%
summarise(
employed_inc_rate_mean = mean(employed_inc_rate),
employed_inc_rate_var = var(employed_inc_rate),
employed_inc_rate_sd = sd(employed_inc_rate),
employed_inc_rate_median = median(employed_inc_rate),
employed_inc_rate_max = max(employed_inc_rate),
employed_inc_rate_min = min(employed_inc_rate)
)
# employed_inc_rate_mean employed_inc_rate_var employed_inc_rate_sd
# 1.367697 3.970439 1.992596
#
# employed_inc_rate_median employed_inc_rate_max employed_inc_rate_min
# 2.092436 2.910352 -3.664179
3. 실업률과 취업자 수 증가율 변수의 시계열 그래프 그리기
ggplot2 로 시계열 그래프 그리기는 https://rfriend.tistory.com/73 를 참고하세요.
## 3. 실업률과 취업자 수 증가율 변수의 시계열 그래프 그리기
library(ggplot2)
ggplot(df2, aes(x=month, y=unemploy_rate_2021, group=1)) +
geom_line() +
ylim(0, max(df2$unemploy_rate_2021)) +
ggtitle("Time Series Plot of Unemployment Rate, Year 2021")
ggplot(df2, aes(x=month, y=employed_inc_rate, group=1)) +
geom_line() +
ylim(min(df2$employed_inc_rate), max(df2$employed_inc_rate)) +
ggtitle("Time Series Plot of Employment Increase Rate, Year 2021")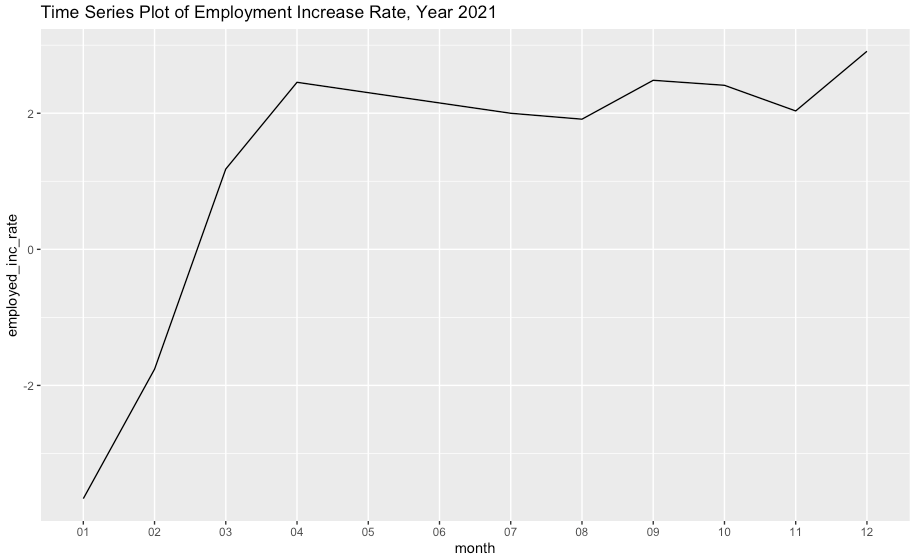
4. 실업률과 취업자 수 증가율 변수의 히스토그램 그리기 (히스토그램의 구간은 10개)
ggplot2 패키지로 히스토그램 그리기는 https://rfriend.tistory.com/67 를 참고하세요.
ggplot(df2, aes(x=employed_inc_rate)) +
geom_histogram(bins=10) +
ggtitle("Histogram of Unemployment Rate, Year 2021")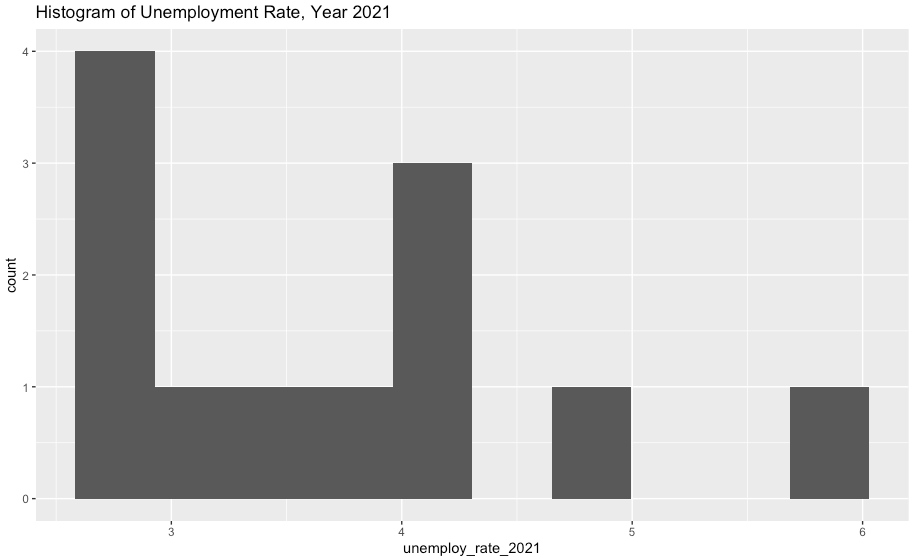
ggplot(df2, aes(x=employed_inc_rate)) +
geom_histogram(bins=10) +
ggtitle("Histogram of Employment Incease Rate, Year 2021")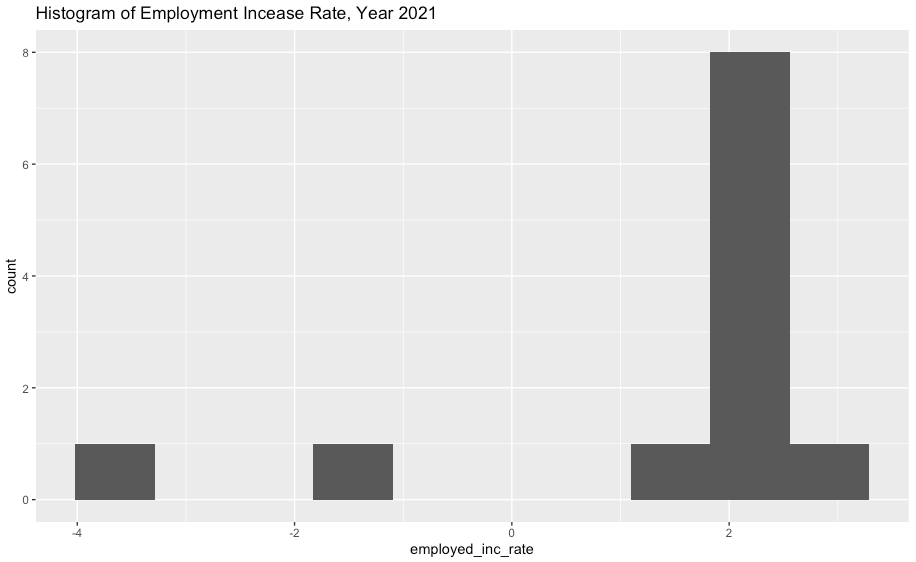
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)












