'R 분석과 프로그래밍' 카테고리의 글 목록 (7 Page)

[R] R 패키지 함수의 소스 코드를 볼 수 있는 방법 (how to see function's source codes in R package)

R 분석과 프로그래밍/R 데이터 전처리 2019. 10. 22. 22:01

R의 다양한 패키지들을 사용하다 보면 함수를 사용한 후의 산출물 결과가 자신이 생각했던 결과와 다를 경우 R 패키지 함수의 소스 코드가 어떻게 되어있는 것인지 궁금할 때가 있습니다.

이번 포스팅에서는 R 패키지에 있는 함수, 메소드의 소스 코드를 들여다볼 수 있는 2가지 방법을 소개하겠습니다.

(1) getAnywhere(function_name)

(2) package_name:::function_name

가령, 두 벡터의 차집합(difference of sets)을 구할 때 사용하는 함수가 base 패키지의 setdiff() 함수입니다.

> x <- c(1, 1, 2, 3, 4, 5)

> y <- c(4, 5, 6, 7)

> setdiff(x, y)

[1] 1 2 3

위에서 예로 든 base 패키지의 setdiff() 함수에 대한 소스 코드를 위의 2가지 방법을 사용해서 살펴보겠습니다.

(1) getAnywhere(function_name)

R package 의 이름을 몰라도 함수, 메소드의 이름만 알고 있으면 R package 이름과 namespace, 그리고 소스 코드를 친절하게 다 볼 수 있으므로 매우 편리합니다.

> getAnywhere(setdiff)

A single object matching ‘setdiff’ was found

It was found in the following places

package:base

namespace:base

with value

function (x, y)

{

x <- as.vector(x)

y <- as.vector(y)

unique(if (length(x) || length(y))

x[match(x, y, 0L) == 0L]

else x)

}

<bytecode: 0x000000000ff1e8d0>

<environment: namespace:base>

>

(2) R_package_name:::function_name

R package 이름을 알고 있다면 package_name:::function_name 의 형식으로 ':::' 를 사용해서 함수의 소스 코드를 들여다볼 수 있습니다. 위 (1)번의 getAnywhere() 함수가 기억이 잘 안날 때 쉽게 ':::' 를 사용해서 소스 코드 볼 때 편리합니다.

> base:::setdiff

function (x, y)

{

x <- as.vector(x)

y <- as.vector(y)

unique(if (length(x) || length(y))

x[match(x, y, 0L) == 0L]

else x)

}

<bytecode: 0x000000000ff1e8d0>

<environment: namespace:base>

많은 도움이 되었기를 바랍니다.

이번 포스팅이 도움이 되었다면 아래의 '공감~'를 꾹 눌러주세요. :-)

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] 여러개의 변수를 가진 DataFrame을 무작위 층화 샘플링으로 Train, Test set 분할하고 표준화하기 (0)	2020.01.19
[R] 장비 On, Off 상태로 가동 시간을 구하고, 장비 별 평균 가동 시간 구하기 (16)	2019.10.24
[R] 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고 내림차순 정렬하기 (16)	2019.10.15
[R] 원하는 R 패키지와 의존성 있는 R 패키지를 모두 한꺼번에 다운로드 하기 (tools::package_dependencies(), download.packages()) (4)	2019.04.27
[R] 그룹 별 행 합이 최대인 행만 선별하기 (Selecting rows which the RowSum is maximum per groups) (2)	2019.02.22

Posted by Rfriend

,

[R] 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고 내림차순 정렬하기

R 분석과 프로그래밍/R 데이터 전처리 2019. 10. 15. 23:25

이번 포스팅에서는 (1) 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고, (2) 각 패턴별로 발생 빈도 기준으로 내림차순 정렬하는 방법을 소개하겠습니다.

먼저 S = {1, 2, 3, 4, 5} 의 정수 집합에서 복원추출(replacement) 하여 무작위 샘플 1,000개를 생성해보겠습니다.

> #----------------------------------

> # counting and sorting by patterns

> #----------------------------------

>

> set.seed(123) # for reproducibility

>

> sample <- sample(x=1:5, size=1000, replace=TRUE)

> sample

[1] 2 4 3 5 5 1 3 5 3 3 5 3 4 3 1 5 2 1 2 5 5 4 4 5 4 4 3 3 2 1 5 5 4 4 1 3 4 2 2 2 1 3 3 2 1 1 2

[48] 3 2 5 1 3 4 1 3 2 1 4 5 2 4 1 2 2 5 3 5 5 4 3 4 4 4 1 3 2 2 4 2 1 2 4 3 4 1 3 5 5 5 1 1 4 2 4

[95] 2 1 4 1 3 3 3 2 3 5 3 5 5 4 3 1 5 2 1 5 4 1 3 5 3 3 4 2 2 2 2 5 1 1 1 4 4 5 4 4 3 4 5 4 5 3 2

[142] 3 1 1 5 2 2 1 2 4 5 3 2 2 1 2 3 2 3 2 3 2 4 2 2 3 4 2 3 2 4 1 5 4 4 4 2 3 5 3 5 2 4 2 3 3 2 3

[189] 5 5 2 2 5 4 5 3 3 4 1 3 2 5 4 3 3 5 2 2 1 1 3 2 2 4 1 4 2 3 5 5 2 5 4 4 1 2 3 3 4 5 4 3 3 1 2

[236] 2 1 5 1 5 3 4 1 4 2 4 2 5 5 4 2 2 3 2 3 4 1 3 3 5 5 5 4 5 3 3 2 2 1 3 5 1 1 1 4 4 5 3 1 4 4 1

[283] 2 2 1 2 1 2 1 4 2 1 1 5 4 5 5 1 1 4 4 1 4 4 4 3 1 1 3 3 2 3 4 1 2 5 5 2 2 5 5 2 1 4 1 1 5 1 2

[330] 5 4 2 4 5 2 3 4 4 4 5 3 1 3 2 3 2 5 2 2 4 1 5 3 1 4 5 4 3 2 5 1 1 5 2 2 4 1 1 3 3 3 2 5 3 3 5

[377] 4 2 2 5 3 4 2 4 3 5 1 2 1 2 5 2 4 4 1 2 2 1 1 5 5 1 5 3 2 3 4 1 2 4 2 5 2 3 2 1 5 2 3 1 3 4 3

[424] 2 5 4 2 2 1 5 5 3 2 5 2 4 1 3 1 1 2 3 4 1 5 4 4 1 2 4 3 2 2 1 2 5 5 4 1 1 5 3 3 1 3 2 2 4 2 5

[471] 1 5 3 4 4 3 4 1 2 4 2 5 2 4 5 1 1 4 3 5 5 1 3 4 1 5 2 1 4 4 2 2 2 1 2 1 3 3 5 2 3 1 5 2 4 1 3

[518] 4 1 5 2 2 2 1 3 4 5 1 5 2 5 4 3 5 1 4 2 5 3 2 5 1 5 2 4 5 1 5 5 2 2 2 3 5 3 3 4 3 3 1 1 5 4 2

[565] 4 4 2 5 3 5 3 5 3 3 5 4 3 1 3 3 5 5 5 2 5 1 2 4 5 3 3 1 5 1 1 5 3 2 5 1 2 4 2 2 1 5 1 5 2 2 4

[612] 1 1 5 3 4 5 4 5 1 5 5 4 2 1 2 2 5 2 2 4 5 3 4 1 2 5 4 5 3 3 4 5 2 1 4 4 1 2 4 4 5 3 3 4 5 5 1

[659] 3 2 5 5 1 4 2 1 5 1 4 1 1 3 1 2 3 3 5 2 3 3 4 4 5 5 5 3 3 1 3 2 1 4 3 1 2 3 1 1 3 2 5 2 1 5 2

[706] 4 3 2 1 3 4 3 4 4 3 2 1 1 5 1 3 4 4 5 4 4 5 4 4 1 3 5 4 5 1 2 5 5 2 1 5 1 1 3 2 3 4 1 4 5 2 2

[753] 1 1 3 3 3 5 1 2 3 2 3 3 3 1 1 3 4 4 5 5 4 5 1 2 2 3 4 5 2 5 1 4 5 3 2 1 2 5 5 3 2 3 5 3 1 2 2

[800] 2 3 2 1 1 2 5 3 3 4 4 1 4 2 5 4 1 2 1 3 3 4 2 4 5 4 1 3 1 2 4 1 4 3 4 4 3 4 4 2 1 5 4 4 1 3 2

[847] 5 1 2 1 2 4 5 4 3 3 5 1 1 5 3 1 4 3 4 2 1 1 3 3 1 1 4 3 5 4 1 4 5 4 1 5 4 1 4 5 3 2 2 2 3 4 4

[894] 3 5 4 1 2 1 4 5 3 5 3 4 3 4 5 5 1 1 1 5 3 2 5 3 3 2 2 5 1 2 5 4 4 2 3 1 4 5 2 4 3 5 1 3 5 5 1

[941] 5 3 2 3 1 1 3 2 3 2 3 1 5 1 2 5 4 1 3 3 3 3 4 1 5 3 3 1 4 3 4 1 5 2 2 4 5 1 2 3 3 4 5 4 5 4 1

[988] 1 1 3 1 2 3 3 3 5 4 2 4 1

다음으로 순차적으로 3개의 정수를 묶음으로 하여 1개씩 이동하면서 패턴을 정의하고(패턴1 {X1, X2, X3}, 패턴2 {X2, X3, X4}, ..., 패턴n-2 {Xn-2, Xn-1, X}, 위의 정수 난수 샘플을 가지고 예를 들면, 첫번째 3개 묶음의 패턴은 '2_4_3', 두번째 3개 묶음의 패턴은 '4_3_5', 세번째 3개 묶음의 패턴은 '3_5_5', ... ), 각 패턴별로 발생 빈도를 세어보겠습니다

먼저 비어있는 pattern_list 라는 이름의 리스트(list) 를 만들어놓구요,

for loop 반복문을 사용하여 '패턴1' {X1, X2, X3}, '패턴2' {X2, X3, X4}, ..., '패턴n-2' {Xn-2, Xn-1, X} 을 생성합니다.

if else 조건문을 사용하여, 만약 3개 정수 묶음의 패턴이 pattern_list의 키(key)에 이미 들어있는 것이면 +1 을 추가해주구요, 그렇지 않다면 (처음 발생하는 패턴이라면) pattern_list의 키(key)에 새로 발생한 패턴을 키로 추가해주고 값(value)으로 1을 부여해줍니다.

> # blank list to store the patterns' count

> pattern_list <- {}

>

> # count per patterns

> for (i in 1:(length(sample)-2)){

+

+ pattern <- paste(sample[i], sample[i+1], sample[i+2], sep="_")

+

+ if (pattern %in% names(pattern_list)) {

+ pattern_list[[pattern]] <- pattern_list[[pattern]] + 1

+ } else {

+ pattern_list[[pattern]] <- 1

+ }

>

> pattern_list

2_4_3 4_3_5 3_5_5 5_5_1 5_1_3 1_3_5 3_5_3 5_3_3 3_3_5 5_3_4 3_4_3 4_3_1 3_1_5 1_5_2 5_2_1 2_1_2

6 7 10 9 6 6 10 15 11 7 5 5 5 13 7 12

1_2_5 2_5_5 5_5_4 5_4_4 4_4_5 4_5_4 4_4_3 4_3_3 3_3_2 3_2_1 2_1_5 1_5_5 4_4_1 4_1_3 1_3_4 3_4_2

11 8 9 11 9 13 7 5 8 9 10 5 11 14 9 6

4_2_2 2_2_2 2_2_1 2_1_3 1_3_3 2_1_1 1_1_2 1_2_3 2_3_2 3_2_5 2_5_1 3_4_1 1_3_2 2_1_4 1_4_5 4_5_2

8 8 14 6 11 8 3 9 11 13 10 15 12 8 8 6

5_2_4 2_4_1 4_1_2 1_2_2 2_2_5 2_5_3 5_3_5 5_4_3 4_3_4 3_4_4 4_4_4 3_2_2 2_2_4 2_4_2 4_2_1 1_2_4

9 10 12 7 7 7 6 8 10 11 4 8 8 9 7 10

5_5_5 5_1_1 1_1_4 1_4_2 4_2_4 1_4_1 3_3_3 3_2_3 2_3_5 1_5_4 5_4_1 3_3_4 1_1_1 1_4_4 3_4_5 5_4_5

4 10 6 7 7 3 7 15 6 7 10 11 4 7 9 9

4_5_3 5_3_2 2_3_1 3_1_1 1_1_5 5_2_2 2_4_5 3_2_4 2_2_3 2_3_4 4_2_3 4_1_5 4_4_2 3_5_2 2_3_3 5_5_2

13 11 7 8 12 12 9 2 6 9 5 8 5 4 7 7

2_5_4 1_1_3 4_1_4 5_2_5 3_3_1 3_1_2 1_5_1 5_1_5 1_5_3 4_2_5 5_4_2 3_5_1 5_3_1 3_1_4 1_2_1 4_5_5

10 11 8 4 8 6 8 9 11 7 7 6 5 5 7 5

4_1_1 5_1_2 5_2_3 3_1_3 2_5_2 4_3_2 3_5_4 2_4_4 5_5_3 1_3_1 4_5_1 1_4_3 5_1_4

6 11 5 5 7 5 6 3 3 4 7 6 4

이제 발생 빈도를 기준으로 패턴 리스트를 내림차순 정렬(sort in descending order)을 해보겠습니다.

'5_3_3', '3_4_1', '3_2-3' 패턴이 총 15번 발생해서 공동 1등을 하였네요.

> # sorting pattern_list in descending order

>

> sort(pattern_list, decreasing = TRUE)

5_3_3 3_4_1 3_2_3 4_1_3 2_2_1 1_5_2 4_5_4 3_2_5 4_5_3 2_1_2 1_3_2 4_1_2 1_1_5 5_2_2 3_3_5 1_2_5

15 15 15 14 14 13 13 13 13 12 12 12 12 12 11 11

5_4_4 4_4_1 1_3_3 2_3_2 3_4_4 3_3_4 5_3_2 1_1_3 1_5_3 5_1_2 3_5_5 3_5_3 2_1_5 2_5_1 2_4_1 4_3_4

11 11 11 11 11 11 11 11 11 11 10 10 10 10 10 10

1_2_4 5_1_1 5_4_1 2_5_4 5_5_1 5_5_4 4_4_5 3_2_1 1_3_4 1_2_3 5_2_4 2_4_2 3_4_5 5_4_5 2_4_5 2_3_4

10 10 10 10 9 9 9 9 9 9 9 9 9 9 9 9

5_1_5 2_5_5 3_3_2 4_2_2 2_2_2 2_1_1 2_1_4 1_4_5 5_4_3 3_2_2 2_2_4 3_1_1 4_1_5 4_1_4 3_3_1 1_5_1

9 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8

4_3_5 5_3_4 5_2_1 4_4_3 1_2_2 2_2_5 2_5_3 4_2_1 1_4_2 4_2_4 3_3_3 1_5_4 1_4_4 2_3_1 2_3_3 5_5_2

7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7

4_2_5 5_4_2 1_2_1 2_5_2 4_5_1 2_4_3 5_1_3 1_3_5 3_4_2 2_1_3 4_5_2 5_3_5 1_1_4 2_3_5 2_2_3 3_1_2

7 7 7 7 7 6 6 6 6 6 6 6 6 6 6 6

3_5_1 4_1_1 3_5_4 1_4_3 3_4_3 4_3_1 3_1_5 4_3_3 1_5_5 4_2_3 4_4_2 5_3_1 3_1_4 4_5_5 5_2_3 3_1_3

6 6 6 6 5 5 5 5 5 5 5 5 5 5 5 5

4_3_2 4_4_4 5_5_5 1_1_1 3_5_2 5_2_5 1_3_1 5_1_4 1_1_2 1_4_1 2_4_4 5_5_3 3_2_4

5 4 4 4 4 4 4 4 3 3 3 3 2

위의 패턴별 발생 빈도수 기준으로 정렬된 결과를 DataFrame으로 변환해서 상위 10개 패턴을 프린트해보겠습니다.

> # convert a list to DataFrame

> cnt_per_pattern_sorted <- sort(pattern_list, decreasing = TRUE)

> pattern <- names(cnt_per_pattern_sorted)

> df <- data.frame(pattern, cnt_per_pattern_sorted)

> rownames(df) <- NULL

>

> # display top 10 patterns

> df[1:10,]

pattern cnt_per_pattern_sorted

1 5_3_3 15

2 3_4_1 15

3 3_2_3 15

4 4_1_3 14

5 2_2_1 14

6 1_5_2 13

7 4_5_4 13

8 3_2_5 13

9 4_5_3 13

10 2_1_2 12

많은 도움이 되었기를 바랍니다.

이번 포스팅이 도움이 되었다면 아래의 '공감~'를 꾹 눌러주세요. ^^

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] 장비 On, Off 상태로 가동 시간을 구하고, 장비 별 평균 가동 시간 구하기 (16)	2019.10.24
[R] R 패키지 함수의 소스 코드를 볼 수 있는 방법 (how to see function's source codes in R package) (0)	2019.10.22
[R] 원하는 R 패키지와 의존성 있는 R 패키지를 모두 한꺼번에 다운로드 하기 (tools::package_dependencies(), download.packages()) (4)	2019.04.27
[R] 그룹 별 행 합이 최대인 행만 선별하기 (Selecting rows which the RowSum is maximum per groups) (2)	2019.02.22
[R] 여러개의 데이터프레임을 리스트로 묶기 (how to combine many DataFrames into a List) : mget() (4)	2018.03.24

Posted by Rfriend

,

[R] ggplot2 의 커널 밀도 곡선(Kernel Density Curve)의 최대 피크값 좌표구하고 수직선 추가하기

R 분석과 프로그래밍/R 그래프_시각화 2019. 10. 3. 16:12

이번 포스팅에서는

(1) R ggplot2를 이용하여 커널 밀도 곡선(Kernel Density Curve)을 그리기,

(2) 커밀 밀도 곡선의 최대 피크값의 좌표 구하기
(X, Y coordinates of the peak value in kernel density curve)

(3) 커널 밀도 곡선의 최대 피크값 위치에 수직선을 추가하는 방법 (adding a vertical line at peak value in kernel density plot) 을 소개하겠습니다.

(1) R ggplot2로 커널 밀도 곡선 그리기 (Kernel Density Curve by R ggplot2)

예제로 사용할 데이터는 MASS 패키지에 내장되어 있는 Cars93 데이터프레임입니다. 자동차의 가격(Price 변수)에 대해서 R ggplot2로 커널 밀도 곡선 (not frequency, but density) 을 그려보겠습니다.

> library(MASS)

> library(ggplot2)

>

> ggplot(Cars93, aes(x=Price)) +

+ geom_density(fill = 'yellow') +

+ geom_line(stat = "density") +

+ expand_limits(y = 0) +

+ ggtitle("Kernel Density Curve")

(2) 커널 밀도 곡선의 최대 피크값의 좌표 구하기

(X, Y coordinates of the peak value in kernel density curve)

density(df$var) 함수를 사용하면 x 와 y 값의 요약통계량 (최소, Q1, 중앙값, Q3, 최대값)을 확인할 수 있습니다. y 값의 최대값(Max)은 5.025e-02 값이네요.

> density(Cars93$Price)

Call:

density.default(x = Cars93$Price)

Data: Cars93$Price (93 obs.); Bandwidth 'bw' = 3.011

x y

Min. :-1.634 Min. :1.608e-05

1st Qu.:16.508 1st Qu.:9.773e-04

Median :34.650 Median :5.329e-03

Mean :34.650 Mean :1.377e-02

3rd Qu.:52.792 3rd Qu.:2.078e-02

Max. :70.934 Max. :5.025e-02

이중에서 y 값 peak 값의 x 좌표를 알고 싶으므로 (a) which.max(density(Cars93$Price)$y) 로 y값의 최대 peak 값을 가지는 데이터의 index를 찾고 (127번째 데이터), 이 index를 이용해서 x 값의 좌표(16.25942)를 indexing 해올 수 있습니다.

> which.max(density(Cars93$Price)$y)

[1] 127

> x_coord_of_y_max = density(Cars93$Price)$x[127]

> x_coord_of_y_max

[1] 16.25942

즉, y (Price) 최대 피크값의 좌표는 (x, y) 는 (16.25922, 0.05025) 가 되겠습니다.

(3) 커널 밀도 곡선의 최대 피크값 위치에 수직선을 추가하기

(adding a vertical line at peak value in kernel density plot)

geom_vline() 으로 (2)번에서 구한 y 피크값의 x 좌표를 입력해주면 커널밀도곡선의 최대 피크값 위치에 수직선(vertical line)을 추가할 수 있습니다.

> ggplot(Cars93, aes(x=Price)) +

+ geom_density(fill = 'yellow') +

+ geom_line(stat = "density") +

+ expand_limits(y = 0) +

+ ggtitle("Kernel Density Curve w/ Vertical Line at Peak Point") +

+ geom_vline(xintercept = x_coord_of_y_max, color='blue', size=2, linetype="dotted")

(4) 여러개 그룹의 커널 밀도 곡선을 겹쳐 그린 경우 최대 peak 값 찾고 수직선 그리기

위의 예는 1개의 데이터셋에 대해 1개의 커널 밀도 곡선을 그린 후 최대 peak 값을 찾는 것이었습니다. 이제부터는 여러개의 하위 그룹으로 나뉘어진 데이터셋으로 여러개의 커널 밀도 곡선을 겹쳐서 그린 경우에 최대 peak 값을 찾고, 그 위치에 빨간색으로 수직선을 추가해보겠습니다.

예제로 Cars93 데이터프레임에서 차종(Type) 별 가격(Price)의 커널 밀도 곡선을 겹쳐서 그려보겠습니다.

> ggplot(Cars93, aes(x=Price, colour = Type)) +

+ geom_density(fill = NA) +

+ geom_line(stat = "density") +

+ expand_limits(y = 0) +

+ ggtitle("Kernel Density Curve by Car Types")

차종(Type) 중에서 Van 의 커널 밀도 곡선이 최대 Peak 값에 해당하므로 --> 차종 중에서 Van 의 데이터만 가져와서 y 최대값과 이에 해당하는 관측치의 index 위치를 찾아보겠습니다.

> density(Cars93[Cars93$Type=='Van', ]$Price)

Call:

density.default(x = Cars93[Cars93$Type == "Van", ]$Price)

Data: Cars93[Cars93$Type == "Van", ]$Price (9 obs.); Bandwidth 'bw' = 0.303

x y

Min. :15.39 Min. :0.0000072

1st Qu.:17.45 1st Qu.:0.0040424

Median :19.50 Median :0.0495649

Mean :19.50 Mean :0.1215343

3rd Qu.:21.55 3rd Qu.:0.1807290

Max. :23.61 Max. :0.5321582

> which.max(density(Cars93[Cars93$Type=='Van', 'Price'])$y)

[1] 238

> x_coord_of_y_max = density(Cars93[Cars93$Type=='Van','Price'])$x[238]

> x_coord_of_y_max

[1] 19.20249

밀도 y의 최대값(max)은 0.532 이며, 이때의 관측치의 index는 238번째 값 이고, 관측치 238번째 값의 x값의 좌표는 19.20 입니다.

따라서, 밀도 y 의 최대 peak 값의 좌표는 (x, y) = (19.20, 0.53) 이네요.

마지막으로, geom_vline() 을 사용해서 밀도 최대 peak 값에 해당하는 x=19.20 을 기준으로 빨간색 점선 수직선(vertical line)을 추가해보겠습니다.

> ggplot(Cars93, aes(x=Price, colour = Type)) +

+ geom_density(fill = NA) +

+ geom_line(stat = "density") +

+ expand_limits(y = 0) +

+ ggtitle("Kernel Density Curve w/ Vertical Line at Peak Point") +

+ theme_bw() +

+ geom_vline(xintercept = x_coord_of_y_max, color='red', size=1, linetype="dashed")

R ggplot2로 히스토그램, 커널밀도곡선을 그리는 다양한 방법은 https://rfriend.tistory.com/67 를 참고하세요.

많은 도움이 되었기를 바랍니다.

이번 포스팅이 도움이 되었다면 아래의 '공감~'를 꾹 눌러주세요. ^^

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 그래프_시각화' 카테고리의 다른 글

[R] 반복문 프로그램 진행 경과 막대로 나타내기 (progress bar) (1)	2021.01.23
[R] ggplot2로 bin 범위가 다른 히스토그램 그리기 (histogram with different bin width using R ggplot2) (4)	2019.02.17
[R] ggplot으로 이중축 그래프 그래기 (dual y-axes plot using ggplot2) (4)	2018.06.16
클리브랜드 점 그래프 (KRUG 2017.11.18 주말 퀴즈) (2)	2017.11.18
[R] ggplot 그래프 크기 조정, 가로 세로 비율 조정 : coord_fixed(ratio = 2, 1, 0.5) (0)	2017.09.09

Posted by Rfriend

,

[R] DataFrame에서 특정 조건에 해당하는 행과 앞, 뒤 2개 행을 같이 제거하는 방법

R 분석과 프로그래밍/R 프로그래밍 2019. 9. 27. 22:10

이번 포스팅에서는 R의 DataFrame에서 특정 조건에 해당하는 값의 행과, 해당 행의 앞, 뒤 2개 행(above and below 2 rows) 을 동시에 제거하는 방법을 소개하겠습니다.

예를 들어서, 아래와 같이 var1, var2의 두 개의 변수를 가지는 df라는 이름의 DataFrame이 있다고 했을 때, var2의 값 중 음수(-)인 값을 가지는 행과, 해당 행의 위, 아래 2개 행을 같이 제거(remove, filter) 해서 df2 라는 이름의 새로운 DataFrame을 만들어보겠습니다.

> var1 <- c(1:12)

> var2 <- c(100, -200, 101, 1102, 50, 300, 100, 400, -100, 82, 90, 80)

>

> df <- data.frame(var1, var2)

> df

var1 var2

1 1 100

2 2 -200

3 3 101

4 4 1102

5 5 50

6 6 300

7 7 100

8 8 400

9 9 -100

10 10 82

11 11 90

12 12 80

먼저, 칼럼 var2 에서 음수(-)인 값의 조건을 만족하는 값의 행의 위치를 indexing 한 negative_idx 벡터를 만들어보겠습니다.

> # condition: if var2 value is negative, then TRUE

> negative_idx <- df$var2 < 0

> negative_idx

[1] FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE

>

다음으로 칼럼 var2의 값이 음수(-)인 값의 위치를 기준으로 해당 값의 행과 앞, 뒤 2개행까지는 제거(remove, filter)하고, 그 외의 값은 유지(keep_idx = TRUE) 하는 keep_idx 라는 벡터를 for loop 반복문과 if 조건문을 사용해서 만들어보겠습니다.

> keep_idx <- c(rep(TRUE, length(df$var2)))

> keep_idx

[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

>

> for (i in 1:length(negative_idx)) {

+ if (negative_idx[i] == TRUE) {

+ keep_idx[i-2] = FALSE

+ keep_idx[i-1] = FALSE

+ keep_idx[i] = FALSE

+ keep_idx[i+1] = FALSE

+ keep_idx[i+2] = FALSE

+ }

>

> keep_idx

[1] FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE FALSE TRUE

이제 df라는 DataFrame에서 위에서 구한 keep_idx = TRUE 인 행만 indexing 해서 (즉, keep_idx = FALSE 인 행은 제거) 새로운 df2 라는 DataFrame을 만들어보겠습니다.

> # subset only rows with keep_idx = TRUE

> df_filstered <- df[keep_idx, ]

> df_filstered

var1 var2

5 5 50

6 6 300

12 12 80

위는 예는 조건문과 반복문을 사용해서 indexing 해오는 방법이었구요, windows 함수인 lag(), lead()를 사용해서도 동일한 기능을 수행하는 프로그램을 짤 수도 있습니다. 다만, 이번 포스팅에서 소개한 코드가 좀더 범용적이고 코드도 짧기 때문에 lag(), lead() 함수를 사용한 방법은 추가 설명은 하지 않겠습니다.

많은 도움이 되었기를 바랍니다.

이번 포스팅이 도움이 되었다면 아래의 '공감~'를 꾹 눌러주세요.

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 프로그래밍' 카테고리의 다른 글

[R] 웹사이트에서 텍스트를 가져다가 최저가 Top 10 리스트를 엑셀로 내보내기 (3)	2018.08.06
[R 프로그래밍] 반복문과 조건문을 써서 벡터에서 0이 연속 3번 나오면 구간 나누기 (6)	2018.02.02
[R] 데이터프레임 다수 item을 가진 문자형 변수를 분리 후에 세로로 재구조화하기 (11)	2016.09.29
[R] 여러개의 데이터프레임을 한꺼번에 하나의 데이터프레임으로 묶기, data.table package : rbindlist(data) (8)	2016.07.10
[R] 폴더 내 여러개 파일들을 Loop 돌려서 자동으로 불러오기 (154)	2016.07.02

Posted by Rfriend

,

수식 표기를 영어로 읽는 방법 (how to read mathematical notation in English)

R 분석과 프로그래밍/R 기계학습 2019. 9. 14. 22:24

이번 포스팅에서는 수식 표기(mathematical notation)를 영어로 어떻게 읽는지 정리한 표를 소개하겠습니다.

통계, 기계학습, 딥러닝 공부할 때 수식이 나올 때면 '이걸 어떻게 읽어야 하나?'하고 궁금했던 적이 있을 것입니다. 한글로 된 책을 읽거나 강의를 들을 때면 '저렇게 읽는게 맞나? 저렇게 읽은 것을 듣고서 거꾸로 수식으로 정확하게 옮길 수 있나?' 하는 의문을 가진 적도 있을 것이구요.

수식을 영어로 읽는 법을 알고 있으면 많은 도움이 되겠다는 생각에 한번은 정리를 해봐야지...하고 미루고 있던 차에요, 'Deep Learning' (by Ian Goodfellow, Yoshua Bengio, and Aaron Courville, The MIT Press) 책에서 깔끔하게 정리된 자료를 찾았습니다.

1. 수와 배열 (Numbers and Arrays)

2. 집합과 그래프 (Sets and Graphs)

3. 인덱싱 (Indexing)

4. 선형대수 연산 (Linear Algebra Operations)

5. 미적분 (Calculus)

6. 확률과 정보 이론 (Probability and Information Theory)

7. 함수 (Functions)

8. 데이터셋과 분포 (Datasets and Distributions)

* source: 'Deep Learning' (by Ian Goodfellow, Yoshua Bengio, and Aaron Courville, The MIT Press)

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 기계학습' 카테고리의 다른 글

[R] 다변량 정규분포 확률밀도함수(multivariate normal distribution probability density function) (2)	2016.09.04
[R 기계학습] 과적합(Over-fitting), Bias-Variance Trade-off (Delimma) (9)	2016.05.14
[R 기계학습] 과적합(Over-fitting)을 피할 수 있는 방법은? (Training vs. Validation vs. Test set) (40)	2016.05.05
[R 기계학습] 과적합(Over-fitting) 이란 무엇인가? (0)	2016.05.04
[R 기계학습] 기계학습이란? 기계학습의 유형/알고리즘 종류? (15)	2016.05.01

Posted by Rfriend

,

[R] R Shiny 로 두 집단 간 평균 차이 t-검정(t-Test) 신뢰수준별 신뢰구간 구하는 웹 애플리케이션 만들기

R 분석과 프로그래밍/R 동적 문서(Dynamic Document) 2019. 6. 30. 22:26

이번 포스팅에서는 R Shiny를 사용하여

- (1) 두 개의 독립 표본 집단 간 평균 차이 t-검정 (independent two-sample t-test)

- (2) 신뢰수준 별 신뢰구간 (confidence interval by confidence level)

을 구하는 웹 애플리케이션을 만들어보겠습니다.

예제로 사용한 데이터는 MASS 패키지의 Cars93 데이터프레임이며, 'Origin' 변수의 두 개 집단(USA, Non-USA) 별로 Price, RPM, Length, Width 변수 간의 t-test 를 해보겠습니다.

왼쪽 사이드바 패널에는 t-검정을 할 변수를 선택할 수 있는 콤보 박스와, 신뢰수준(confidence level)을 지정할 수 있는 슬라이드 입력(default = 0.95) 화면을 만들었습니다.

그리고 메인 패널에는 변수 이름, 신뢰수준, t-검정 결과를 텍스트로 보여줍니다.

library(shiny)

# Define UI for application that does t-test

ui <- fluidPage(

# Application title

titlePanel("Independent two sample t-test"),

# Select a variable to do t-test by Origin (USA vs. non-USA groups)

sidebarPanel(

selectInput("var_x",

label = "Select a Variable to do t-test",

choices = list("Price"="Price",

"RPM"="RPM",

"Length"="Length",

"Width"="Width"),

selected = "Price"),

sliderInput("conf_level", "Confidence Level:",

min = 0.05, max = 0.99, value = 0.95)

),

# Show a t-test result

mainPanel(

h5("Variable is:"),

verbatimTextOutput("var_x_name"),

h5("Confidence Level is:"),

verbatimTextOutput("conf_level"),

h4("t-test Result by Origin (USA vs. non-USA independent two samples)"),

verbatimTextOutput("t_test")

)

# Define server logic required to do t-test

server <- function(input, output) {

library(MASS)

cars93_sub <- Cars93[, c('Origin', 'Price', 'RPM', 'Length', 'Width')]

output$var_x_name <- renderText({

as.character(input$var_x)

})

output$conf_level <- renderText({

as.character(input$conf_level)

})

output$t_test <- renderPrint({

# independent two-sample t-test

t.test(cars93_sub[,input$var_x] ~ Origin,

data = cars93_sub,

alternative = c("two.sided"),

var.equal = FALSE,

conf.level = input$conf_level)

})

}

# Run the application

shinyApp(ui = ui, server = server)

많은 도움이 되었기를 바랍니다.

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] R Shiny로 두 연속형 변수 간 상관계수, 산점도와 회귀선 그리는 앱 애플리케이션 만들기 (2)	2019.06.30
[R] R Shiny로 연속형 변수 별 요약 통계량 조회하는 Interactive App 만들기 (0)	2019.06.29
[R] rmarkdown HTML 문서의 포맷 정하기 (7)	2017.05.02
[R] servr 패키지를 사용해서 .Rmd 파일들을 자동 rendering 하고 로컬 웹 서버로 올리기 (0)	2017.05.01
[R] RStudio 를 사용해서 HTML 문서 만들기 (2)	2017.04.30

Posted by Rfriend

,

[R] R Shiny로 두 연속형 변수 간 상관계수, 산점도와 회귀선 그리는 앱 애플리케이션 만들기

R 분석과 프로그래밍/R 동적 문서(Dynamic Document) 2019. 6. 30. 22:07

이번 포스팅에서는 R Shiny를 사용하여 interactive하게 편하고 쉽게 두 연속형 변수 간 관계를 알아볼 수 있도록

(1) 상관계수 (Correlation Coefficient)를 구하고,

(2) 산점도 (Scatter Plot)을 그린 후,

(3) 선형 회귀선 (Linear Regression Line) 을 겹쳐서 그려주는

웹 애플리케이션을 만들어보겠습니다.

R Shiny - Correlation Coefficient, Scatter Plot, Linear Regression Line

예제로 사용할 데이터는 MASS 패키지에 내장되어 있는 Cars93 데이터프레임으로서, Price, MPG.city, MPG.highway, EngineSize, Horsepower, RPM 의 6개 연속형 변수를 선별하였습니다.

왼쪽 사이드바 패널에는 산점도의 X축, Y축에 해당하는 연속형 변수를 콤보박스로 선택할 수 있도록 하였으며, 상관계수와 선형회귀모형을 적합할 지 여부를 선택할 수 있는 체크박스도 추가하였습니다.

오른쪽 본문의 메인 패널에는 두 연속형 변수에 대한 산점도 그래프에 선형 회귀선을 겹쳐서 그려서 보여주고, 상관계수와 선형회귀 적합 결과를 텍스트로 볼 수 있도록 화면을 구성하였습니다.

library(shiny)

# Define UI for application that analyze correlation coefficients and regression

ui <- fluidPage(

# Application title

titlePanel("Correlation Coefficients and Regression"),

# Select 2 Variables, X and Y

sidebarPanel(

selectInput("var_x",

label = "Select a Variable of X",

choices = list("Price"="Price",

"MPG.city"="MPG.city",

"MPG.highway"="MPG.highway",

"EngineSize"="EngineSize",

"Horsepower"="Horsepower",

"RPM"="RPM"),

selected = "RPM"),

selectInput("var_y",

label = "Select a Variable of Y",

choices = list("Price"="Price",

"MPG.city"="MPG.city",

"MPG.highway"="MPG.highway",

"EngineSize"="EngineSize",

"Horsepower"="Horsepower",

"RPM"="RPM"),

selected = "MPG.highway"),

checkboxInput(inputId = "corr_checked",

label = strong("Correlation Coefficients"),

value = TRUE),

checkboxInput(inputId = "reg_checked",

label = strong("Simple Regression"),

value = TRUE)

),

# Show a plot of the generated distribution

mainPanel(

h4("Scatter Plot"),

plotOutput("scatterPlot"),

h4("Correlation Coefficent"),

verbatimTextOutput("corr_coef"),

h4("Simple Regression"),

verbatimTextOutput("reg_fit")

)

# Define server logic required to analyze correlation coefficients and regression

server <- function(input, output) {

library(MASS)

scatter <- Cars93[,c("Price", "MPG.city", "MPG.highway", "EngineSize", "Horsepower", "RPM")]

# scatter plot

output$scatterPlot <- renderPlot({

var_name_x <- as.character(input$var_x)

var_name_y <- as.character(input$var_y)

plot(scatter[, input$var_x],

scatter[, input$var_y],

xlab = var_name_x,

ylab = var_name_y,

main = "Scatter Plot")

# add linear regression line

fit <- lm(scatter[, input$var_y] ~ scatter[, input$var_x])

abline(fit)

})

# correlation coefficient

output$corr_coef <- renderText({

if(input$corr_checked){

cor(scatter[, input$var_x],

scatter[, input$var_y])

}

})

# simple regression

output$reg_fit <- renderPrint({

if(input$reg_checked){

fit <- lm(scatter[, input$var_y] ~ scatter[, input$var_x])

names(fit$coefficients) <- c("Intercept", input$var_x)

summary(fit)$coefficients

}

})

}

# Run the application

shinyApp(ui = ui, server = server)

많은 도움이 되었기를 바랍니다.

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] R Shiny 로 두 집단 간 평균 차이 t-검정(t-Test) 신뢰수준별 신뢰구간 구하는 웹 애플리케이션 만들기 (5)	2019.06.30
[R] R Shiny로 연속형 변수 별 요약 통계량 조회하는 Interactive App 만들기 (0)	2019.06.29
[R] rmarkdown HTML 문서의 포맷 정하기 (7)	2017.05.02
[R] servr 패키지를 사용해서 .Rmd 파일들을 자동 rendering 하고 로컬 웹 서버로 올리기 (0)	2017.05.01
[R] RStudio 를 사용해서 HTML 문서 만들기 (2)	2017.04.30

Posted by Rfriend

,

[R] R Shiny로 연속형 변수 별 요약 통계량 조회하는 Interactive App 만들기

R 분석과 프로그래밍/R 동적 문서(Dynamic Document) 2019. 6. 29. 23:55

R Shiny를 이용하면 탐색적 데이터 분석(Exploratory Data Analysis)을 할 때 요약 통계량, 그래프를 변수, 기간, 통계량, 그래프 종류 등을 자유롭게 조건 선택하고 조합하여 편리하게 사용할 수 있습니다.

이번 포스팅에서는 R Shiny로 DataFrame 의

(1) 특정 연속형 변수를 선택하고

(2) 분석하고 싶은 요약 통계량을 선택했을 때

(3) 요약 통계량 결과를 interactive하게 볼 수 있는 웹 애플리케이션을 만들어보겠습니다.

Output Image는 아래와 같습니다.

[ R Shiny 를 활용한 연속형 변수 요약 통계량 조회 웹 애플리케이션 화면 ]

먼저 R Studio 에서 'File > New File > Shiny Web App' 을 선택해주세요.

다음으로, (a) 애플리케이션의 이름, (b) 애플리케이션 유형 (간단한 것이면 하나의 파일에 UI와 Server를 함께 만드는게 편하구요, 복잡한 것이면 ui.R, server.R 의 두 개의 파일로 분리하는 것이 편리함), (c) 애플리케이션 저장 경로 (위치)를 지정해주고, Create 해줍니다.

이제 R Shiny 코드를 짜볼 텐데요,

먼저 UI 부분에서는 (a) 왼쪽 사이드바에서 분석 대상이 되는 변수를 콤보 박스로 선택하는 화면, (b) 왼쪽 사이드바에서 요약 통계량을 선택하는 체크 박스 화면, (c) 중앙 메인 패널에서 보여줄 제목과 요약 통계량 테이블을 지정해줍니다.

그리고 Server 부분에서는 (a) MASS 패키지의 Cars93 데이터 프레임으로 부터 일부 6개의 연속형 변수 데이터 읽어오기, (b) 요약 통계량 계산하기 (단, 결측값은 제외하기), (c) 요약 통계량들을 하나의 데이터 프레임으로 만들기, (d) 데이터 프레임 테이블을 렌더링 해줍니다.

#------------------------------------------------------------------
# Summary Statistics of a Continuous Variable using RShiny
#------------------------------------------------------------------

library(shiny)

# Define UI for application that calculate summary statistics
ui <- fluidPage(

   # Application title
   titlePanel("Descriptive Statistics of Automobiles"),

   # select Input from lists
   sidebarPanel(
     selectInput("var", "Select a Variable to Analyze",
                 choice = c("Price"=1,
                            "MPG.city"=2,
                            "MPG.highway"=3,
                            "EngineSize"=4,
                            "Horsepower"=5,
                            "RPM"=6),
                 selectize = F),

     checkboxGroupInput("checked", "Check summary statistics",
                        list(mean = "mean",
                             std_dev = "std_dev",
                             median = "median",
                             min = "min",
                             max = "max",
                             obs_num = "obs_num",
                             quartile_1 = "quartile_1",
                             quartile_3 = "quartile_3"),
                        selected = "mean")
   ),
   mainPanel(
     h4("Summary Statistics of a variable"),
     tableOutput("desc_statistics")
   )
)

# Define server logic required to calculate summary statistics
server <- function(input, output) {
  # read dataset
  library(MASS)
  descriptive <- Cars93[,c("Price", "MPG.city", "MPG.highway", "EngineSize", "Horsepower", "RPM")]

  output$desc_statistics <- renderTable({
    # summary statistics
    variable <- colnames(descriptive)[as.numeric(input$var)]
    mean <- mean(descriptive[, as.numeric(input$var)], na.rm=TRUE)
    std_dev <- sd(descriptive[, as.numeric(input$var)], na.rm=TRUE)
    median <- median(descriptive[, as.numeric(input$var)], na.rm=TRUE)
    min <- min(descriptive[, as.numeric(input$var)], na.rm=TRUE)
    max <- max(descriptive[, as.numeric(input$var)], na.rm=TRUE)
    obs_num <- nrow(descriptive)
    quartile_1 <- quantile(descriptive[, as.numeric(input$var)], 0.25, na.rm=TRUE)
    quartile_3 <- quantile(descriptive[, as.numeric(input$var)], 0.75, na.rm=TRUE)

    # make a DataFrame
    desc_summary <- data.frame(variable,
                               mean, std_dev,
                               median, min, max,
                               obs_num,
                               quartile_1, quartile_3)

    # render Table
    desc_summary[, c("variable", input$checked), drop = FALSE]
  })
}

# Run the application
shinyApp(ui = ui, server = server)

마지막으로, shinyApp(ui = ui, server = server) 로 UI와 Server를 지정해주고, 저장한 후에, RStudio 우측 상단의 'Run App' 단추를 눌러서 실행시켜주면 됩니다.

많은 도움이 되었기를 바랍니다.

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] R Shiny 로 두 집단 간 평균 차이 t-검정(t-Test) 신뢰수준별 신뢰구간 구하는 웹 애플리케이션 만들기 (5)	2019.06.30
[R] R Shiny로 두 연속형 변수 간 상관계수, 산점도와 회귀선 그리는 앱 애플리케이션 만들기 (2)	2019.06.30
[R] rmarkdown HTML 문서의 포맷 정하기 (7)	2017.05.02
[R] servr 패키지를 사용해서 .Rmd 파일들을 자동 rendering 하고 로컬 웹 서버로 올리기 (0)	2017.05.01
[R] RStudio 를 사용해서 HTML 문서 만들기 (2)	2017.04.30

Posted by Rfriend

,

[R] 원하는 R 패키지와 의존성 있는 R 패키지를 모두 한꺼번에 다운로드 하기 (tools::package_dependencies(), download.packages())

R 분석과 프로그래밍/R 데이터 전처리 2019. 4. 27. 22:32

회사의 보안 정책 상 사내 폐쇄망으로 운영함에 따라 R 패키지를 인터넷으로부터 바로 다운로드하지 못하는 경우가 있습니다. 이처럼 폐쇄망일 경우 R 패키지를 설치하는 것이 '지옥 그 자체!' 일 수 있습니다. 왜냐하면 특정 R 패키지를 설치하려면 그와 의존성이 있는 다른 패키지를 설치해야만 하고, 그 의존성이 있는 패키지는 또 다른 의존성이 있는 패키지가 설치되어야만 하고.... 꼬리에 꼬리를 무는 의존성 있는 패키지들을 설치하다보면 입에서 투덜거림이 궁시렁 궁시렁 나오게 됩니다. -_-;;;

이럴 때 편리하게 사용할 수 있는 'R 패키지 다운로드 & 의존성 있는 R 패키지도 같이 한꺼번에 다운로드 하기' 하는 방법을 소개하겠습니다.

먼저 R 패키지를 다운로드 받아 놓을 'r-pkt' 폴더를 만들어보겠습니다.

> mainDir <- "/Users/ihongdon/Downloads"

> subDir <- "r-pkg"

> dir.create(file.path(mainDir, subDir), showWarnings = FALSE)

다음으로 tools 패키지의 package_dependencies() 함수를 이용하여 다운도르하려는 특정 R 패키지와 이 패키지의 의존성 있는 패키지(dependencies of package)들 정보를 가져오는 사용자 정의 함수 getPackages() 를 만들어보겠습니다.

# UDF for get packages with dependencies

getPackages <- function(packs){

packages <- unlist(

# Find (recursively) dependencies or reverse dependencies of packages.

tools::package_dependencies(packs, available.packages(),

which=c("Depends", "Imports"), recursive=TRUE)

)

packages <- union(packs, packages)

return(packages)

}

자, 이제 준비가 되었으니 예제로 "dplyr"와 "ggplot2" 의 두 개 패키지와 이들과 의존성을 가지는 패키지들을 getPackages() 사용자 정의 함수로 정보를 가져온 후에, download.packages() 함수로 '/Users/ihongdon/Downloads/r-pkg' 폴더로 다운로드 해보도록 하겠습니다.

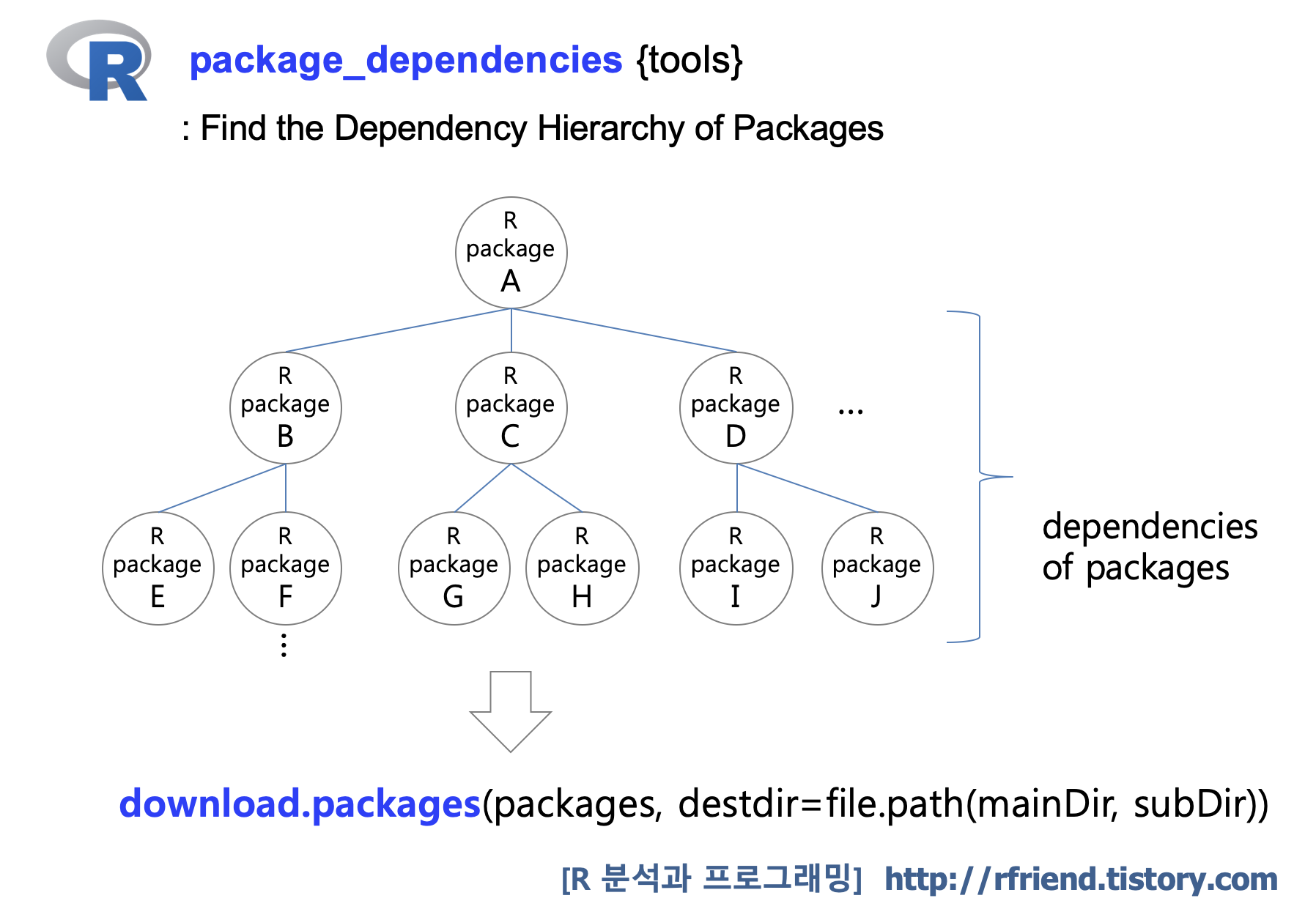
> packages <- getPackages(c("dplyr", "ggplot2"))

> download.packages(packages, destdir=file.path(mainDir, subDir))

trying URL 'https://cran.rstudio.com/src/contrib/dplyr_0.8.0.1.tar.gz'

Content type 'application/x-gzip' length 1075146 bytes (1.0 MB)

==================================================

downloaded 1.0 MB

trying URL 'https://cran.rstudio.com/src/contrib/ggplot2_3.1.1.tar.gz'

Content type 'application/x-gzip' length 2862022 bytes (2.7 MB)

==================================================

downloaded 2.7 MB

trying URL 'https://cran.rstudio.com/src/contrib/assertthat_0.2.1.tar.gz'

Content type 'application/x-gzip' length 12742 bytes (12 KB)

==================================================

downloaded 12 KB

trying URL 'https://cran.rstudio.com/src/contrib/glue_1.3.1.tar.gz'

Content type 'application/x-gzip' length 122950 bytes (120 KB)

==================================================

downloaded 120 KB

trying URL 'https://cran.rstudio.com/src/contrib/magrittr_1.5.tar.gz'

Content type 'application/x-gzip' length 200504 bytes (195 KB)

==================================================

downloaded 195 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'methods' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/pkgconfig_2.0.2.tar.gz'

Content type 'application/x-gzip' length 6024 bytes

==================================================

downloaded 6024 bytes

trying URL 'https://cran.rstudio.com/src/contrib/R6_2.4.0.tar.gz'

Content type 'application/x-gzip' length 31545 bytes (30 KB)

==================================================

downloaded 30 KB

trying URL 'https://cran.rstudio.com/src/contrib/Rcpp_1.0.1.tar.gz'

Content type 'application/x-gzip' length 3661123 bytes (3.5 MB)

==================================================

downloaded 3.5 MB

trying URL 'https://cran.rstudio.com/src/contrib/rlang_0.3.4.tar.gz'

Content type 'application/x-gzip' length 858992 bytes (838 KB)

==================================================

downloaded 838 KB

trying URL 'https://cran.rstudio.com/src/contrib/tibble_2.1.1.tar.gz'

Content type 'application/x-gzip' length 311836 bytes (304 KB)

==================================================

downloaded 304 KB

trying URL 'https://cran.rstudio.com/src/contrib/tidyselect_0.2.5.tar.gz'

Content type 'application/x-gzip' length 21883 bytes (21 KB)

==================================================

downloaded 21 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'utils' at the repositories

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'tools' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/cli_1.1.0.tar.gz'

Content type 'application/x-gzip' length 40232 bytes (39 KB)

==================================================

downloaded 39 KB

trying URL 'https://cran.rstudio.com/src/contrib/crayon_1.3.4.tar.gz'

Content type 'application/x-gzip' length 658694 bytes (643 KB)

==================================================

downloaded 643 KB

trying URL 'https://cran.rstudio.com/src/contrib/fansi_0.4.0.tar.gz'

Content type 'application/x-gzip' length 266123 bytes (259 KB)

==================================================

downloaded 259 KB

trying URL 'https://cran.rstudio.com/src/contrib/pillar_1.3.1.tar.gz'

Content type 'application/x-gzip' length 103972 bytes (101 KB)

==================================================

downloaded 101 KB

trying URL 'https://cran.rstudio.com/src/contrib/purrr_0.3.2.tar.gz'

Content type 'application/x-gzip' length 373701 bytes (364 KB)

==================================================

downloaded 364 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'grDevices' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/utf8_1.1.4.tar.gz'

Content type 'application/x-gzip' length 218882 bytes (213 KB)

==================================================

downloaded 213 KB

trying URL 'https://cran.rstudio.com/src/contrib/digest_0.6.18.tar.gz'

Content type 'application/x-gzip' length 128553 bytes (125 KB)

==================================================

downloaded 125 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'grid' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/gtable_0.3.0.tar.gz'

Content type 'application/x-gzip' length 368081 bytes (359 KB)

==================================================

downloaded 359 KB

trying URL 'https://cran.rstudio.com/src/contrib/lazyeval_0.2.2.tar.gz'

Content type 'application/x-gzip' length 83482 bytes (81 KB)

==================================================

downloaded 81 KB

trying URL 'https://cran.rstudio.com/src/contrib/MASS_7.3-51.4.tar.gz'

Content type 'application/x-gzip' length 487233 bytes (475 KB)

==================================================

downloaded 475 KB

trying URL 'https://cran.rstudio.com/src/contrib/mgcv_1.8-28.tar.gz'

Content type 'application/x-gzip' length 915991 bytes (894 KB)

==================================================

downloaded 894 KB

trying URL 'https://cran.rstudio.com/src/contrib/plyr_1.8.4.tar.gz'

Content type 'application/x-gzip' length 392451 bytes (383 KB)

==================================================

downloaded 383 KB

trying URL 'https://cran.rstudio.com/src/contrib/reshape2_1.4.3.tar.gz'

Content type 'application/x-gzip' length 36405 bytes (35 KB)

==================================================

downloaded 35 KB

trying URL 'https://cran.rstudio.com/src/contrib/scales_1.0.0.tar.gz'

Content type 'application/x-gzip' length 299262 bytes (292 KB)

==================================================

downloaded 292 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'stats' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/viridisLite_0.3.0.tar.gz'

Content type 'application/x-gzip' length 44019 bytes (42 KB)

==================================================

downloaded 42 KB

trying URL 'https://cran.rstudio.com/src/contrib/withr_2.1.2.tar.gz'

Content type 'application/x-gzip' length 53578 bytes (52 KB)

==================================================

downloaded 52 KB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'graphics' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/nlme_3.1-139.tar.gz'

Content type 'application/x-gzip' length 793473 bytes (774 KB)

==================================================

downloaded 774 KB

trying URL 'https://cran.rstudio.com/src/contrib/Matrix_1.2-17.tar.gz'

Content type 'application/x-gzip' length 1860456 bytes (1.8 MB)

==================================================

downloaded 1.8 MB

Warning in download.packages(packages, destdir = file.path(mainDir, subDir)) :

no package 'splines' at the repositories

trying URL 'https://cran.rstudio.com/src/contrib/stringr_1.4.0.tar.gz'

Content type 'application/x-gzip' length 135777 bytes (132 KB)

==================================================

downloaded 132 KB

trying URL 'https://cran.rstudio.com/src/contrib/labeling_0.3.tar.gz'

Content type 'application/x-gzip' length 10722 bytes (10 KB)

==================================================

downloaded 10 KB

trying URL 'https://cran.rstudio.com/src/contrib/munsell_0.5.0.tar.gz'

Content type 'application/x-gzip' length 182653 bytes (178 KB)

==================================================

downloaded 178 KB

trying URL 'https://cran.rstudio.com/src/contrib/RColorBrewer_1.1-2.tar.gz'

Content type 'application/x-gzip' length 11532 bytes (11 KB)

==================================================

downloaded 11 KB

trying URL 'https://cran.rstudio.com/src/contrib/lattice_0.20-38.tar.gz'

Content type 'application/x-gzip' length 359031 bytes (350 KB)

==================================================

downloaded 350 KB

trying URL 'https://cran.rstudio.com/src/contrib/colorspace_1.4-1.tar.gz'

Content type 'application/x-gzip' length 2152594 bytes (2.1 MB)

==================================================

downloaded 2.1 MB

trying URL 'https://cran.rstudio.com/src/contrib/stringi_1.4.3.tar.gz'

Content type 'application/x-gzip' length 7290890 bytes (7.0 MB)

==================================================

downloaded 7.0 MB

[,1] [,2]

[1,] "dplyr" "/Users/ihongdon/Downloads/r-pkg/dplyr_0.8.0.1.tar.gz"

[2,] "ggplot2" "/Users/ihongdon/Downloads/r-pkg/ggplot2_3.1.1.tar.gz"

[3,] "assertthat" "/Users/ihongdon/Downloads/r-pkg/assertthat_0.2.1.tar.gz"

[4,] "glue" "/Users/ihongdon/Downloads/r-pkg/glue_1.3.1.tar.gz"

[5,] "magrittr" "/Users/ihongdon/Downloads/r-pkg/magrittr_1.5.tar.gz"

[6,] "pkgconfig" "/Users/ihongdon/Downloads/r-pkg/pkgconfig_2.0.2.tar.gz"

[7,] "R6" "/Users/ihongdon/Downloads/r-pkg/R6_2.4.0.tar.gz"

[8,] "Rcpp" "/Users/ihongdon/Downloads/r-pkg/Rcpp_1.0.1.tar.gz"

[9,] "rlang" "/Users/ihongdon/Downloads/r-pkg/rlang_0.3.4.tar.gz"

[10,] "tibble" "/Users/ihongdon/Downloads/r-pkg/tibble_2.1.1.tar.gz"

[11,] "tidyselect" "/Users/ihongdon/Downloads/r-pkg/tidyselect_0.2.5.tar.gz"

[12,] "cli" "/Users/ihongdon/Downloads/r-pkg/cli_1.1.0.tar.gz"

[13,] "crayon" "/Users/ihongdon/Downloads/r-pkg/crayon_1.3.4.tar.gz"

[14,] "fansi" "/Users/ihongdon/Downloads/r-pkg/fansi_0.4.0.tar.gz"

[15,] "pillar" "/Users/ihongdon/Downloads/r-pkg/pillar_1.3.1.tar.gz"

[16,] "purrr" "/Users/ihongdon/Downloads/r-pkg/purrr_0.3.2.tar.gz"

[17,] "utf8" "/Users/ihongdon/Downloads/r-pkg/utf8_1.1.4.tar.gz"

[18,] "digest" "/Users/ihongdon/Downloads/r-pkg/digest_0.6.18.tar.gz"

[19,] "gtable" "/Users/ihongdon/Downloads/r-pkg/gtable_0.3.0.tar.gz"

[20,] "lazyeval" "/Users/ihongdon/Downloads/r-pkg/lazyeval_0.2.2.tar.gz"

[21,] "MASS" "/Users/ihongdon/Downloads/r-pkg/MASS_7.3-51.4.tar.gz"

[22,] "mgcv" "/Users/ihongdon/Downloads/r-pkg/mgcv_1.8-28.tar.gz"

[23,] "plyr" "/Users/ihongdon/Downloads/r-pkg/plyr_1.8.4.tar.gz"

[24,] "reshape2" "/Users/ihongdon/Downloads/r-pkg/reshape2_1.4.3.tar.gz"

[25,] "scales" "/Users/ihongdon/Downloads/r-pkg/scales_1.0.0.tar.gz"

[26,] "viridisLite" "/Users/ihongdon/Downloads/r-pkg/viridisLite_0.3.0.tar.gz"

[27,] "withr" "/Users/ihongdon/Downloads/r-pkg/withr_2.1.2.tar.gz"

[28,] "nlme" "/Users/ihongdon/Downloads/r-pkg/nlme_3.1-139.tar.gz"

[29,] "Matrix" "/Users/ihongdon/Downloads/r-pkg/Matrix_1.2-17.tar.gz"

[30,] "stringr" "/Users/ihongdon/Downloads/r-pkg/stringr_1.4.0.tar.gz"

[31,] "labeling" "/Users/ihongdon/Downloads/r-pkg/labeling_0.3.tar.gz"

[32,] "munsell" "/Users/ihongdon/Downloads/r-pkg/munsell_0.5.0.tar.gz"

[33,] "RColorBrewer" "/Users/ihongdon/Downloads/r-pkg/RColorBrewer_1.1-2.tar.gz"

[34,] "lattice" "/Users/ihongdon/Downloads/r-pkg/lattice_0.20-38.tar.gz"

[35,] "colorspace" "/Users/ihongdon/Downloads/r-pkg/colorspace_1.4-1.tar.gz"

[36,] "stringi" "/Users/ihongdon/Downloads/r-pkg/stringi_1.4.3.tar.gz"

위에 다운로드된 패키지들의 리스트를 보면 알 수 있는 것처럼, 'dplyr'과 'ggplot2'의 두 개 패키지를 다운로드 하려고 했더니 이들이 의존성을 가지고 있는 [3] 'assertthat' 패키지부터 ~ [36] 'stringi' 패키지까지 34개의 패키지가 추가로 다운로드 되었습니다.

외부의 인터넷 연결이 되는 환경에서 다운받아 놓은 이들 R packages 파일들을 저장매체에 저장하여 가져가서 폐쇄망으로 되어 있는 서버에 복사를 한 후에, 수작업으로 R package 설치하면 되겠습니다. (이때 의존성 있는 패키지들까지 알아서 다 설치가 되도록 여러번 설치 작업을 반복해주면 됩니다.

아래 코드를 사용하시면 다운로드 받아놓은 모든 패키지의 리스트를 읽어와서 수동으로 R 패키지 설치를 할 수 있습니다.

## set working directory
setwd("C:/Users/hdlee/Documents/R") # set with yours

## getting the list of R packages downloaded
src_pkgs <- list.files("C:/Users/hdlee/Documents/R") # use yours

## install R packages manually using binary files
install.packages(src_pkgs, repos = NULL, type = "source")

##==============================================##

폐쇄망 환경에서 Greenplum DB에 R 패키지 설치하는 방법은

== > http://gpdbkr.blogspot.com/2019/12/greenplum-6-plr-r.html

==> https://rfriend.tistory.com/442

포스팅을 참고하세요.

##==============================================##

많은 도움이 되었기를 바랍니다.

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] R 패키지 함수의 소스 코드를 볼 수 있는 방법 (how to see function's source codes in R package) (0)	2019.10.22
[R] 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고 내림차순 정렬하기 (16)	2019.10.15
[R] 그룹 별 행 합이 최대인 행만 선별하기 (Selecting rows which the RowSum is maximum per groups) (2)	2019.02.22
[R] 여러개의 데이터프레임을 리스트로 묶기 (how to combine many DataFrames into a List) : mget() (4)	2018.03.24
[R] 문자열을 특정 길이로 만들고, 빈 자리는 '0'으로 채우기, 소수점 길이 지정하기 : sprintf {base} (6)	2017.09.17

Posted by Rfriend

,

[R] 그룹 별 행 합이 최대인 행만 선별하기 (Selecting rows which the RowSum is maximum per groups)

R 분석과 프로그래밍/R 데이터 전처리 2019. 2. 22. 20:47

이번 포스팅에서는 행 기준으로 숫자형 변수들의 합을 구한 다음에, 그룹별로 행 기준 합이 최대인 전체 행을 선별하는 방법을 소개하겠습니다.

말로 설명한 내용만으로는 얼른 이해가 안 올 수도 있겠는데요, 이번에 해볼 내용은 아래의 이미지를 참고하시면 이해가 쉬울 듯 합니다.

예제로 사용할 하나의 그룹 변수(V1)와 나머지 9개의 숫자형 변수(V2~V10)로 구성된 간단한 DataFrame을 만들어보겠습니다.

> ##------------------------------------------------------

> ## selecting distinct object using dplyr chain operator

> ##------------------------------------------------------

>

> rm(list=ls())

>

> set.seed(123) # for reproducibility

> V1 <- c(rep("apple", 5), rep("banana", 5), rep("tomato", 5)) # group

> V2 <- sample(x=1:10, size=15, replace=T)

> V3 <- sample(x=1:10, size=15, replace=T)

> V4 <- sample(x=1:10, size=15, replace=T)

> V5 <- sample(x=1:10, size=15, replace=T)

> V6 <- sample(x=1:10, size=15, replace=T)

> V7 <- sample(x=1:10, size=15, replace=T)

> V8 <- sample(x=1:10, size=15, replace=T)

> V9 <- sample(x=1:10, size=15, replace=T)

> V10 <- sample(x=1:10, size=15, replace=T)

>

> df <- data.frame(V1, V2, V3, V4, V5, V6, V7, V8, V9, V10)

> df

V1 V2 V3 V4 V5 V6 V7 V8 V9 V10

1 apple 3 9 10 2 7 3 2 9 7

2 apple 8 3 10 3 1 4 7 10 4

3 apple 5 1 7 5 4 7 4 7 4

4 apple 9 4 8 3 3 4 7 5 3

5 apple 10 10 1 9 9 2 4 2 4

6 banana 1 9 5 1 5 3 2 10 10

7 banana 6 7 8 5 9 7 8 4 2

8 banana 9 7 3 8 9 5 1 1 1

9 banana 6 10 4 2 8 8 5 10 2

10 banana 5 7 3 6 5 2 6 8 7

11 tomato 10 8 2 3 8 5 6 2 7

12 tomato 5 6 5 2 7 10 4 6 9

13 tomato 7 6 5 8 8 9 5 10 7

14 tomato 6 3 4 9 1 9 10 6 8

15 tomato 2 2 2 4 5 2 5 5 6

>

> rm(V1, V2, V3, V4, V5, V6, V7, V8, V9, V10)

>

rowSums() 함수를 사용하여서 행(row) 기준의 숫자형 변수들 모두에 대해 합계를 구하여 'V_sum' 이라는 새로운 변수를 추가해보겠습니다.

> # summation in a row direction

> df$V_sum <- rowSums(df[,2:10])

> df

V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V_sum

1 apple 3 9 10 2 7 3 2 9 7 52

2 apple 8 3 10 3 1 4 7 10 4 50

3 apple 5 1 7 5 4 7 4 7 4 44

4 apple 9 4 8 3 3 4 7 5 3 46

5 apple 10 10 1 9 9 2 4 2 4 51

6 banana 1 9 5 1 5 3 2 10 10 46

7 banana 6 7 8 5 9 7 8 4 2 56

8 banana 9 7 3 8 9 5 1 1 1 44

9 banana 6 10 4 2 8 8 5 10 2 55

10 banana 5 7 3 6 5 2 6 8 7 49

11 tomato 10 8 2 3 8 5 6 2 7 51

12 tomato 5 6 5 2 7 10 4 6 9 54

13 tomato 7 6 5 8 8 9 5 10 7 65

14 tomato 6 3 4 9 1 9 10 6 8 56

15 tomato 2 2 2 4 5 2 5 5 6 33

위의 행 기준 합계로 보면 'apple' 그룹에서는 1번째 행의 합이 52로 가장 크며, 'banana' 그룹에서는 7번째 행의 합이 56으로서 가장 크고, 'tomato' 그룹에서는 13번째 행의 합이 65로서 가장 큽니다. 이를 1번째, 7번째, 13번째 전체 행을 선별해보겠습니다. (빨간색으로 표시한 부분)

> library(dplyr)

> df_group_distinct_max <- df %>%

+ arrange(V1, desc(V_sum)) %>%

+ group_by(V1) %>% slice(1:1)

>

> df_group_distinct_max <- data.frame(df_group_distinct_max[1:10])

> df_group_distinct_max

V1 V2 V3 V4 V5 V6 V7 V8 V9 V10

1 apple 3 9 10 2 7 3 2 9 7

2 banana 6 7 8 5 9 7 8 4 2

3 tomato 7 6 5 8 8 9 5 10 7

* dplyr 패키지 사용법은

https://rfriend.tistory.com/234 ,

https://rfriend.tistory.com/236

를 참고하시기 바랍니다.

많은 도움이 되었기를 바랍니다.

이번 포스팅이 도움이 되었다면 아래의 '공감~'를 꾹 눌러주세요. ^^

728x90

저작자표시 비영리 변경금지

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고 내림차순 정렬하기 (16)	2019.10.15
[R] 원하는 R 패키지와 의존성 있는 R 패키지를 모두 한꺼번에 다운로드 하기 (tools::package_dependencies(), download.packages()) (4)	2019.04.27
[R] 여러개의 데이터프레임을 리스트로 묶기 (how to combine many DataFrames into a List) : mget() (4)	2018.03.24
[R] 문자열을 특정 길이로 만들고, 빈 자리는 '0'으로 채우기, 소수점 길이 지정하기 : sprintf {base} (6)	2017.09.17
[R] 대용량 text 데이터 빠르게 불러오기 : data.table 패키지의 fread() 함수 (0)	2017.09.02

Posted by Rfriend

,

R, Python 분석과 프로그래밍의 친구 (by R Friend)

'R 분석과 프로그래밍'에 해당되는 글 289건

[R] R 패키지 함수의 소스 코드를 볼 수 있는 방법 (how to see function's source codes in R package)

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] 시계열 정수의 순차 3개 묶음 패턴 별 개수를 구하고 내림차순 정렬하기

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] ggplot2 의 커널 밀도 곡선(Kernel Density Curve)의 최대 피크값 좌표구하고 수직선 추가하기

'R 분석과 프로그래밍 > R 그래프_시각화' 카테고리의 다른 글

[R] DataFrame에서 특정 조건에 해당하는 행과 앞, 뒤 2개 행을 같이 제거하는 방법

'R 분석과 프로그래밍 > R 프로그래밍' 카테고리의 다른 글

수식 표기를 영어로 읽는 방법 (how to read mathematical notation in English)

'R 분석과 프로그래밍 > R 기계학습' 카테고리의 다른 글

[R] R Shiny 로 두 집단 간 평균 차이 t-검정(t-Test) 신뢰수준별 신뢰구간 구하는 웹 애플리케이션 만들기

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] R Shiny로 두 연속형 변수 간 상관계수, 산점도와 회귀선 그리는 앱 애플리케이션 만들기

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] R Shiny로 연속형 변수 별 요약 통계량 조회하는 Interactive App 만들기

'R 분석과 프로그래밍 > R 동적 문서(Dynamic Document)' 카테고리의 다른 글

[R] 원하는 R 패키지와 의존성 있는 R 패키지를 모두 한꺼번에 다운로드 하기 (tools::package_dependencies(), download.packages())

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

[R] 그룹 별 행 합이 최대인 행만 선별하기 (Selecting rows which the RowSum is maximum per groups)

'R 분석과 프로그래밍 > R 데이터 전처리' 카테고리의 다른 글

카테고리

태그목록

티스토리툴바