[R 지리공간 데이터 분석] R에서의 좌표계, 좌표 참조 시스템 (CRS, Coordinate Reference Systems in R)
R 분석과 프로그래밍/R 지리공간데이터 분석 2021. 2. 13. 21:13지난번 포스팅에서는 3가지 종류의 레스터 클래스 객체로서 RasterLayer 클래스, RasterBrick 클래스, RasterStack 클래스가 있고, 각 특성은 무엇인지, 그리고 R raster 패키지를 사용해서 각 레스터 클래스 객체를 어떻게 만들 수 있는지 살펴보았습니다. (rfriend.tistory.com/617)
또 이전 포스팅 rfriend.tistory.com/596 에서 좌표계가 무엇이고, 벡터 데이터를 다룰 때 사용하는 sf 패키지를 사용해서 좌표계를 지정하고 확인하는 방법을 소개한 적이 있습니다.
이번 포스팅에서는 지리 공간 데이터 분석에서 가장 기본이 되고 또 처음에 확인을 해보아야 하는 좌표계, 좌표 참조 시스템(CRS, Coordinate Reference Systems)에 대해서 좀더 자세하게 소개하겠습니다. (이하, CRS는 "좌표계"로 부르겠습니다.)
(1) 좌표계, 좌표 참조 시스템 (CRS, Coordinate Reference Systems)은 무엇인가?
(2) 지리 좌표계 (Geographic Coordinate Reference Systems)
(3) 투영(투사) 좌표계 (Projected Coordinate Reference Systems)
(4) R에서의 좌표계 (Coordinate Reference Systems in R)

(1) 좌표계 (CRS, Coordinate Reference Systems)는 무엇인가?
좌표계 (Coordinate Reference Systems) 는 지리공간 데이터를 저장/처리/분석하는데 있어서 지구의 표면을 어떻게 데이터의 공간 원소들로 표현할 지를 정의합니다. 좌표계는 좌표를 기반으로 국소, 지역, 또는 전지구적으로 지리상의 객체를 위치시킬 때 사용하는 참조 시스템입니다. 좌표계는 특정 지도 투영법(map projection)을 정의하고, 서로 다른 좌표계 간의 변환 (CRS transformtations)을 할 수 있도록 해줍니다.
좌표계는 지리 좌표계 (Geographic CRSs) 이거나 또는 투영 좌표계 (Projected CRSs) 인데요, 아래에 각각에 대해서 하나씩 설명하겠습니다.
(2) 지리 좌표계 (Geographic Coordinate Reference Systems)
지리 좌표계는 지구의 표면을 위도(Latitude)와 경도(Longitude) 의 두 개의 값을 사용해서 위치를 정의합니다. 위도(Latitude)는 적도면(Equator plane)으로 부터 남과 북 방향으로의 거리를 각도로 나타낸 것입니다. 경도(Longitude)는 본초 자오선 면(the Prime Meridian plane)으로 부터 동-서 방향으로의 거리를 각도로 나타낸 것입니다. 즉, 지리 좌표계에서의 거리는 미터(meters)가 아니라 각도(anglular distance)를 사용해서 측정합니다.
[ 위도와 경도 (Latitude and Longitude) ]
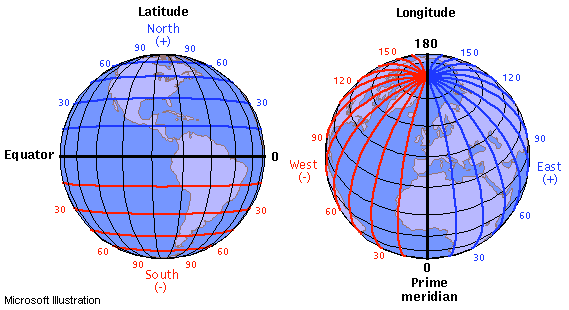
지리 좌표계에서의 지구 표면은 구면의 표면(Spherical surface) 또는 타원의 표면(Ellipsoidal surface)으로 표현됩니다.
구면 모델 (Spherical models) 은 지구가 주어진 반경(radius)으로 부터 완벽한 구면이라고 가정합니다. 구면 모델은 단순하고 계산이 빠르다는 장점이 있지만, 부정확하기 때문에 많이 이용되지는 않습니다. (실제의 지구 표면은 아래의 그림처럼 울퉁불퉁하며, 완벽한 구면이 아니기 때문입니다.)
타원 모델(Ellipsoidal models)은 적도 반지름(the equatorial radius)과 극 반지름(the polar radius)의 두 개의 모수를 사용해서 지구 표면을 정의합니다. 실제 지구는 아래의 그림처럼 위아래가 눌려서 옆으로 찌그러져 있으므로 타원 모델로 지구 표면을 표현하는 것이 구면 모델보다 더 적합합니다. (적도 반지름이 극 반지름보다 약 11.5 km 더 길이가 깁니다.)
[ 지구의 표면, 지오이드(GEOID), 타원(Ellipse), and 구(Sphere) ]
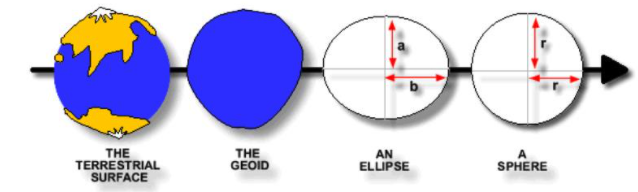
타원면(Ellipsoids)은 좌표계(CRSs)의 광의의 구성요소 중의 하나인 'the datum' 의 한 부분입니다. 'the datum'은 PROJ CRS 라이브러리 안의 'ellps' 모수로 무슨 타원면을 사용할지에 대한 정보와, 데카르트 좌표(Cartesian coordinates)와 지구 표면 위치 간의 정확한 관계에 대한 정보를 포함하고 있습니다. 이러한 추가적인 세부사항들은 'proj4string' 표기의 'towgs84' 매개변수에 저장이 되어 있습니다.
이러한 타원면의 the datum 정보들은 지구 표면의 지역적인 변이를 허용합니다. (가령, 큰 산맥이 있다면 지역 좌표계에 반영할 수 있음.)
the datum 에는 지역적 데이터(local datum)와 지심에서 바라 본 데이터(geocentric datum)의 두 종류가 있습니다. 'NAD83'과 같은 지역적 데이터(local datum)에서는 타원 표면이 특정 위치의 표면과 정렬이 되어 이동이 되어 있습니다. 반면에, 'WGS84'와 같은 지심에서 바라 본 데이터 (geocentric datum) 에서는 지구 중력의 중심이 중심 위치가 되며, 투사의 정확도가 특정 위치에 최적화되어 있지는 않습니다.
(3) 투영(투사) 좌표계 (Projected Coordinate Reference Systems)
투영 좌표계(Projected Coordinate Reference Systems)는 암묵적으로 평평한 표면 위의 데카르트 좌표를 기반으로 합니다. 투영 좌표계는 원점(origin), x축과 y축, 그리고 미터(meters)와 같은 선형 측정 단위를 가지고 있습니다. 모든 투영 좌표계는 지리 좌표계(geographic CRSs)를 기반으로 하며, 3차원의 지구 표면을 투영 좌표계의 x축(동-서)와 y축(남-북)의 값으로 변환하는 지도 투사에 의존합니다.
평평한 평면을 가정하고 투영 변환을 하기 때문에 면적, 방향, 거리, 모양 등에 대한 왜곡이 발생하게 됩니다. 투영된 좌표계는 이들 중 단지 하나 혹은 두개의 특성 만을 보존할 수 있습니다. 투영 후 좌표계가 보존하는 특성이 무엇이냐에 따라서 보통 이름이 지어지는데요, 가령, 등면적 보존 면적 (equal-area preserve area), 방위각 보존 방향 (azimuthal preserve direction), 등거리 보존 거리 (equidistant preserve distance), 등각 보존 국소 형태 (conformal preserve local shape) 등과 같이 부릅니다.
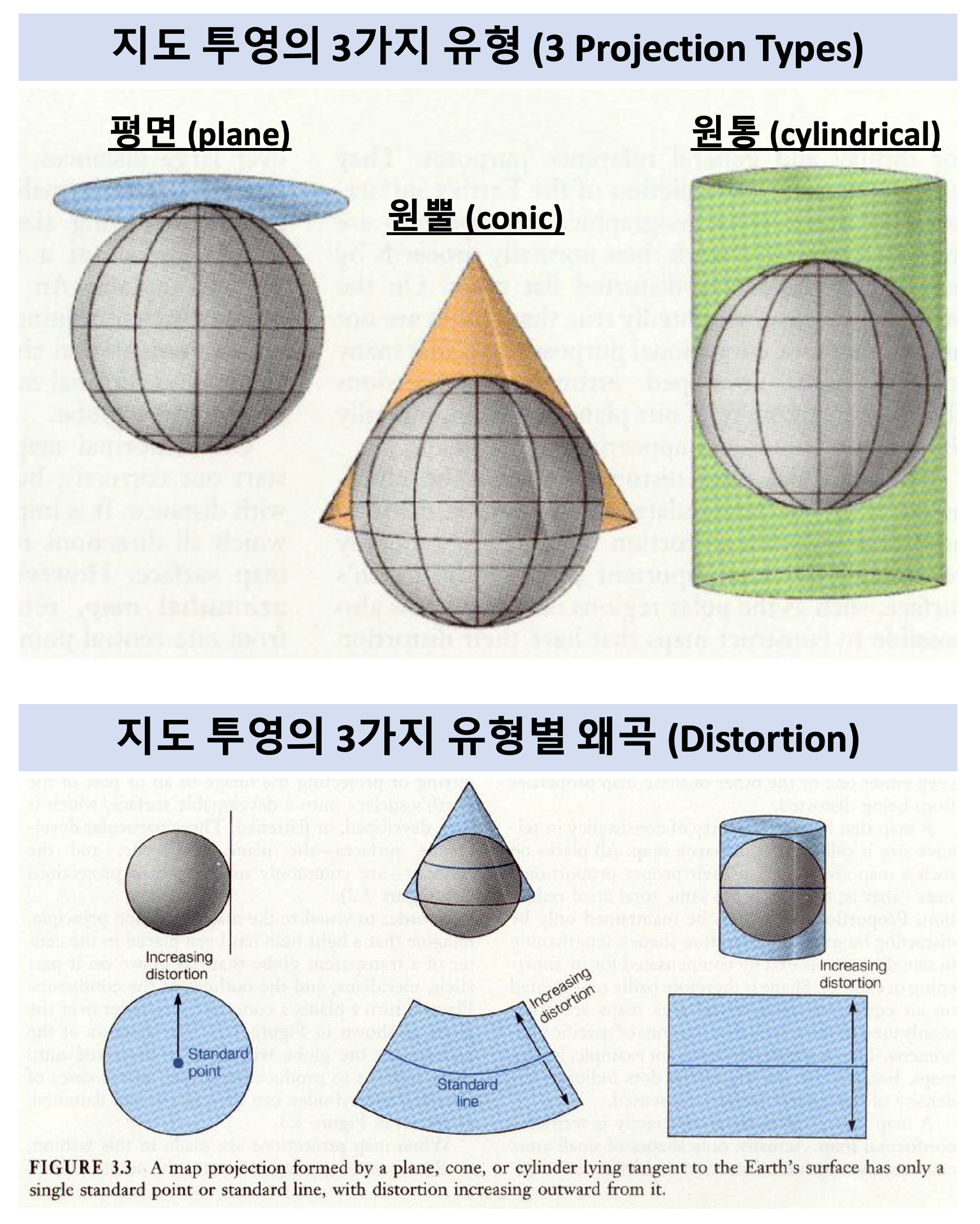
투영의 유형과 원리(projection types and principles)에는 크게 평면(planar), 원뿔(conic), 실린더(cylindrical) 의 3가지 그룹이 있습니다. (아래 그림 참조)
(a) 평면 투영 (planar projection) 은 데이터를 지구와 접촉하는 하나의 점이나 접촉하는 선과 함께 평평한 표면에 투사를 합니다. 평면 투영법은 일반적으로 극 지방(polar regions)을 매핑할 때 사용됩니다. 투영의 기준(시작)이 되는 표준 점(standard point)으로 부터 멀어질 수록 데이터 왜곡이 심해집니다.
(b) 원뿔 투영 (conic projection)에서는 지구의 표면이 원뿔과 접촉하는 하나의 선이나 두개의 선들로 원뿔에 투영이 됩니다. 원뿔과 만나는 선인 표준 선(standard line)에서 왜곡이 가장 작고, 표준 선으로부터 멀어질 수록 왜곡이 심해집니다. 따라서 중간 위도 지역(mid-latitude areas)의 투영법으로 가장 적합합니다.
(c) 원통 투영 (cylindrical projection) 은 지구의 표면을 원통과 접촉하는 하나의 선이나 두개의 선들을 원통에 투사합니다. 원통 투영은 보통 지구 전체(entire world)를 매핑할 때 많이 사용합니다.
[ 지도 투영의 3가지 유형(Projection types)과 각 투영 유형별 왜곡(Distortion) ]
(4) R에서의 좌표계 (CRSs in R)
R에서 좌표계를 표현할 때는 (a) epsg 코드 (epsg code)나 또는 (b) proj4string 정의 (proj4string definition)를 사용합니다. 이들 두 가지의 좌표계 표현 방법별로 장단점이 있습니다.
(a) epsg 코드는 더 짧고, 따라서 기억하기 쉽습니다. 그리고 epsg 코드는 단 하나의 잘 정의된 좌표계를 지칭합니다. (EPSG: European Petroleum Survey Group, 지도 투영과 datums 에 대한 좌표계 정보 데이터베이스를 제공함)
반면에, (b) proj4string 정의는 투사 유형이나 datum, 타원체 등의 다른 모수들을 구체화할 수 있는 유연성이 있다는 장점이 있는 대신에, 사용자가 구체화를 해야 하므로 길고 복잡하며 기억하기 어렵습니다.
지리공간 R 패키지들은 PROJ 라이브러리를 사용하여 광범위한 좌표계(CRSs)를 지원합니다. R의 rgdal::make_EPSG() 함수를 사용하면 R이 지원하는 투영 좌표계의 리스트를 data.frame 형태로 반환받아 확인할 수 있습니다. 아래에 조회해본 결과, 현재 6,609개의 좌표계를 지원하고 있으며, EPSG 코드 (code), 설명 (note), proj4string 정의 (prj4), 투영 방법 (prj_method) 의 4개 칼럼으로 좌표계 정보를 제공합니다. 가령 'EPSG코드가 4326' 인 행을 조회해보면 note에 'WGS 84' (World Geodetic System 1984) 라고 설명이 나오는군요.
## ========================================
## Coordinate Reference Systems (CRS) in R
## ========================================
crs_rgdal = rgdal::make_EPSG()
str(crs_rgdal)
# 'data.frame': 6609 obs. of 4 variables:
# $ code : int 3819 3821 3822 3823 3824 3887 3888 3889 3906 4000 ...
# $ note : chr "HD1909" "TWD67" "TWD97" "TWD97" ...
# $ prj4 : chr "+proj=longlat +ellps=bessel +no_defs +type=crs" "+proj=longlat +ellps=aust_SA +no_defs +type=crs" "+proj=geocent +ellps=GRS80 +units=m +no_defs +type=crs" "+proj=longlat +ellps=GRS80 +no_defs +type=crs" ...
# $ prj_method: chr "(null)" "(null)" "(null)" "(null)" ...
head(crs_rgdal, 10)
# code note prj4 prj_method
# 1 3819 HD1909 +proj=longlat +ellps=bessel +no_defs +type=crs (null)
# 2 3821 TWD67 +proj=longlat +ellps=aust_SA +no_defs +type=crs (null)
# 3 3822 TWD97 +proj=geocent +ellps=GRS80 +units=m +no_defs +type=crs (null)
# 4 3823 TWD97 +proj=longlat +ellps=GRS80 +no_defs +type=crs (null)
# 5 3824 TWD97 +proj=longlat +ellps=GRS80 +no_defs +type=crs (null)
# 6 3887 IGRS +proj=geocent +ellps=GRS80 +units=m +no_defs +type=crs (null)
# 7 3888 IGRS +proj=longlat +ellps=GRS80 +no_defs +type=crs (null)
# 8 3889 IGRS +proj=longlat +ellps=GRS80 +no_defs +type=crs (null)
# 9 3906 MGI 1901 +proj=longlat +ellps=bessel +no_defs +type=crs (null)
# 10 4000 MOLDREF99 +proj=geocent +ellps=GRS80 +units=m +no_defs +type=crs (null)
## EPSG 4326 : WGS 84
crs_rgdal[crs_rgdal$code == 4326,]
# code note prj4 prj_method
# 261 4326 WGS 84 +proj=longlat +datum=WGS84 +no_defs +type=crs (null)
- (4-1) 벡터 데이터의 좌표계 확인: sf 패키지의 st_crs() 함수
- (4-2) 레스터 지리 데이터의 좌표계 확인: raster 패키지의 projection() 함수
(4-1) 벡터 데이터의 좌표계 (CRSs in Vector geographic data)
벡터 지리 데이터에 대해서는 sf 패키지의 st_crs() 함수를 사용해서 좌표계를 확인할 수 있습니다.
아래의 예에서는 spDataLarge 패키지에 들어있는 Zion 국립 공원의 경계를 다각형면(Polygon)으로 나타내는 zion.gpkg 벡터 데이터를 st_read() 함수로 불러와서, st_crs() 함수로 좌표계를 조회해 본 것입니다. 좌표계가 'User input: UTM Zone 12, Northern Hemisphere' 라고 나오는군요.
## st_read() : read vector dataset in R sf package
library(sf)
vector_filepath = system.file("vector/zion.gpkg", package = "spDataLarge")
vector_zion = st_read(vector_filepath)
# Reading layer `zion' from data source `/Library/Frameworks/R.framework/Versions/4.0/Resources/library/spDataLarge/vector/zion.gpkg' using driver `GPKG'
# Simple feature collection with 1 feature and 11 fields
# geometry type: POLYGON
# dimension: XY
# bbox: xmin: 302903.1 ymin: 4112244 xmax: 334735.5 ymax: 4153087
# projected CRS: UTM Zone 12, Northern Hemisphere
## -- st_crs() : get CRS in vector dataset
st_crs(vector_zion)
# Coordinate Reference System:
# User input: UTM Zone 12, Northern Hemisphere
# wkt:
# BOUNDCRS[
# SOURCECRS[
# PROJCRS["UTM Zone 12, Northern Hemisphere",
# BASEGEOGCRS["GRS 1980(IUGG, 1980)",
# DATUM["unknown",
# ELLIPSOID["GRS80",6378137,298.257222101,
# LENGTHUNIT["metre",1,
# ID["EPSG",9001]]]],
# PRIMEM["Greenwich",0,
# ANGLEUNIT["degree",0.0174532925199433]]],
# CONVERSION["UTM zone 12N",
# METHOD["Transverse Mercator",
# ID["EPSG",9807]],
# PARAMETER["Latitude of natural origin",0,
# ANGLEUNIT["degree",0.0174532925199433],
# ID["EPSG",8801]],
# PARAMETER["Longitude of natural origin",-111,
# ANGLEUNIT["degree",0.0174532925199433],
# ID["EPSG",8802]],
# PARAMETER["Scale factor at natural origin",0.9996,
# SCALEUNIT["unity",1],
# ID["EPSG",8805]],
# PARAMETER["False easting",500000,
# LENGTHUNIT["Meter",1],
# ID["EPSG",8806]],
# PARAMETER["False northing",0,
# LENGTHUNIT["Meter",1],
# ID["EPSG",8807]],
# ID["EPSG",16012]],
# CS[Cartesian,2],
# AXIS["(E)",east,
# ORDER[1],
# LENGTHUNIT["Meter",1]],
# AXIS["(N)",north,
# ORDER[2],
# LENGTHUNIT["Meter",1]]]],
# TARGETCRS[
# GEOGCRS["WGS 84",
# DATUM["World Geodetic System 1984",
# ELLIPSOID["WGS 84",6378137,298.257223563,
# LENGTHUNIT["metre",1]]],
# PRIMEM["Greenwich",0,
# ANGLEUNIT["degree",0.0174532925199433]],
# CS[ellipsoidal,2],
# AXIS["latitude",north,
# ORDER[1],
# ANGLEUNIT["degree",0.0174532925199433]],
# AXIS["longitude",east,
# ORDER[2],
# ANGLEUNIT["degree",0.0174532925199433]],
# ID["EPSG",4326]]],
# ABRIDGEDTRANSFORMATION["Transformation from GRS 1980(IUGG, 1980) to WGS84",
# METHOD["Position Vector transformation (geog2D domain)",
# ID["EPSG",9606]],
# PARAMETER["X-axis translation",0,
# ID["EPSG",8605]],
# PARAMETER["Y-axis translation",0,
# ID["EPSG",8606]],
# PARAMETER["Z-axis translation",0,
# ID["EPSG",8607]],
# PARAMETER["X-axis rotation",0,
# ID["EPSG",8608]],
# PARAMETER["Y-axis rotation",0,
# ID["EPSG",8609]],
# PARAMETER["Z-axis rotation",0,
# ID["EPSG",8610]],
# PARAMETER["Scale difference",1,
# ID["EPSG",8611]]]]
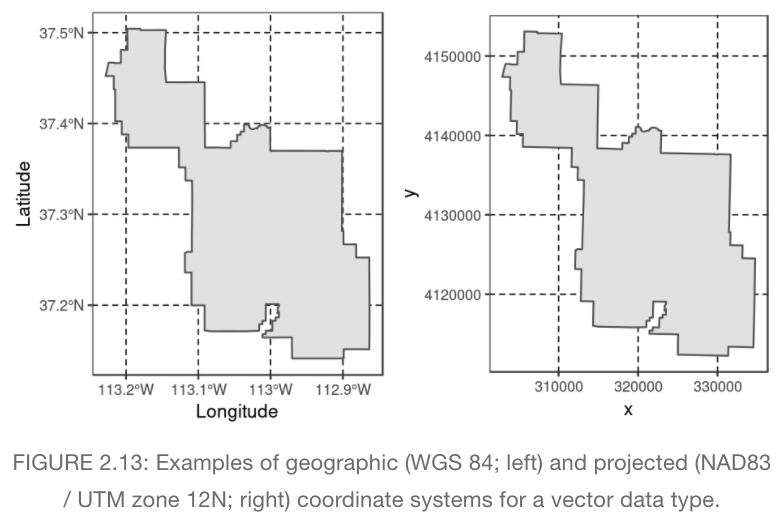
만약 좌표계가 비어있거나 잘못 입력되어 있는 경우 st_set_crs(vector_object, EPSG code) 구문으로 좌표계를 설정할 수 있습니다. 단, 아래의 경고 문구처럼 "st_set_crs() 함수는 좌표계를 변경하는 것이 투영 데이터를 변환하는 것은 아니며, 투영 데이터 변환을 하려면 st_transform() 함수를 이용 (st_crs<- : replacing crs does not reproject data; use st_transform for that)"해야 합니다.
## -- st_set_crs() : setting a CRS (coordinate reference system)
vector_zion_2 = st_set_crs(vector_zion, 4326) # set CRS with EPSG 4326 code
# Warning message:
# st_crs<- : replacing crs does not reproject data; use st_transform for that
[ 벡터 데이터: 지리 좌표계 (WGS 84; 왼쪽) vs. 투영 좌표계 (NAD83/ UTM zone 12N; 오른쪽) ]
(4-2) 레스터 데이터에서 좌표계 (CRSs in Raster data)
레스터 모델의 객체에 대해서는 raster 패키지의 projection() 함수를 사용해서 좌표계를 확인하거나 설정할 수 있습니다.
아래 예는 R spDataLarge 패키지에 포함되어 있는 strm.tif 파일을 raster() 함수를 사용해 레스터 데이터로 읽어와서, projection() 함수로 좌표계를 확인해본 것입니다.
## -- raster::projection() : get or set CRS in raster* objects
library(raster)
raster_filepath = system.file("raster/srtm.tif", package = "spDataLarge")
new_raster = raster(raster_filepath)
projection(new_raster) # get CRS in raster objects
# [1] "+proj=longlat +datum=WGS84 +no_defs"
레스터 데이터에 대해서 좌표계를 새로 설정할 때도 역시 projection() 함수를 사용합니다. 벡터 데이터의 경우 좌표계를 설정할 때 'EPSG 코드'나 'Proj4string 정의' 모두 사용 가능한 반면에, 레스터 데이터는 'Proj4string 정의'만 사용할 수 있습니다.
## -- set CRS for raster objects
projection(new_raster) = "+proj=utm +zone=12 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0
+units=m +no_defs"
# Warning message:
# In showSRID(uprojargs, format = "PROJ", multiline = "NO", prefer_proj = prefer_proj) :
# Discarded datum Unknown based on GRS80 ellipsoid in Proj4 definition
projection(new_raster)
# [1] "+proj=utm +zone=12 +ellps=GRS80 +units=m +no_defs"
[ Reference ]
Geographic data in R - 'CRSs' : geocompr.robinlovelace.net/spatial-class.html
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)

'R 분석과 프로그래밍 > R 지리공간데이터 분석' 카테고리의 다른 글
| [R 지리공간 데이터 분석] 벡터 데이터의 속성 정보 가져오기 (subset attributes from vector data) (0) | 2021.02.21 |
|---|---|
| [R 지리공간 데이터 분석] 공간의 단위 (Spatial Units) (2) | 2021.02.14 |
| [R 지리공간 데이터 분석] 3가지 레스터 클래스 (Raster Classes) (0) | 2021.02.12 |
| [R 지리공간 데이터 분석] 레스터 데이터 (Raster Data) (0) | 2021.01.24 |
| [R 지리공간 데이터 분석] sf 패키지와 sp 패키지 간 클래스 변환 (conversion b/w R sf and sp classes) (0) | 2021.01.04 |



