지난번 포스팅에서는 독립된 2개 표본의 평균 차이를 검정하는 t-test 에 대해서 알아보았습니다.
이번 포스팅에서는 Python을 이용한 짝을 이룬 표본의 평균 차이를 검정하는 paired t-test 에 대해서 소개하겠습니다.
(R을 이용한 짝을 이룬 표본에 대한 평균 차이 검정은 https://rfriend.tistory.com/128 를 참고하세요)
짝을 이룬 t-test(paired t-test)는 짝을 이룬 측정치(paired measurements)의 평균 차이가 있는지 없는지를 검정하는 방법입니다. 데이터 값이 짝을 이루어서 측정되었다는 것에 대해 예를 들어보면, 사람들의 그룹에 대해 신약 효과를 알아보기 위해 (즉, 신약 투약 전과 후의 평균의 차이가 있는지) 신약 투약 전과 후(before-and-after)를 측정한 데이터를 생각해 볼 수 있습니다.
[ One sample t-test vs. Independent samples t-test vs. Paired samples t-test ]
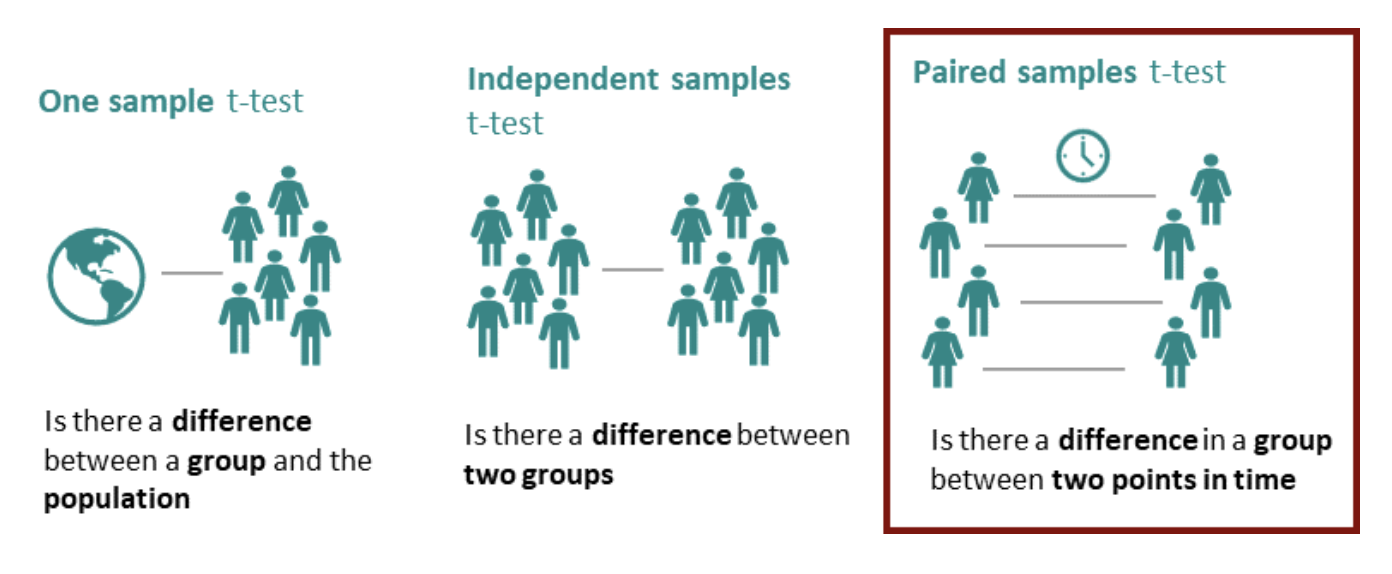
짝을 이룬 t-test(paired t-test)는 종속 표본 t-test (the dependent samples t-test), 짝을 이룬 차이 t-test (the paired-difference t-test), 매칭된 짝 t-test (the matched pairs t-test), 반복측정 표본 t-test (the repeated-sample t-teset) 등의 이름으로도 알려져있습니다. 동일한 객체에 대해서 전과 후로 나누어서 반복 측정을 합니다.
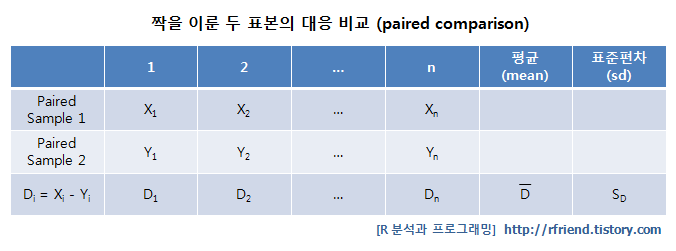
아래의 도표에는 짝을 이룬 두 표본의 대응 비교 데이터셋에 대한 모습입니다. (Xi, Yi) 가 동일한 대상에 대해서 before-after 로 반복 측정되어서, 각 동일 객체의 전-후의 차이 (즉, Di = Xi - Yi) 에 대해서 검정을 진행하게 됩니다.
[ 가정사항 (Assumptions) ]
(1) 측정 대상이 독립적(independent)이어야 합니다. 하나의 객체에 대한 측정은 어떤 다른 객체의 측정에 영향을 끼치지 않아야 합니다.
(2) 각 짝을 이룬 측정치는 동일한 객체로 부터 얻어야 합니다. 예를 들면, 신약의 효과를 알아보기 위해 투약 전-후(before-after) 를 측정할 때 동일한 환자에 대해서 측정해야 합니다.
(3) 짝을 이뤄 측정된 전-후의 차이 값은 정규분포를 따라야한다는 정규성(normality) 가정이 있습니다. 만약 정규성 가정을 충족시키지 못하면 비모수 검정(nonparametric test) 방법을 사용해야 합니다.
[ (예제) 신약 치료 효과 여부 검정 ]
새로운 당뇨병 치료제를 개발한 제약사의 예를 계속 들자면, 치료에 지대한 영향을 주는 외부요인을 통제하기 위해 10명의 당뇨병 환자를 선별하여 1달 동안 '위약(placebo)'을 투여한 기간의 혈당 (Xi)과 동일 환자에게 '신약(new medicine)'을 투여한 1달 기간 동안의 혈당 수치(Yi)를 측정하여 짝을 이루어 혈당 차이를 유의수준 5%에서 비교하는 방법이 짝을 이룬 표본에 대한 검정이 되겠습니다. (palacebo 와 신약 투여 순서는 무작위로 선정. 아래 예는 그냥 예시로 아무 숫자나 입력해본 것임. 혈당 수치 이런거 전 잘 몰라요. ^^;)
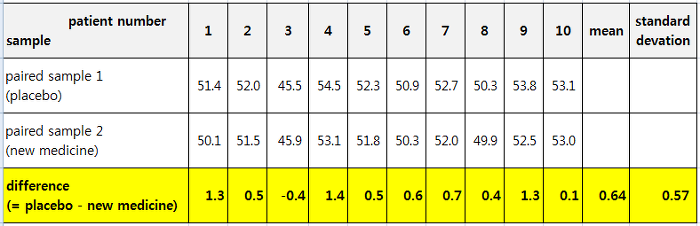
* 귀무가설 (Null Hypothesis, H0): 신약 투입 효과가 없다 (Mu1 = Mu2, ie. Difference=0)
* 대립가설 (Alternative Hypothesis, H1): 신약 투입 효과가 있다 (Mu1 > Mu2, ie. Difference > 0, right-sided test)
[ Python scipy 모듈을 이용한 paired t-test 실행 ]
scipy 모듈의 scipy.stats.ttest_rel 메소드를 사용해서 쌍을 이룬 t-test 를 실행합니다. "Calculate the t-test on TWO RELATED samples of scores, a and b." 라는 설명처럼 TWO RELATED samples 에서 rel 을 타서 메소드 이름을 지었습니다. (저라면 ttest_paired 라고 메소드 이름 지었을 듯요...)
alternative='two-sided' 가 디폴트 설정인데요, 이번 예제에서는 'H1: 신약이 효과가 있다. (즉, 신약 먹기 전보다 신약 먹은 후에 혈당이 떨어진다)' 는 가설을 검정하기 위한 것이므로 alternative='greater' 로 설정을 해주었습니다.
## -- Paired t-test
import numpy as np
from scipy import stats
## sample data-set (repeated measurements of Before vs. After for the same objects)
bef = np.array([51.4, 52.0, 45.5, 54.5, 52.3, 50.9, 52.7, 50.3, 53.8, 53.1])
aft = np.array([50.1, 51.5, 45.9, 53.1, 51.8, 50.3, 52.0, 49.9, 52.5, 53.0])
## paired t-test using Python scipy module
# H0: New medicine is not effective (i.e., no difference b/w before and after)
# H1: New medicine is effective (i.e., there is difference b/w before and after)
stat, p_val = stats.ttest_rel(bef, aft, alternative='greater')
print('statistic:', stat, ' p-value:', p_val)
# statistic: 3.550688262985491 p-value: 0.003104595950799298
분석 결과 p-value 가 0.003 으로서 유의수준 0.05 하에서 귀무가설 (H0: 신약은 효과가 없다. 즉, before와 after의 차이가 없다) 을 기각(reject)하고, 대립가설(H1: 신약은 효과가 있다. 즉, before 보다 after의 혈당 수치가 낮아졌다)을 채택(accept) 합니다.
[ Reference ]
* The Paired t-test
: https://www.jmp.com/en_nl/statistics-knowledge-portal/t-test/paired-t-test.html
* scipy.stats.ttest_rel
(Calculate the t-test on TWO RELATED samples of scores, a and b.)
: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)




