지난번 포스팅에서는 시계열 패턴별 지수 평활법 (exponential smoothing by time series patterns) (https://rfriend.tistory.com/511) 에 대해서 소개하였습니다.
이번 포스팅에서는 시계열 자료 예측 모형의 성능, 모델 적합도 (goodness-of-fit of the time series model) 를 평가할 수 있는 지표, 통계량을 알아보겠습니다.
아래의 모델 적합도 평가 지표들의 리스트를 살펴보시면 선형회귀모형의 모델 적합도 평가 지표와 유사하다는 것을 알 수 있습니다.(실제값과 예측값의 차이 또는 설명비율에 기반한 성능 평가라는 측면에서는 동일하며, 회귀모형은 종속변수와 독립변수간 상관관계에 기반한 반면에 시계열 모형은 종속변수와 자기자신의 과거 데이터와의 자기상관관계에 기반한 다는것이 다른점 입니다.)
아래 평가지표들 중에서 전체 분산 중에서 모델이 설명할 수 있는 비율을 나타내는 수정결정계수는 통계량 값이 높을 수록 좋은 모델이며, 나머지 오차에 기반한 평가 지표(통계량)들은 값이 낮을 수록 상대적으로 더 좋은 모델이라고 평가를 합니다. (단, SST는 제외)
이들 각 지표별로 좋은 모델 여부를 평가하는 절대 기준값(threshold)이 있는 것은 아니며, 여러개의 모델 간 성능을 상대적으로 비교 평가할 때 사용합니다.
- 전체제곱합 (SST, total sum of square)
- 오차제곱합 (SSE, error sum of square)
- 평균오차제곱합 (MSE, mean square error)
- 제곱근 평균오차제곱합 (RMSE, root mean square error)
- 평균오차 (ME, mean error)
- 평균절대오차 (MAE, mean absolute error)
- 평균비율오차 (MPE, mean percentage error)
- 평균절대비율오차 (MAPE, mean absolute percentage error)
- 수정결정계수 (Adj. R-square)
- AIC (Akaike's Information Criterion)
- SBC (Schwarz's Bayesian Criterion)
- APC (Amemiya's Prediction Criterion)
[ 시계열 데이터 예측 모형 적합도 평가 지표 (goodness-of-fit measures for time series prediction models) ]

1. 전체제곱합 (SST, total sum of square)
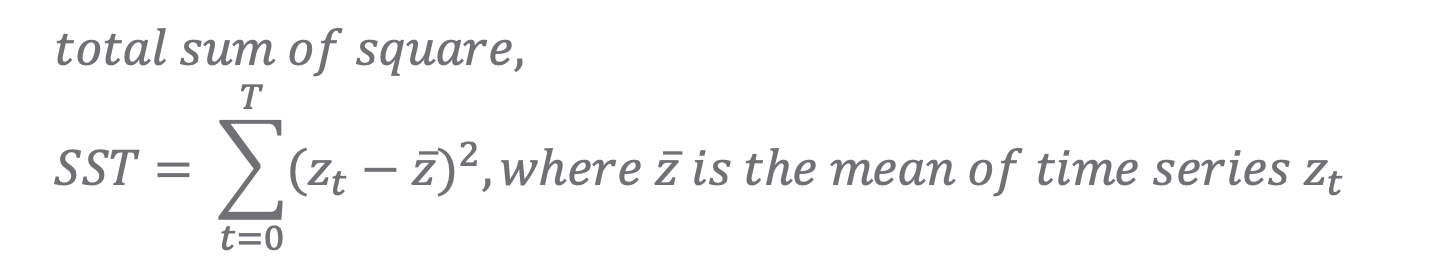
SST는 시계열 값에서 시계열의 전체 평균 값을 뺀 값으로, 시계열 예측 모델을 사용하지 않았을 때 (모든 모수들이 '0' 일 때) 의 오차 제곱 합입니다. 나중에 결정계수(R2), 수정결정계수(Adj. R2)를 계산할 때 사용됩니다. (SST 는 모델 성능 평가에서는 제외)
2. 오차제곱합 (SSE, error sum of square)

3. 평균오차제곱합 (MSE, mean square error), 제곱근 평균오차제곱합 (RMSE, root mean square error)

MSE는 많은 통계 분석 패키지, 라이브러리에서 모델 훈련 시 비용함수(cost function) 또는 모델 성능 평가시 기본 설정 통계량으로 많이 사용합니다.
RMSE (Root Mean Square Error) 는 MSE에 제곱근을 취해준 값으로서, SSE를 제곱해서 구한 MSE에 역으로 제곱근을 취해주어 척도를 원래 값의 단위로 맞추어 준 값입니다.
4. 평균오차 (ME, mean error)

ME(Mean Error) 는 MAE(Mean Absolute Error)와 함께 해석하는 것이 필요합니다. 왜냐하면 큰 오차 값들이 존재한다고 하더라도 ME 값만 볼 경우 + 와 - 값이 서로 상쇄되어 매우 작은 값이 나올 수도 있기 때문입니다. 따라서 MAE 값을 통해 실제값과 예측값 간에 오차가 평균적으로 얼마나 큰지를 확인하고, ME 값의 부호를 통해 평균적으로 과다예측(부호가 '+'인 경우) 혹은 과소예측(부호가 '-'인 경우) 인지를 가늠해 볼 수 있습니다.
5. 평균절대오차 (MAE, mean absolute error)

6. 평균비율오차 (MPE, mean percentage error)

위의 ME와 MAE 는 척도 문제 (scale problem) 을 가지고 있습니다. 반면에 MPE (Mean Percentage Error)와 MAPE (Mean Absolute Percentage Error) 는 0~100%로 표준화를 해주어서 척도 문제가 없다는 특징, 장점이 있습니다. 역시 MAE 와 MAPE 값을 함께 확인해서 해석하는 것이 필요합니다. 0에 근접할 수록 시계열 예측모델이 잘 적합되었다고 평가할 수 있으며, MAE의 부호(+, -)로 과대 혹은 과소예측의 방향을 파악할 수 있습니다.
7. 평균절대비율오차 (MAPE, mean absolute percentage error)

8. 수정결정계수 (Adj. R-square)
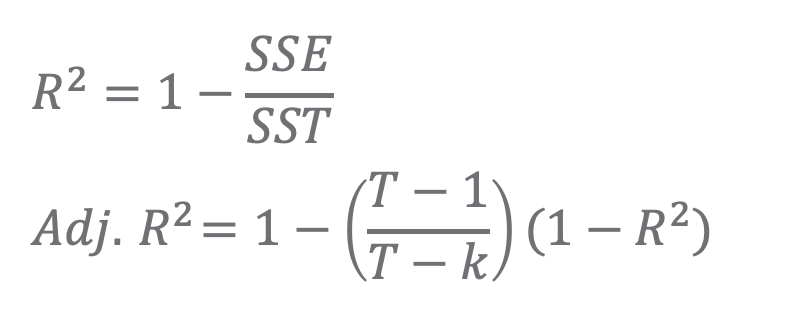
결정계수 R2 는 SST 에서 예측 모델이 설명하는 부분의 비율(R2 = SSR/SST=1-SSE/SST)을 의미합니다. 그런데 결정계수 R2는 모수의 개수가 증가할 수록 이에 비례하여 증가하는 경향이 있습니다. 이러한 문제점을 바로잡기 위해 예측에 기여하지 못하는 모수가 포함될 경우 패널티를 부여해서 결정계수의 값을 낮추어주게 수정한 것이 바로 수정결정계수(Adjusted R2) 입니다. (위의 식에서 k 는 모델에 포함된 모수의 개수를 의미합니다.)
위의 2~7번의 통계량들은 SSE(Error Sum of Square)를 기반으로 하다보니 값이 작을 수록 좋은 모델을 의미하였다면, 8번의 수정결정계수(Adj. R2)는 예측모델이 설명력과 관련된 지표로서 값이 클 수록 더 좋은 모델을 의미합니다.(1에 가까울 수록 우수)
9. AIC, SBC, APC
AIC (Akaike's Information Criterion),
SBC (Schwarz's Bayesian Criterion),
APC (Amemiya's Prediction Criterion)

위의 AIC, SBC, APC 지표들도 SSE(Error Sum of Square) 에 기반한 지표들로서, 값이 작을 수록 더 잘 적합된 모델을 의미합니다. 이들 지표 역시 SSE 를 기본으로 해서 여기에 모델에서 사용한 모수의 개수(k, 패널티로 사용됨), 관측치의 개수(T, 관측치가 많을 수록 리워드로 사용됨)를 추가하여 조금씩 변형을 한 통계량들입니다.
다음번 포스팅에서는 이들 지표를 사용해서 Python으로 하나의 시계열 자료에 대해 여러 개의 지수 평활법 기법들을 적용해서 가장 모형 적합도가 높은 모델을 찾아보겠습니다.(https://rfriend.tistory.com/671)
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요.




