Python의 Dictionary는 {Key: Value}의 쌍(pair)로 이루어진 자료형입니다.
이번 포스팅에서는 Python Dictionary 를 분할하여 새로운 Dictionary로 만드는 방법을 소개하겠습니다.
(1) Dictionary 의 특정 값을 가진 sub Dictionary 만들기
(2) Dictionary 를 특정 비율로 분할하기
먼저 예제로 사용할 Dictionary를 만들어보겠습니다. key 는 영어 알파벳이고, value 는 정수 [0, 1, 2] 중에서 무작위로 생성해서 {key: value} 쌍으로 이루어진 Dictionary 입니다.
# Sample Dictionary
import string
import numpy as np
np.random.seed(1004) # for reproducibility
k = list(string.ascii_lowercase)
v = np.random.randint(3, size=len(k))
my_dict = {k: v for k, v in zip(k, v)}
print(my_dict)
# {'a': 2, 'b': 1, 'c': 2, 'd': 0, 'e': 1, 'f': 2, 'g': 1,
# 'h': 1, 'i': 0, 'j': 0, 'k': 0, 'l': 0, 'm': 0, 'n': 2,
# 'o': 2, 'p': 0, 'q': 2, 'r': 0, 's': 2, 't': 1, 'u': 0,
# 'v': 1, 'w': 0, 'x': 2, 'y': 0, 'z': 2}
(1) Dictionary 의 특정 값을 가진 sub Dictionary 만들기
먼저 my_dict 내 원소의 value 가 각각 0, 1, 2 인 sub Dictionary 를 만들어보겠습니다.
my_dict.items() 로 Dictionary 내 원소 값을 불러오고, 조건절이 있는 list comprehension 을 이용하였으며, for loop 순환문을 사용해도 됩니다.
# (1) Split a Dictionary by each value categories of 0, 1, 2
dict_0 = {k: v for k, v in my_dict.items() if v == 0}
dict_1 = {k: v for k, v in my_dict.items() if v == 1}
dict_2 = {k: v for k, v in my_dict.items() if v == 2}
print('Dict 0:', dict_0)
print('Dict 1:', dict_1)
print('Dict 2:', dict_2)
# Dict 0: {'d': 0, 'i': 0, 'j': 0, 'k': 0, 'l': 0, 'm': 0, 'p': 0, 'r': 0, 'u': 0, 'w': 0, 'y': 0}
# Dict 1: {'b': 1, 'e': 1, 'g': 1, 'h': 1, 't': 1, 'v': 1}
# Dict 2: {'a': 2, 'c': 2, 'f': 2, 'n': 2, 'o': 2, 'q': 2, 's': 2, 'x': 2, 'z': 2}
(2) Dictionary 를 특정 비율로 분할하기

이제 위에서 생성한 sub Dictionary를 먼저 무작위로 순서를 재정렬한 후에, [training : validation : test] = [0.6 : 0.2 : 0.2] 의 비율로 분할을 해보겠습니다.
list(dict_k.keys()) 로 각 sub Dictionary 의 key 값을 리스트로 만든 후에, random.shuffle(keys_list) 로 key 값을 무작위로 순서를 재정렬해주었습니다.
그 후에 [train:validation:test] = [0.6:0.2:0.2] 의 비율에 해당하는 각 sub Dictionary의 원소값의 개수를 계산한 후에, 이 원소 개수만큼 keys_list 에서 key 값 리스트를 indexing 해 옵니다.
그리고 마지막으로 list comprehension을 이용해서 train, validation, test set 별 key 해당하는 value 를 가져와서 {key: value} 쌍으로 train/validation/test set의 각 Dictionary를 만들어주면 됩니다.
# (2) Split each Dictionary into training set 60%, validation 20%, test set 20% randomly
def split_dict(dict_k, train_r=0.6, val_r=0.2, verbose=False):
import random
random.seed(1004)
keys_list = list(dict_k.keys())
# randomize the order of the keys
random.shuffle(keys_list)
# numbers per train, validation, and test set
num_train = int(len(keys_list) * train_r)
num_val = int(len(keys_list) * val_r)
# split kyes
keys_train = keys_list[:num_train] # 60%
keys_val = keys_list[num_train:(num_train+num_val)] # 20%
keys_test = keys_list[(num_train+num_val):] # 20% = 1 - train_ratio - val_ratio
# split a Dictionary
dict_k_train = {k: dict_k[k] for k in keys_train}
dict_k_val = {k: dict_k[k] for k in keys_val}
dict_k_test = {k: dict_k[k] for k in keys_test}
if verbose:
print('Keys List:', keys_list)
print('---' * 20)
print('Training set:', dict_k_train)
print('Validation set:', dict_k_val)
print('Test set:', dict_k_test)
return dict_k_train, dict_k_val, dict_k_test
실제로 dict_0, dict_1, dict_2 의 각 sub Dictionary에 위에서 정의한 사용자 정의 함수 split_dict() 함수를 적용해보겠습니다.
## (a) split dict_0
dict_0_train, dict_0_val, dict_0_test = split_dict(
dict_0,
train_r=0.6,
val_r=0.2,
verbose=True
)
# Keys List: ['m', 'r', 'l', 'd', 'j', 'w', 'y', 'k', 'u', 'i', 'p']
# ------------------------------------------------------------
# Training set of Dict 0: {'m': 0, 'r': 0, 'l': 0, 'd': 0, 'j': 0, 'w': 0}
# Validation set of Dict 0: {'y': 0, 'k': 0}
# Test set of Dict 0: {'u': 0, 'i': 0, 'p': 0}
## (b) split dict_1
dict_1_train, dict_1_val, dict_1_test = split_dict(
dict_1,
train_r=0.6,
val_r=0.2,
verbose=True
)
# Keys List: ['g', 'v', 't', 'e', 'b', 'h']
# ------------------------------------------------------------
# Training set: {'g': 1, 'v': 1, 't': 1}
# Validation set: {'e': 1}
# Test set: {'b': 1, 'h': 1}
## (c) split dict_2
dict_2_train, dict_2_val, dict_2_test = split_dict(
dict_2,
train_r=0.6,
val_r=0.2,
verbose=True
)
# Keys List: ['f', 'n', 'a', 'x', 'z', 'o', 'q', 'c', 's']
# ------------------------------------------------------------
# Training set of Dict 0: {'m': 0, 'r': 0, 'l': 0, 'd': 0, 'j': 0, 'w': 0}
# Validation set of Dict 0: {'y': 0, 'k': 0}
# Test set of Dict 0: {'u': 0, 'i': 0, 'p': 0}
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)

'Python 분석과 프로그래밍 > Python 데이터 전처리' 카테고리의 다른 글
| [Python pandas] 리스트를 행으로 변환하여 DataFrame 만들기 (0) | 2023.08.14 |
|---|---|
| [Python] 리스트와 사전 자료형을 이용해서 문자열과 숫자 매핑하기 (0) | 2023.07.16 |
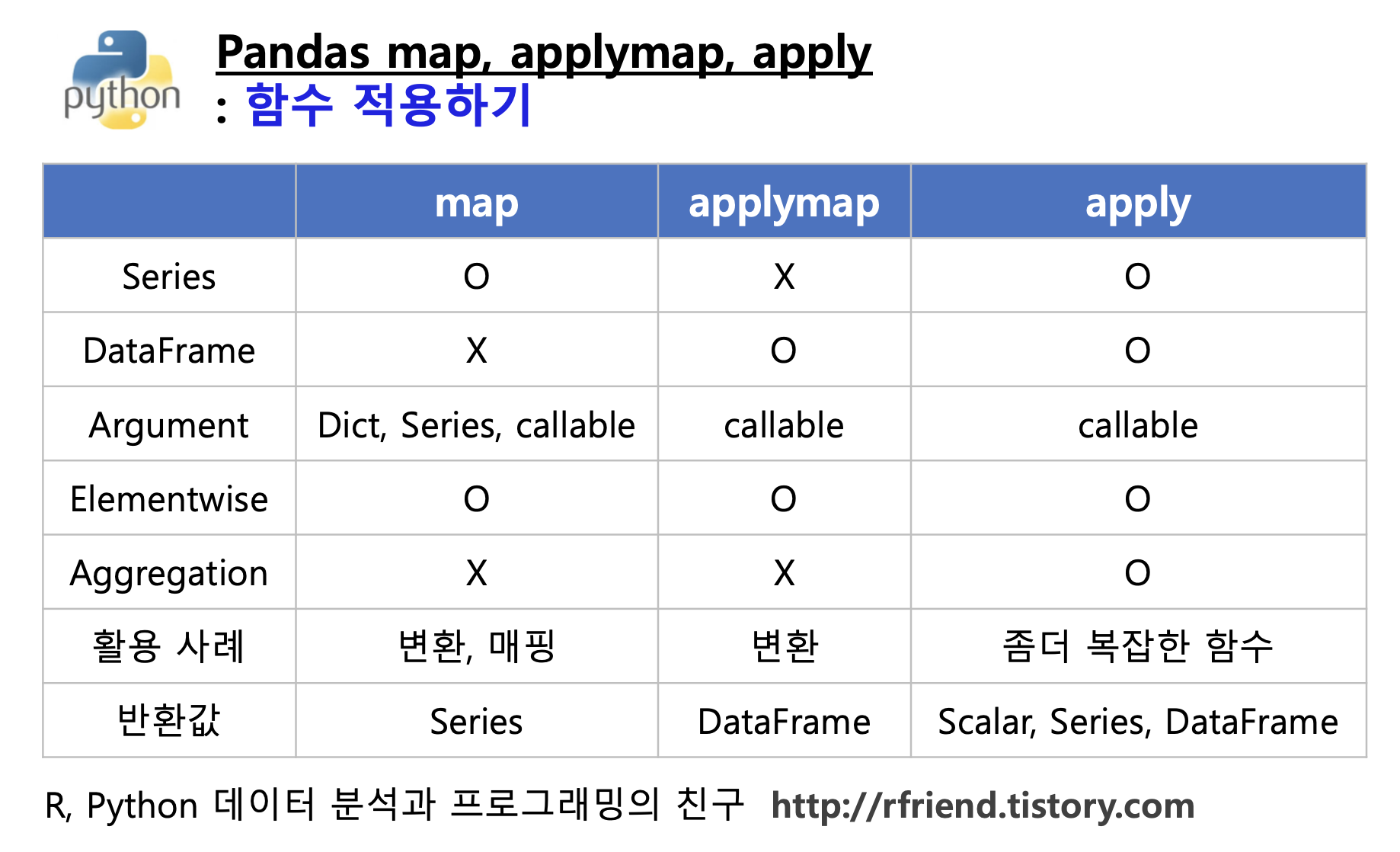
| [Python] Pandas 함수 적용: map(), applymap(), apply() (0) | 2023.06.06 |
| [Python] 파워포인트와 PDF 파일에서 텍스트 추출하기 (0) | 2023.03.19 |
| [Python Numpy] 반복자 enumerate() vs. 다차원 반복자np.ndenumerate() (0) | 2023.03.05 |