[Python] Python을 이용한 분류 모델 성능 평가 (classification model evaluation using Python)
Python 분석과 프로그래밍/Python 기계학습 2023. 1. 24. 21:00지난번 포스팅에서는 분류 모델(classification model)의 성능을 평가할 수 있는 지표 (evaluation metrics)에 대해서 소개하였습니다. (https://rfriend.tistory.com/771)
이번 포스팅에서는 Python을 사용하여 예제 데이터에 대해 분류 모델의 성능 평가를 해보겠습니다.
(1) 예제로 사용할 Breast Cancer 데이터셋을 로딩하고, Data와 Target으로 구분
(2) Training set, Test set 분할
(3) Logistic Regression 모델 적합 (Training)
(4) 예측 (Prediction)
(5) 혼돈 매트릭스 (Confusion Matrix)
(6) 분류 모델 성능 지표: Accuracy, Precision, Recall rate, Specificity, F-1 score
(7) ROC 곡선, AUC 점수
(1) 예제로 사용할 Breast Cancer 데이터셋을 로딩하고, Data와 Target으로 구분
target의 '0' 이 'malignant (악성 종양)' 이고, '1'은 'benign' 으로서 정상을 의미합니다. 우리는 'malignant (악성 종양)' 을 분류하는 모델에 관심이 있으므로 target '0' 이 'Positive Label' 이 되겠습니다.
import numpy as np
## load a Iris dataset
from sklearn.datasets import load_breast_cancer
bc = load_breast_cancer()
## target names
bc.target_names
#array(['malignant', 'benign'], dtype='<U9')
## [0: 'malignant'(악성), 1: 'benign']
np.unique(bc['target'], return_counts=True)
#(array([0, 1]), array([212, 357]))
## getting data, target
bc_data = bc['data']
bc_target = bc['target']
bc_data.shape
#(569, 30)
bc_target[:20]
#array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1])
(2) Training set, Test set 분할
Training set 0.5, Test set 0.5 의 비율로 무작위 추출하여 분할하였습니다.
## splits training and test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
bc_data,
bc_target,
test_size=0.5,
random_state=1004
)
(3) Logistic Regression 모델 적합 (Training)
Traning set을 사용해서 로지스틱 회귀모형을 적합하였습니다.
## training a Logistic Regression model with training set
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(
solver='liblinear',
random_state=1004).fit(X_train, y_train)
(4) 예측 (Prediction)
Test set에 대해서 예측을 하고 모델 성능 평가를 해보겠습니다.
predict() 메소드는 범주를 예측하여 반환하고, predict_praba() 메소드는 확률(probability)을 반환합니다.
## prediction for test set
y_pred = clf.predict(X_test) # class
y_pred_proba = clf.predict_proba(X_test) # probability
실제 범주의 값과 예측한 범주의 값, 그리고 target '0'(malignant, 악성 종양) 일 확률을 DataFrame으로 묶어보았습니다.
# All in a DataFrame
pred_df = pd.DataFrame({
'actual_class': y_test,
'predicted_class': y_pred,
'probabilty_class_0': y_pred_proba[:,0] # malignant (악성)
})
pred_df.head(10)
# actual_class predicted_class probabilty_class_0
# 0 1 1 0.002951
# 1 0 0 0.993887
# 2 0 1 0.108006
# 3 1 1 0.041777
# 4 0 0 1.000000
# 5 0 0 1.000000
# 6 0 0 0.999633
# 7 1 1 0.026465
# 8 0 0 0.997405
# 9 1 1 0.002372
이제 여기서부터 분류 모델의 성능 평가를 시작합니다.
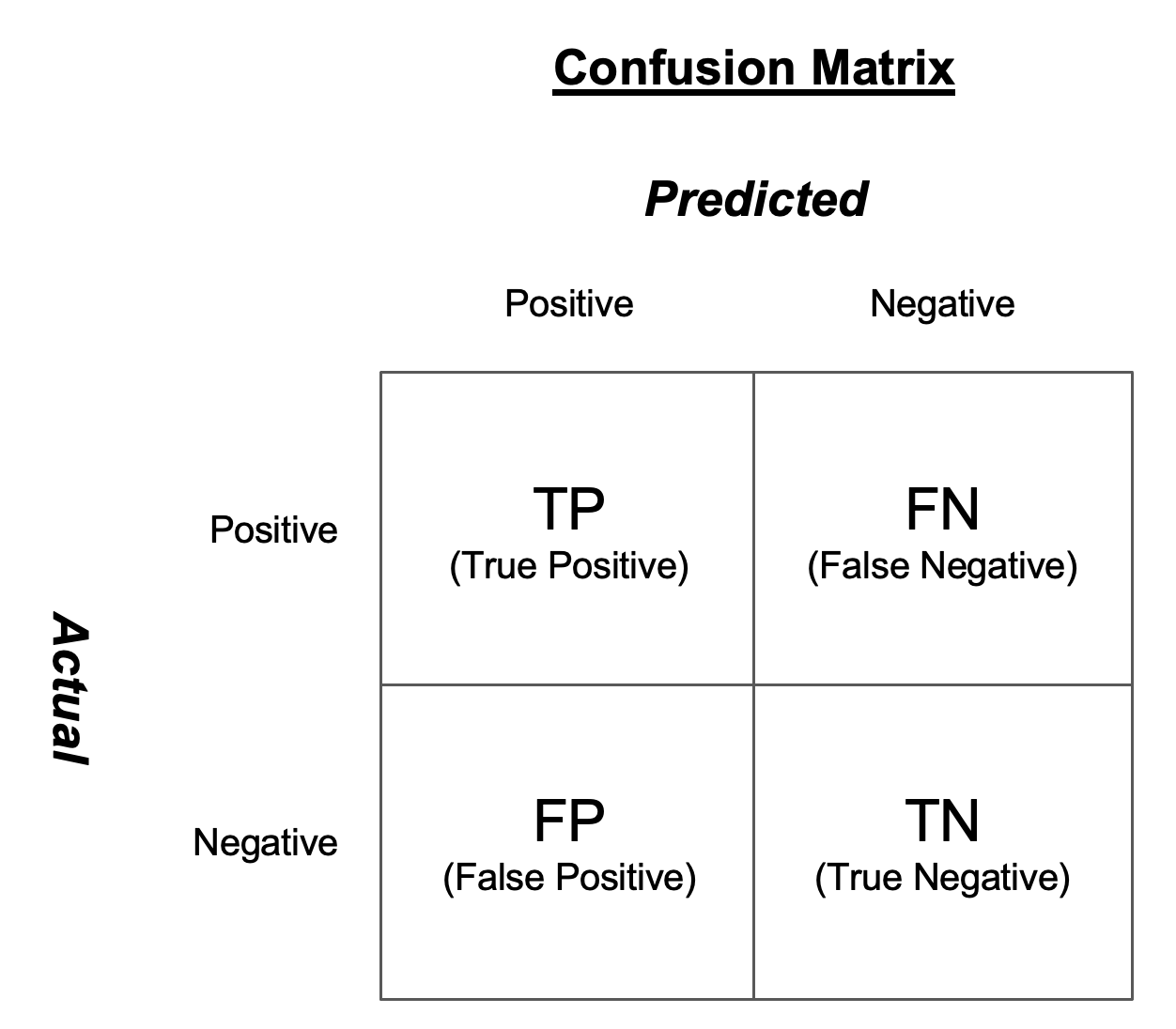
(5) 혼돈 매트릭스 (Confusion Matrix)
혼돈 매트릭스의 Y축은 Actual 의 malignant (0), benign(1) 이며, X 축은 Predicted 의 malignant (0), benign(1) 입니다.
## model evaluation
# Confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred,
labels=[0, 1]) # 'malignant'(0), 'benign'(1)
# predicted
# malignant benign
# actual malignant [[102, 16],
# benign [ 3, 164]])
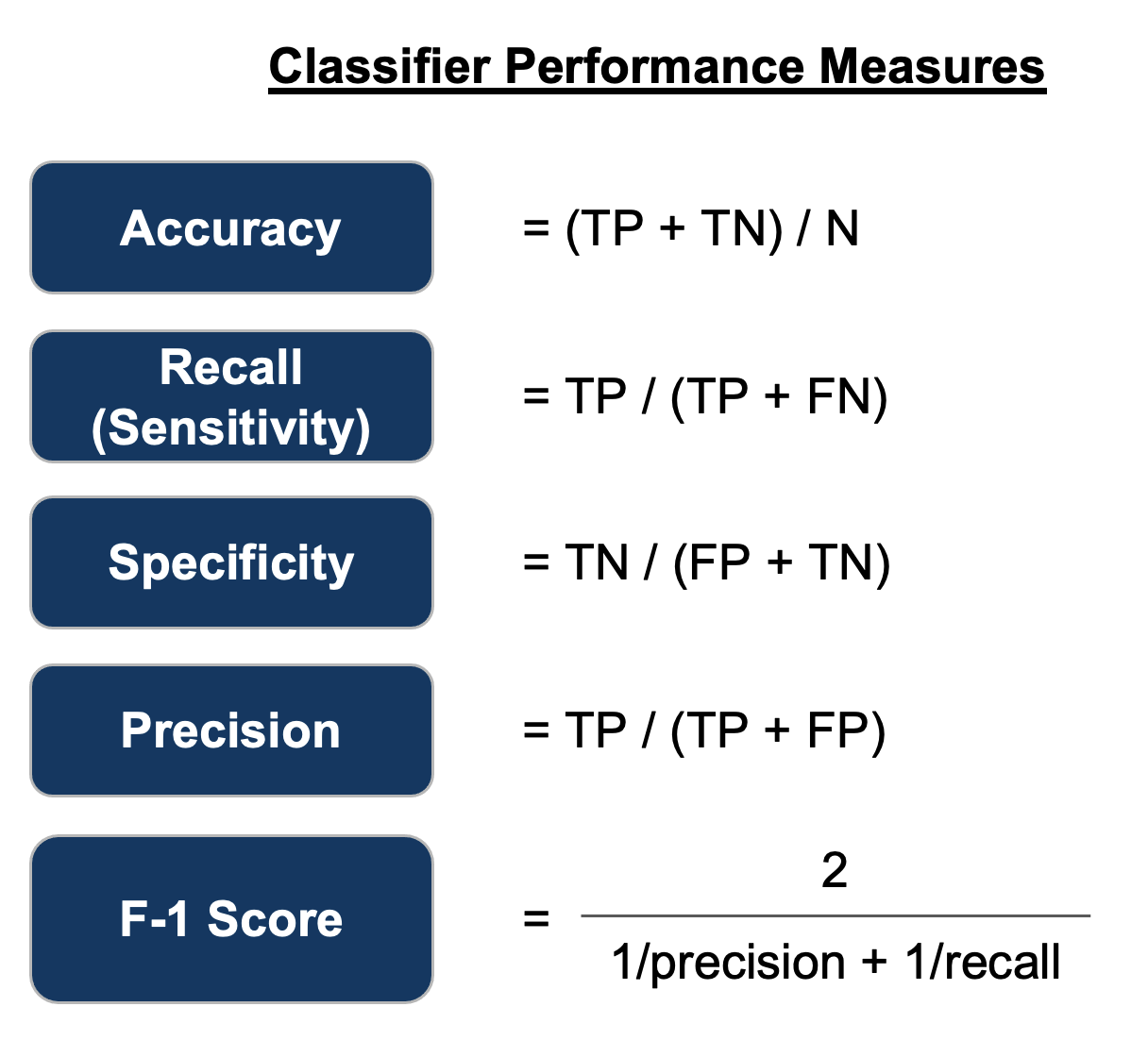
(6) 분류 모델 성능 지표: Accuracy, Precision, Recall rate, Specificity, F-1 score
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_recall_fscore_support
## performance metrics
accuracy = accuracy_score(y_test, y_pred)
precision, recall, fscore, support = \
precision_recall_fscore_support(y_test, y_pred)
print('Accuracy : %.3f' %accuracy) # (102+164)/(102+16+3+164)
print('Precision : %.3f' %precision[0]) # 102/(102+3)
print('Recall : %.3f' %recall[0]) # 102/(102+16)
print('Specificyty: %.3f' %recall[1]) # 164/(3+164)
print('F1-Score : %.3f' %fscore[0]) # 2/(1/precision + 1/recall) = 2/(1/0.971+1/0.864)
# Accuracy : 0.933
# Precision : 0.971
# Recall : 0.864
# Specificyty: 0.982
# F1-Score : 0.915
sklearn의 classification_report() 메소드를 활용해서 한꺼번에 쉽게 위의 분류 모델 성능평가 지표를 계산하고 출력할 수 있습니다. 참고로, 'macro avg' 는 가중치가 없는 평균이며, 'weighted avg'는 support (관측치 개수) 로 가중치를 부여한 평균입니다.
from sklearn.metrics import classification_report
target_names = ['malignant(0)', 'benign(1)']
print(classification_report(y_test, y_pred,
target_names=target_names))
# precision recall f1-score support
# malignant(0) 0.97 0.86 0.91 118
# benign(1) 0.91 0.98 0.95 167
# accuracy 0.93 285
# macro avg 0.94 0.92 0.93 285
# weighted avg 0.94 0.93 0.93 285
(7) ROC 곡선, AUC 점수
ROC 곡선과 AUC 점수는 예측 확률을 이용합니다.
ROC 곡선은 모든 의사결정 기준선 (decision threshold)에 대하여 혼돈 매트릭스를 만들고, X축에는 False Positive Rate(=1-specificity), Y축에는 True Positive Rate (=recall, sensitivity) 의 값을 선그래프로 그린 것이며, 좌측 상단으로 그래프가 붙을 수록 더 잘 적합된 모델이라고 평가합니다. AUC 점수는 ROC 곡선의 아랫부분의 면적을 적분한 값입니다.
## ROC Curve, AUC
import sklearn.metrics as metrics
fpr, tpr, threshold = metrics.roc_curve(
y_test,
y_pred_proba[:, 0],
pos_label=0) # positive label
AUC = metrics.auc(fpr, tpr)
# plotting ROC Curve
import matplotlib.pyplot as plt
plt.figure(figsize = (8, 8))
plt.plot(fpr, tpr, 'b', label = 'AUC = %0.3f' % AUC)
plt.title(('ROC Curve of Logistic Regression'), fontsize=18)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],'r--') # random guess
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate',
fontsize=14)
plt.xlabel('False Positive Rate',
fontsize=14)
plt.show()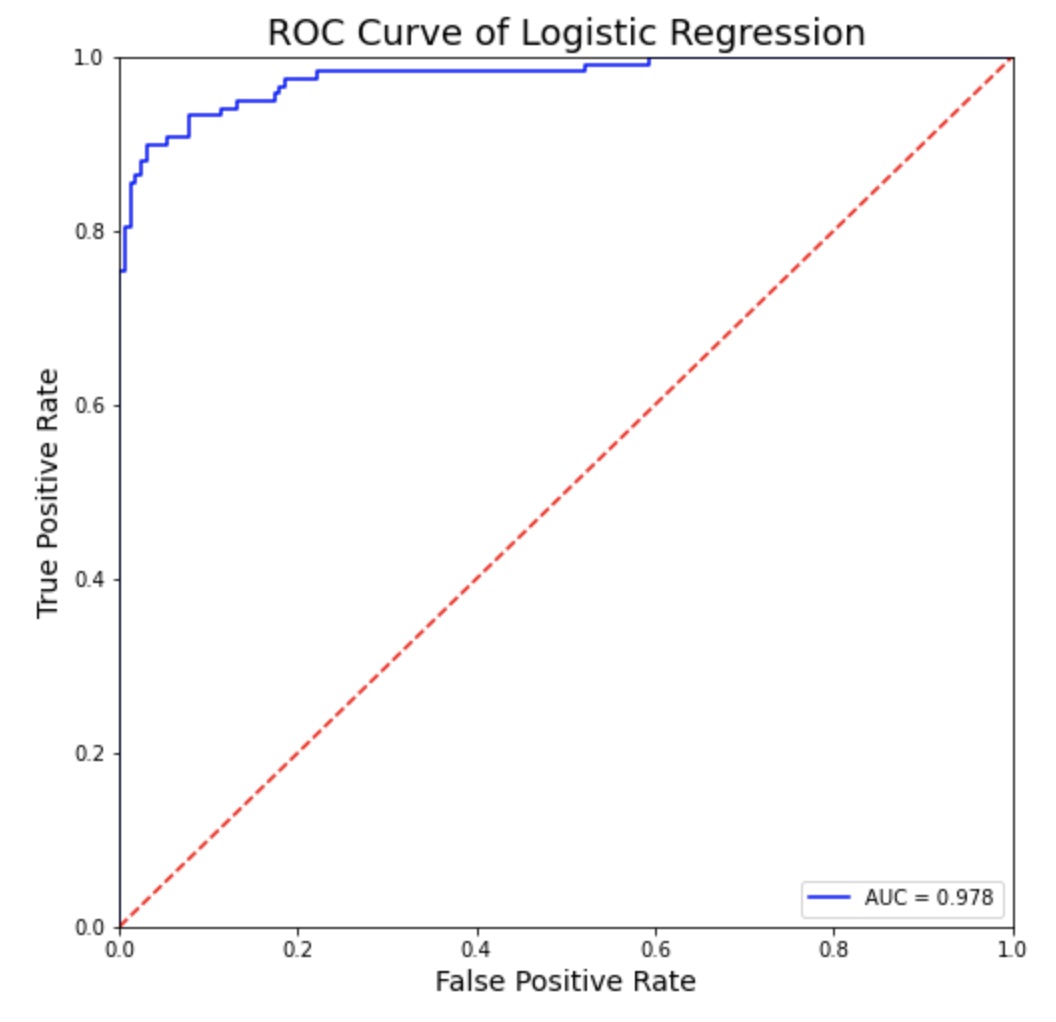
[ Reference ]
1) Breast Cancer Dataset
: https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_breast_cancer.html
2) Scikit-Learn Logistic Regression
: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
3) 분류 모델의 성과 평가 지표 : https://rfriend.tistory.com/771
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)




