[시계열 분석] Drift, Shift 는 무엇이고, 어떻게 분석하는가?
"Drift"와 "Shift"는 시계열 데이터 분석에서 중요한 두 가지 개념이며, 시간에 따른 데이터의 다양한 변화 또는 변동을 나타냅니다.
이번 포스팅에서는
1. 시계열 데이터의 Drift 란 무엇인가?
2. 시계열 데이터의 Shift 란 무엇인가?
3. 시계열 데이터의 Drift와 Shift 분석은 어떻게 하나?
4. Python 을 이용한 시계열 데이터 Drift, Shift 생성/ 시각화 및 탐지 예시
에 대해서 소개하겠습니다.

1. 시계열 데이터에서의 Drift 란 무엇인가?
- 정의: Drift 는 시계열 데이터가 시간에 따라 느리고 점진적이며 종종 선형적으로 변화는 것(a slow, gradual, and often linear change in the time series data over time)을 의미합니다. 이는 한 방향으로 지속적인 변화 경향, 즉 상승 또는 하락하는 경향입니다.
- 예시: 재무 데이터에서, 주식 가치가 몇 년 동안 지속적으로 상승하거나 하락하는 경우, 이는 드리프트의 예입니다.
- 중요성: 드리프트를 이해하고 식별하는 것은 정확한 예측 및 장기적인 추세를 반영하는 모델을 만드는 데 중요합니다. 드리프트를 무시하면 시간이 지남에 따라 점점 더 부정확해지는 모델이 될 수 있습니다.
2. 시계열 데이터에서의 Shift 란 무엇인가?
- 정의: Shfit, 종종 "레벨 시프트(level shift)"로 언급되며, 시계열의 평균 또는 분산에서 갑작스러운 변화 (a sudden change in the mean or variance of a time series)를 의미합니다. 드리프트와 달리, 시프트는 갑작스럽게 발생하며 언제든지 일어날 수 있습니다.
- 유형: 평균 시프트 (Mean Shift)와 분산 시프트 (Variance Shift) 로 나누어볼 수 있습니다.
-. 평균 시프트 (Mean Shift): 시리즈의 평균 수준이 갑자기 변경되는 경우입니다. 예를 들어, 성공적인 마케팅 캠페인으로 인해 판매량이 갑자기 증가하는 경우가 이에 해당합니다.
-. 분산 시프트 (Variance Shift): 시리즈의 변동성이 변경되는 경우입니다, 예를 들어 주식 가격의 변동성 증가와 같은 경우입니다.
- 중요성: 시프트를 감지하는 것은 시계열 데이터에서 갑작스러운 변화를 이해하고 대응하는 데 필수적입니다. 시프트는 중대한 사건, 시스템의 구조적 변화 또는 데이터에 영향을 미치는 외부 요인의 변화를 나타낼 수 있습니다.
3. 시계열 데이터의 Drift와 Shift 분석은 어떻게 하나?
시계열 데이터에서 드리프트와 시프트를 분석하는 것은 시간이 지남에 따라 데이터에서 점진적인 (Drift) 및 급격한 (Shift) 변화를 식별하고 정량화하는 것을 포함합니다. 이 목적을 위해 다양한 방법과 알고리즘이 사용되며, 각각은 데이터 유형과 분석 요구 사항에 적합합니다. 여기에 주요한 몇 가지를 소개합니다.
3-1. 통계적 공정 관리 방법 (SPC, Statistical Process Control)
- 제어 차트 (Control Charts): 평균 또는 분산의 변화를 탐지하기 위해 CUSUM (Cumulative Sum Control Chart) 및 EWMA(Exponentially Weighted Moving Average)와 같은 차트가 사용됩니다. 품질 관리에서 널리 사용됩니다.
- Shewhart 제어 차트 (Shewhart Control Charts): 큰 시프트는 감지할 수 있지만 작은 시프트나 드리프트에는 덜 민감합니다.
3-2. 시계열 분석 방법 (Time Series Analysis Methods)
- 이동 평균(Moving Average): 단기 변동을 평활화하고 장기 추세나 주기(long-term trends or cycles)를 강조하는 데 도움이 됩니다.
- 시계열 분해 방법 (Time Series Decomposition Methods): STL (Seasonal and Trend decomposition using Loess)과 같은 기술은 시계열을 추세(Trend), 계절성(Seasonality) 및 잔차(Residual) 요소로 분해하여 드리프트와 시프트를 식별하는 데 도움이 됩니다.
3-3. 변화점 감지 알고리즘 (Change Point Detection Algorithms)
- Bai-Perron 검정: 선형 모델에서 여러 중단점을 감지하는 데 사용됩니다.
- 변화점 분석 (Changepoint Analysis): PELT (Pruned Exact Linear Time), 이진 분할 (Binary Segmentation), 세그먼트 이웃 (Segment Neighborhoods)과 같은 방법은 대규모 데이터셋에서 다중 변화점을 감지하도록 설계되었습니다.
- CUSUM (Cumulative Sum Control Chart) 및 EWMA (Exponentially Weighted Moving Average): 평균 또는 분산의 변화를 식별하는 변화점 감지에 적응할 수 있습니다.
3-4. 기계 학습 접근 방식
- 지도 학습 (Supervised Learning): 변화점 전후를 나타내는 레이블이 있는 데이터가 있을 경우, 변화점을 감지하기 위해 기계 학습 모델을 훈련할 수 있습니다.
- 비지도 학습 (Unsupervised Learning): 클러스터링(예: k-means clustering, DBSCAN)과 같은 기술은 데이터 분포의 변화를 감지하여 시프트를 식별하는 데 사용될 수 있습니다.
3-5. 신호 처리 기술 (Signal Processing Techniques)
- 푸리에 변환 (Fourier Transform): 주파수 영역의 시프트를 식별하는 데 유용합니다.
- 웨이블릿 변환 (Wavelet Transform): 비정상 시계열에서 급격한 및 점진적인 변화를 모두 감지하는 데 효과적입니다.
3-6. 베이지안 방법 (Bayesia Methods)
- 베이지안 실시간 변화점 감지 (Bayesian Online Change Point Detection): 실시간 데이터 스트림에서 변화점을 감지하는 데 유용한 확률적 접근 방식입니다.
3-7. 계량경제학에서의 구조적 분석 검정
- Dickey-Fuller 검정: 시계열 샘플에서 단위근을 테스트하는 데 사용되며, 이는 종종 드리프트의 징후입니다.
- Chow 검정: 특정 시점에서 구조적 중단이 있는지 여부를 결정하기 위해 설계되었습니다.
3-8. 회귀 기반 방법 (Regression-based Methods)
- 선형 회귀 (Linear Regression): 기울기 계수 (slope coefficient)를 평가하여 드리프트를 탐지할 수 있습니다.
- 분할 회귀 (Segmented Regression): 알려지지 않은 시점에서 회귀 모델의 변화를 탐지하는 데 유용합니다.
적용 방법은 데이터의 특성 (노이즈 수준, 샘플 크기, 계절성 존재 여부 등)과 분석 요구 사항 (실시간 감지, 작은 변화에 대한 민감도 등)에 따라 다릅니다. 실제로 이러한 방법들의 조합이 종종 사용되어 결과를 검증하고 시계열 데이터에 대한 종합적인 이해를 얻습니다.
요약하자면, Drift와 Shift 분석은 시계열 데이터에서의 변화가 점진적인지 또는 갑작스러운지를 이해하는 데 도움이 됩니다. 이러한 이해는 시계열 데이터를 기반으로 한 정확한 모델링, 예측 및 의사결정에 있어 중요합니다.
4. Python 을 이용한 시계열 데이터 Drift, Shift 생성/ 시각화 및 탐지 예시
4-1. Python을 이용한 시계열 데이터 Drift, Mean Shift, Variance Shift 생성/ 시각화
## Creating a time series with Drift, Mean Shift, Variance Shift
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Setting a seed for reproducibility
np.random.seed(1004)
# (1) Creating a time series with drift
time = np.arange(100)
drift = 0.5 * time # Linear drift, Trend
noise = np.random.normal(0, 0.5, 100)
time_series_drift = drift + noise
# (2) Creating a time series with Mean Shift
shift_point = 50
time_series_mean_shift = np.random.normal(0, 0.5, 100)
time_series_mean_shift[shift_point:] += 10 # Adding a shift at the midpoint
# (3) Creating a time series with Variance Shift
first_variance = 0.5
second_variance = 5
time_series_first = np.random.normal(0, first_variance, 50)
time_series_second = np.random.normal(0, second_variance, 50)
time_series_var_shift = np.concatenate((time_series_first, time_series_second), axis=0)
# Plotting the time series
plt.figure(figsize=(8, 12))
plt.subplot(3, 1, 1)
plt.plot(time, time_series_drift)
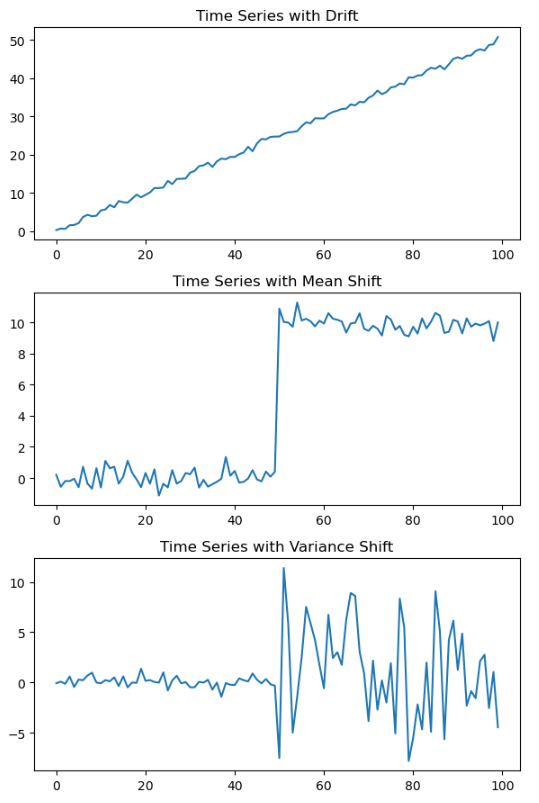
plt.title("Time Series with Drift")
plt.subplot(3, 1, 2)
plt.plot(time, time_series_mean_shift)
plt.title("Time Series with Mean Shift")
plt.subplot(3, 1, 3)
plt.plot(time, time_series_var_shift)
plt.title("Time Series with Variance Shift")
plt.tight_layout()
plt.show()
4-2. Python 으로 회귀모형 기반 Drift 분석
## Analysis of Time Series Drift using Linear Regression Model
from sklearn.linear_model import LinearRegression
# Reshape data for sklearn
X = time.reshape(-1, 1)
y = time_series_drift
# Linear regression
model = LinearRegression()
model.fit(X, y)
# Slope coefficients
print('---' * 10)
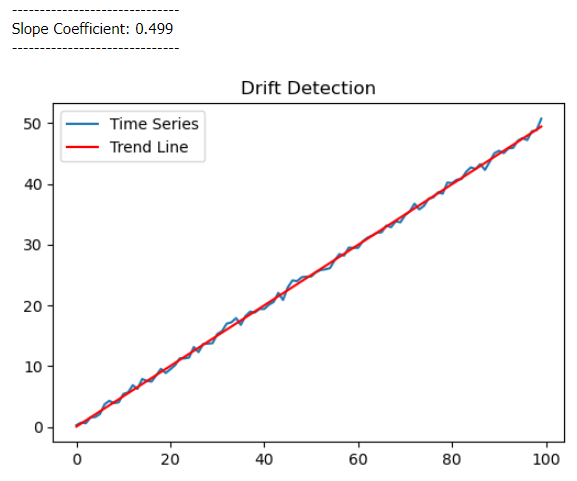
print(f'Slope Coefficient: {model.coef_[0]:.3f}')
print('---' * 10)
# Predicted trend line
trend_line = model.predict(X)
# Plotting
plt.figure(figsize=(6, 4))
plt.plot(time, time_series_drift, label='Time Series')
plt.plot(time, trend_line, label='Trend Line', color='red')
plt.title("Drift Detection")
plt.legend()
plt.show()
4-3. Python으로 시계열 Shift 분석
- Mean Shift 탐지
# Detect Mean Shift
def detect_mean_shift(series, window=5):
for i in range(window, len(series) - window):
before = series[i-window:i]
after = series[i:i+window]
if np.abs(np.mean(after) - np.mean(before)) > 9: # Threshold for shift
return i
return None
mean_shift_point_detected = detect_mean_shift(time_series_mean_shift)
print("----" * 10)
print(f"Mean Shift detected at point: {mean_shift_point_detected}")
print("----" * 10)
# ----------------------------------------
# Shift detected at point: 50
# ----------------------------------------
- PELT (Pruned Exact Linear Time), Binary Segment 알고리즘을 이용한 변곡점 탐지
##-- install "ruptures" module at terminal
!pip install ruptures
## -- change point detection using PELT (Pruned Exact Linear Time) Algorithm
# Specify the PELT model and fit it to the data
model = "l2" # Change to "rbf" for the radial basis function cost model
algo = rpt.Pelt(model=model).fit(time_series_mean_shift)
# Retrieve the change points
result = algo.predict(pen=10) # Adjust the penalty value as needed
# Print the detected change points
print("Change points:", result)
# Change points: [50, 100]
## -- change point detection using Binary Segmentation Algorithm
# Specify the Binary Segment model and fit it to the data
model = "l2" # Change to "rbf" for the radial basis function cost model
algo = rpt.Binseg(model=model).fit(time_series_mean_shift)
# Retrieve the change points
result = algo.predict(pen=10) # Adjust the penalty value as needed
# Print the detected change points
print("Change points:", result)
# Change points: [50, 100]
- Variance Shift 탐지
# Detect Variance Shift
def detect_var_shift(series, window=5):
for i in range(window, len(series) - window):
before = series[i-window:i]
after = series[i:i+window]
if np.abs(np.var(after) - np.var(before)) > 30: # Threshold for shift
return i + int(window/2) + 1
return None
var_shift_point_detected = detect_var_shift(time_series_var_shift)
print("----" * 10)
print(f"Variance Shift detected at point: {var_shift_point_detected}")
print("----" * 10)
# ----------------------------------------
# Variance Shift detected at point: 50
# ----------------------------------------
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요! :-)

