[LangChain] RecursiveUrlLoader 를 사용하여 Root directory 밑의 모든 URL 텍스트 데이터 가져오기
Deep Learning (TF, Keras, PyTorch)/Natural Language Processing 2024. 1. 9. 23:50데이터, 정보가 저장되고 공유되고 유통되는 채널 중에 Web 이 있습니다. LangChain과 LLM 모델을 사용해서 텍스트를 생성할 때 Web URL 로 부터 데이터를 로드해서 Context 정보로 LLM 모델에 제공하여 이를 참조해 최종 답변을 생성하게 할 수 있습니다.
요즘에 LLM을 이용한 서비스 중에 보면, 특정 웹 서비스의 최상위 URL을 입력하면 하위 directory의 모든 웹 페이지 데이터를 자동으로 크롤링해와서, 이들 모든 웹페이지의 정보를 참조하여 사용자의 질문에 답변을 생성하는 RAG(Retrieval Augmented Generation) 방법을 적용한 챗봇을 매우 짧은 시간에 편리하게 해주는 만들어주는 서비스가 있습니다. 이런 아이디어를 쉽게 구현할 수 있는 방법이 있습니다.
이번 포스팅에서는 LangChain을 이용하여 특정 Root Directory를 지정해주면 그 밑의 모든 URL에 있는 텍스트 데이터를 로드해서 LLM 모델의 인풋으로 사용할 수 있도록 준비하는 방법을 소개하겠습니다.
먼저, 터미널에서 pip install을 이용해서 필요한 Python 모듈을 설치합니다.
! pip install langchain openai unstructured libmagic python-magic-bin
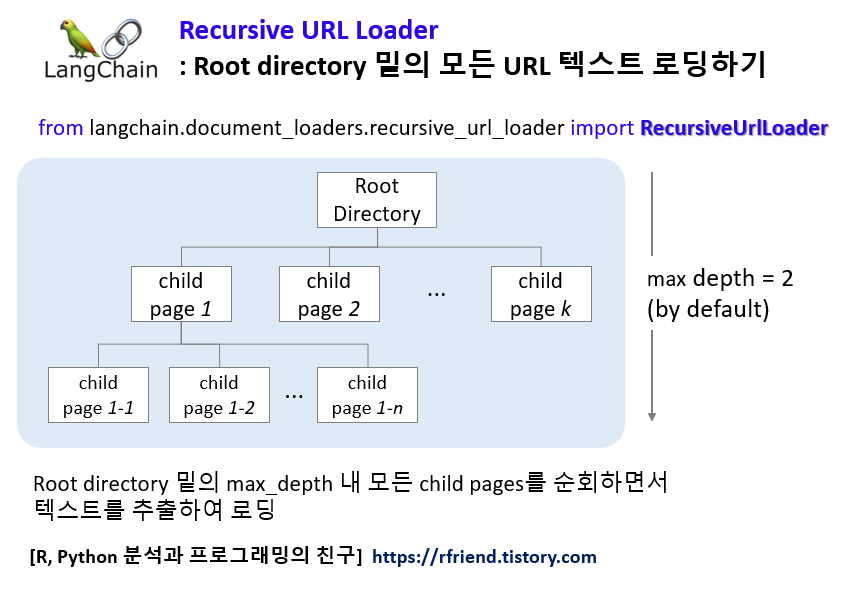
LangChain의 RecursiveUrlLoader 를 이용하면 Root directory 밑의 모든 child pages 에 대해서 자동으로 재귀적으로 (Recursive) 순회하면서 각 웹페이지에 있는 텍스트를 가져와서 로딩해줍니다.
RecursiveUrlLoader 의 'exclude_dirs' 매개변수를 이용하면 제외를 시킬 웹페이지 URL을 별도로 지정해줄 수도 있으니 참고하세요.
BeautifulSoup 의 "html.parser"를 이용하여 HTML tag는 제외한 상태에서 HTML 콘텐츠의 문자열로부터 텍스트를 추출할 수 있습니다.
아래 예제에서는 "https://www.langchain.com/" 페이지와 max_depth=2 까지의 하위 child pages 페이지들로부터 텍스트를 추출하였습니다.
from langchain.document_loaders.recursive_url_loader import RecursiveUrlLoader
from bs4 import BeautifulSoup as Soup
url = "https://www.langchain.com/"
loader = RecursiveUrlLoader(
url=url,
# the maximum depth to crawl, by default 2.
# If you need to crawl the whole website, set it to a number that is large enough would simply do the job.
max_depth=2,
# extract plain text from a string of HTML content, without any HTML tags.
extractor=lambda x: Soup(x, "html.parser").text
)
docs = loader.load()
LangChain의 메인 웹 페이지에서 총 7개 페이지로부터 텍스트를 추출해서 로드했습니다.
len(docs)
# 7
모든 child pages 의 웹페이지를 순회를 하면서 텍스트를 추출해서 로드할 때 (a) page content, (b) metadata 를 가져옵니다. 그리고 각각에 대해서 접근해서 확인해 볼 수 있습니다.
(a) Page Content
docs[0].page_content[:200]
# '\n\n\n\n\nLangChain\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\nð\x9f¦\x9cð\x9f\x94\x97
# LangChainLangSmithLangServeAgentsRetrievalEvaluationBlogDocsPartnersð\x9f¦\x9cð\x9f\x94
# \x97 LangChainð\x9f¦\x9cð\x9f\x94\x97
# LangChain
# Catch up on the latest in LangSmith on YouTube.Bui'
(b) Metadata
docs[0].metadata
# {'source': 'https://www.langchain.com/',
# 'title': 'LangChain',
# 'description': 'LangChainâ\x80\x99s flexible abstractions and extensive toolkit unlocks developers to build context-aware, reasoning LLM applications.',
# 'language': 'en'}
docs[1].metadata
# {'source': 'https://www.langchain.com/langserve',
# 'title': 'LangServe',
# 'description': 'Deploy your LLM application with confidence. LangServe lets you deploy LangChain runnables and chains as a REST API.',
# 'language': 'en'}
docs[2].metadata
# {'source': 'https://www.langchain.com/use-case/agents',
# 'title': 'LangChain Agents',
# 'description': 'Turn your LLMs into reasoning engines.',
# 'language': 'en'}
docs[3].metadata
# {'source': 'https://www.langchain.com/use-case/retrieval',
# 'title': 'Retrieval',
# 'description': 'Personalize and Contextualize your LLM Application.',
# 'language': 'en'}
[ Reference ]
* LangChain - Recursive URL:
https://python.langchain.com/docs/integrations/document_loaders/recursive_url
이번 포스팅이 많은 도움이 되었기를 바랍니다.
행복한 데이터 과학자 되세요!

'Deep Learning (TF, Keras, PyTorch) > Natural Language Processing' 카테고리의 다른 글
| 언어모델 평가 지표 Perplexity 란 무엇인가? (0) | 2024.01.30 |
|---|---|
| [LangChain] pdf 파일과 대화기록을 참조하여 ChatGPT로 질의응답하기 (0) | 2024.01.14 |
| [LangChain] OpenAI Chat Model 의 인풋 메시지, 프롬프트 (0) | 2024.01.08 |
| [LangChain] get_openai_callback() 을 이용해서 OpenAI API 토큰 사용 트래킹하기 (Track token usage for specific calls for the OpenAI API) (0) | 2024.01.07 |
| [LangChain] 캐시를 이용한 응답 속도 향상과 계산 부하 감소 (Caching in LangChain) (0) | 2024.01.07 |



